10　電流が作る磁場： 　　　アンペールの法則とフレミングの左手の法則
f-denshi.com  ［目次へ］　最終更新日：03/05/19

１．アンペールの法則

［１］ ビオサバールの法則からアンペールの法則が導かれます。

アンペールの法則   ［積分形］ 　空間内の任意のループ C ［単一閉曲線］上の磁場 H に関する線積分は，ループ C を縁とする曲面を正方向に通過する正味の電流 I に等しい。すなわち， H ･ds ＝ I　　 特に右図の場合， 　　　　　　[A] の場合の線積分＝0， 　　　　　　[B] の場合の線積分＝I　 となる。( ただし，電流Iの向きが反対の負方向に通過するときは - I 。) ［微分形］ 　電流密度をj　とすると， rot H ＝ j ［変位電流[#]まで考慮した拡張形］ rot H　＝  j ＋ ∂D 　＝j ＋ ∂ε0E  ＋ jp　　　；　j p ＝ ∂P ∂t ∂t ∂t

［積分形の証明 ］　ビオサバールの法則から導きます。

　記号の混乱を防ぐために右図のように上の「アンペールの法則」における，任意の空間内の線積分経路の微分量を
　　　　　　ds　→　du　　
と書き直して説明します。( ds は前章と同じく，電流ループに沿う微分量に使います。)
すなわち，

アンペールの法則：

H ･ du ＝ I

という記号の下で証明します。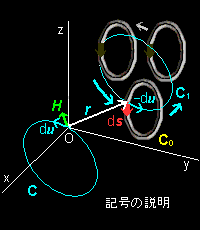

［２］　右図のように座標をとるとき，電流ループ C₀ の微小部分 ds が原点Oに作る磁場 dH は，ビオサバールの法則[#]において，　r　→　−r　として，

dH ＝	I ds×(−r　)
	4πr3

と書けます。したがって，電流ループC₀全体が原点O　に作る磁場は，C₀上の線積分，

H ＝		I ds ×(−r　)
		4πr3

を計算することで求まります。すなわち，アンペールの法則の左辺の閉曲線Cにそった線積分は，

	H ･du ＝				I ds ×(−r )		･du   　　　　　　　　　　　　　　　　　･････　[*]
					4πr3

となります。

［３］　ここからさらに計算を進めるためには，ちょっとしたテクニックが必要なんですが，ループ C₀ の作り出す磁場を考えるとき，

　　　「 空間の点 O から du だけ離れた位置 du に電流ループ C₀ が作り出す磁場 」
と
　　　「電流ループ C₀ を−du だけ移動させた後に電流ループ C₀ が原点 O に作る磁場 」

は等しいことを利用します。つまり，定義どおりにループ Cに沿って移動しながらH の線積分を計算する代わりに，Cと正反対の軌跡を持つループC₁に沿って(図参照)電流ループC₀を動かしながら原点O にできる磁場を積分することも同じであることを利用するのです。

そのためには線積分 [*] の積分範囲，積分変数を

　C → C₁， du  →−du　

と読み替えて，

	H ･du ＝	I				ds ×(-r )	･(-du )
		4π				r3

を計算すればよいことがわかります。　なお，２回でてくるマイナス符号はこれ以降，キャンセルしてしまいましょう。

［４］　この式をよく見ると，［      ］の部分は電流ループ C₀ が du だけ移動したときの原点O から見たC₀ の張る立体角の変化 ，

dΩ＝		ds×r	･(du)
		r3

に等しいことに気がつきます。　なお，立体角については「ベクトル解析」を勉強してください⇒[#]。　これを用いると，

H ･du＝ I dΩ      ･･･[**] 4π

と書くことができます。

［５］　結局，問題はループ C₁に沿った立体角の積分計算に帰結されたわけです。ここで電流ループC₀とループC上の点Oの相対的な位置の変化は，電流ループをC₁に沿って動かす場合も点OをCに沿って動かしても同じであることは先ほど述べたとおりです。

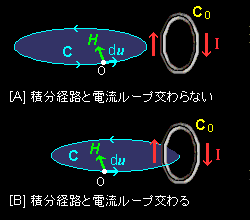
　[**]の右辺の値は，C₁にそってちょうど一周するとき，すなわち，Cに沿って点OがC上を一周するとき，

[A]  その点Oの軌跡が電流ループC₀ を貫いていなければ，立体角の積分は 0 ，すなわち，

	H ･ du ＝ 0

となります。一方，

[B]  電流ループの張る面を正方向に貫くように軌跡 が交わっていれば，立体角の積分値は4πなので[#]，

	H ･du ＝ I

ここでも立体角の計算はベクトル解析[#]を参考にしてください。

［微分形］の証明

［６］　ストークスの定理より，ループ C が作る任意の曲面Sの面積ベクトルをdSとするとき，

	H ･ ds　＝		rotH ･dS

が成り立ちます。一方，ループC の張る曲面を貫く全電流 Ｉ を電流密度　j　を用いて書き直せば，

I ＝		j ･dS

したがって，アンペールの法則は，

	rotH ･dS　＝		j ･dS

と書き直すことができます。そして，この関係が任意の曲面Sについて成り立つので，

rotH  ＝ j

でなければなりません。

２．フレミングの左手の法則

実は，フレミングの左手の法則についての説明は既に済んでいます。これをおさらいした後で，フレミングの左手の法則が，電磁気学に現れる物理量の中でもっとも最初に定義される単位である ”アンペア[A]” の定義にどうかかわっているのか説明します。

［１］　距離r のところに平行におかれた導線0と導線1に電流が流れているとき，どのような力がこの２本の導線の間に働くのか考察します。　8〜9章 [#] で見たように速度 v で運動する電荷 Q が磁場 H₀ から受ける力は，

F　＝ μ₀Qv ×H₀　

となりますが，ここで Qv を導線１に流れる電流微小要素　I₁ds₁ とみなして置き換えれば，

dF₁ (親指)＝ μ₀ I₁ds ₁ (中指) × H₀ (人差し指) 　　 ←　もちろん左手で，･･･

と書けます。これはフレミングの左手の法則そのものです。

［２］　一方， H₀ がビオサバールの法則によって導線０に流れる電流の微小要素　I₀ ds₀ が作る[#]がつくる磁場，

dH0 ＝	I0 ds0 ×r
	4πr3

の重ね合わせ，∫dH₀　で得られるときは，これをH₀ の代わりに用いて，

dF 1 ＝(μ0I1)ds1×		dH0 ＝		μ0 I0 I1	ds1×(ds0×r )
					4πr3

が得られます。この積分の中身に着目すると，これは導線１の電流要素　I₁ds₁( ＝Qv ) が導線０の流れる電流要素 I₀ ds₀ の作る微小磁場 dH₀ から受ける力とみなすことができます。これを2次の微分量として，

d2F 1　＝( μ0I1 ) ds1×dH0 ＝μ0 I0 I1 ･	ds1×(ds0×r )	･･･　[***]
	4πr3

と書くことができます。もちろん，反作用としてのd²F ₀も存在して，

d2F 0　＝ ( μ0I0 ) ds0 × dH1 ＝ μ0I0 I1 ･	ds0×(ds1×r )
	4πr3

と記述できます。(記号の意味は右図を参照してください。)　これから磁力とは，

2つの電流要素　I0ds0 と I1ds1　とに働く磁力 ＝μ0 I1ds1×( I0ds0×r ) 4πr3

とみなすことができ，この様子はしばしば，

2つの電荷　Q0 と Q1 とに働くクーロン力 ＝	1	Q0･Q1･r
	ε0	4πr 3

と対比させられます。これはE-B対応と呼ばれる電磁気学の体系化のよりどころでもあります。

［３］　また，この式は電流の単位，アンペア［Ａ］の定義に使われます。

すると，上の式[***]において，それぞれの導線 1m にわたって積分した値 ( I₀ ＝I₁＝| ds₁|＝|ds₀|＝|r |＝1)， μ₀/4πを 10^-7 に等しいと置くことで，真空中の透磁率は，

μ₀ ＝ 4π×10^-7　＝ 1.256637061×10^-6 ［Hm^-1］

とただちに計算されます。そのようなワケで真空の透磁率はきりのいい数値，4π×10^-7　になっているのです。

これを基にして，１ [A] の電流が流れている導線の断面を１秒間に通過する電荷量（電気量）を１[C] と定めます（電荷量の定義）。さらに，真空中に2つの1[C] の電荷を 1m 離しておき，この電荷間に働く力の大きさの側定値　f　[N］ ＝ 1/(4πε₀) から，誘電率ε₀を計算して求めることができるはずです[#]。しかし，実際はより精度の高い値の得られる光速度 c ＝ 2.99792458×10⁸　[m/s] を用いて，

ε₀ ＝1 / ( μ₀c²)

なる関係[#] より，ε₀ が算出されます。ちなみに，

f　＝ 8.9878･･･×109　       ［N］ ε0 ＝ 8.854187817･･･×10-12　［F/m］

電磁気学の理論体系における真空の誘電率 ε₀ は，クーロンの法則とともに最初に現れる物理定数ですが，実験的にはかなり従属的な量と言えます。

［ 目次へ ］

CopyRight　フジエダ電子出版