| 2 クーロンの法則 | ||
| f-denshi.com [目次へ ] 最終更新日:04/02/25 | ||
| サイト検索 | ||
[1] 粒子(物質)間に働く力の一つを説明するために,「粒子は電荷と呼ばれる保存量をもつ」ことがあると無条件で受け入れることにします。原子や分子の相互作用やその再配列を扱う化学の範囲では,原子核をプラス電荷の起源,電子をマイナス電荷の起源とすることができます。電子1個の持つ電荷が電荷の最小単位(=電荷素量という)で,物質の持つ電荷はゼロを含めてすべてこの整数倍になっていることも知られています。
このような電荷を帯びた2つの静止している粒子間に働く力と電荷との関係は実験事実に基づいて,次のクーロンの法則 (Coulomb Law) として述べることができます。
|
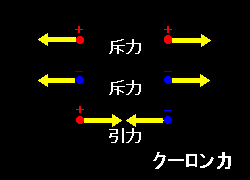 |
静電荷の間には力学の作用・反作用の法則も同時に成り立ちます。すなわち,それぞれの粒子が受ける力は大きさが同じで,方向が反対になっています。
[2] また,MKSA単位系で比例定数 k は,
k ≡ 1 4πε
と置き換えられます(有理系)。ここでεは誘電率(単位は[F/m])と呼ばれ,2つの電荷の間を満たしている物質(真空状態も含む)で決まる定数 (異方性のある物質中ではテンソル) です。このように比例定数に 4π を含ませて定義するのは,そうすることでマックスウェル方程式[#]をはじめとする基礎方程式において 4π という余分な係数が現れないからです[#]。ただし,球対称性のないビオ・サバールの法則[#]は例外です。
[3] また,電荷の単位はクーロン [C] を用います。MKSA単位系では電流の方がより基本的な単位で,まず電流の単位 [A]が定義され[#],それに基づいて電荷 [C] が次のように定義されます。
| 電荷の定義: ある断面を横切って1[A ]の電流が流れるとき,その断面を1秒間に横切る電荷を1[C ]と定める。 ( 単位: [C]=[A・s] ) |
一方,真空中の誘電率の単位は,
ε0=8.854187817×10-12 [C2/(Nm2)]=[C/(Vm)]=[F/m] ⇒ [#]
ですが,これも透磁率[#1],[#2] と光速度から求められるものです。
これらの数値を用いて,1[C]の電荷を1m離して置いたときに働く力は 8.9878×109 [N ] となります。(注意)
[4] クーロンの法則をベクトルを用いて表します。
|
クーロンの法則 [電場表現 ] 原点におかれた電荷 Q をもつ粒子0が位置 r にある電荷 q を持つ粒子1に及ぼす力は,
となる。特に粒子1の電荷 q 以外の部分をまとめて
と書き,E を電荷 Q をもつ粒子 0 が位置r に作る電場,または電界という。 すると,粒子1の受ける力は,
と書ける。 |
このように電場という物理量を導入することには,単に記号の省略や置き換えが目的ではなく,この表現には近接相互作用と呼ばれる概念が背後に存在しています。これは電荷が電荷に直接力が働くと考えるのではなく,
(1) 電荷が存在するまわりに電場と呼ばれる空間の”ひずみ”のようなものを作りだす。
(2) 電場の中にある電荷には力が働く
という考え方です。つまり,電荷は電場を生成し,その電場を介して電荷は力を受けます。実際,この考え方には正当性があり,電荷の状態変化 (振動など) は電場の変化として空間を有限速度,すなわち,光速度で伝わることが知られています[#]。
一方,力学の作用反作用の法則に従い,粒子0は,粒子1から F とは正反対の力 −F を受けます。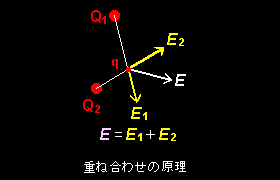
[5] また,電荷間に働く力には重ね合わせの原理が成り立ちます。(数学的にはE をベクトル空間 [#]の元 (=ベクトル) として扱うことが可能ということです。ここでは,重ね合わせの原理はクーロンの法則に含めることにし,「クーロンの法則」を引用するときは重ね合わせの原理も成り立つこととします。)
これの意味することは,電荷が多数存在しているときでもクーロンの法則がすべての電荷どおしの間でそれぞれ独立して成り立つということです。たとえば,右図のように3つの荷電粒子がある場合,
| 電荷q が受ける力は電荷Q1から受ける力と電荷Q2から受ける力の和(ベクトル和)である。 |
というものです。式で書くと,
| F =kqQ1・ | r1 | +kqQ2・ | r2 | = qE1+qE2 = q(E1+E2 ) |
| |r 1| 3 | |r 2| 3 |
最後の = から,「電荷Q1がある位置に作る電場 E1 と,電荷 Q2 がその位置に作る電場 E2 の和がその位置の電場 E=E1+E2 となる。」ということです。 電場という概念を導入すると,ある位置 の電場E を知ることで,その発生源がどうであれ,その位置に置かれた電荷q は力
F = qE
を受けるとして取り扱うことができるのです。 この式から電場の大きさ |E | の単位は,[N/C]であることがわかりますが,後に電圧(電位)を導入すると,[V/m]とも書き直せることが示せます [#]。
[5] なお,電荷が巨視的に見て連続的に分布しているときは,位置s における電荷密度ρ(s) を用いて次のように表されます。
E (r ) = 1 ρ(s )(r−s ) d3s 4πε |r −s | 3
[1] 電場の向き,大きさを視覚的に表すために電気力線が有効に使われます。
定義は次のようになります。
電気力線の定義:
1.電気力線の各点での接線はその点での電場の向き。
2.電気力線の始点は正電荷,終点は負電荷,またはどちらかが無限遠。
3.電気力線の密度(本/m2)は電場の強さ|E|に比例する。
4.正電荷Q からは(Q/ε)本の電気力線が発生する。
(負電荷 -Q においてQ/ε本の電気力線が消滅する。)
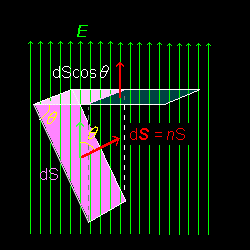
以上の約束の下では,電場E に置かれた微小面積(面積素ベクトル[#] を dS とする)を貫く電気力線の本数は内積:
E ・ dS =|E|dS cosθ (電場に垂直な面に換算)
で与えられることがわかります。(下図参照)
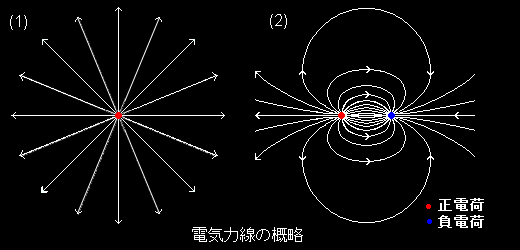
[2] 電気力線の具体例として,
(1) 正電荷Q から発生して,無限遠で消滅する電気力線
(2) 正電荷Q から発生して,負電荷-Qで消滅する電気力線
の様子(断面図)を下図に描いています。
電場 E : [N]/[C] [V]=[J/C]=[(Nm)/C] より E :[V]/[m] とも書ける。
(注意)cgs単位系では等量の電荷を1cm離して置いたときに働く力が1[dyn]のとき,その電荷を1[esu]と決めます。