| 8 磁場:運動の相対性からの要請 | ||
| f-denshi.com [目次へ] 最終更新日: 21/10/20 | ||
| サイト検索 | ||
このページを読めば,なぜ,理論物理学では「4つの力」という言い方がされるのか理解できます。
この世界・宇宙に存在する力(相互作用)は,(1)重力,(2)強い相互作用,(3)弱い相互作用,そして(4)電磁気力の4つと言われます。なぜ,クーロン力と磁力との2つに分けず,電磁気力と一括りにするのでしょうか。
電流が作る磁場に関する諸法則は,歴史的には実験事実として確立されてきました。このような法則にはビオ・サバールの法則,アンペールの法則,フレミングの左手の法則などがあります。しかし,現代的な知見に基づけば,これらの諸法則は電荷のクーロンの法則さえ認めれば,時間,空間の対称性(=特殊相対性理論)と電荷保存の法則から必然的な帰結として得ることができます。この講義ではこの立場からまず,磁力の存在を導き出してみましょう。
 特殊相対性原理に基づけば,互いに等速直線運動する任意の座標系(=慣性系)において物理法則は等価でなければいけません。電磁気学の法則も例外であってはいけません。「ある座標系で観測したときに荷電粒子に力が働いているにもかかわらず,別の座標系で観測すると力は働いていない」というようなことが起こってはならないのです。
特殊相対性原理に基づけば,互いに等速直線運動する任意の座標系(=慣性系)において物理法則は等価でなければいけません。電磁気学の法則も例外であってはいけません。「ある座標系で観測したときに荷電粒子に力が働いているにもかかわらず,別の座標系で観測すると力は働いていない」というようなことが起こってはならないのです。
そこで,クーロンの法則がすべての慣性系で成立するならば,どのようなことが起きるのか考えます。
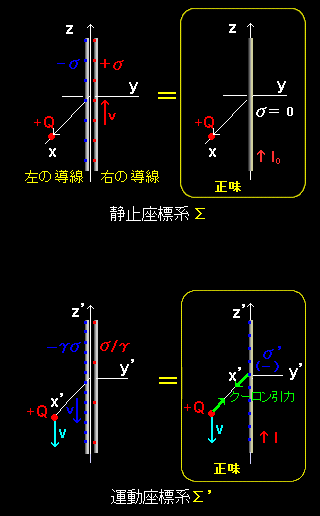
[1] 静止座標系Σ において,無限と見なせるほど長い静止した導線(左の導線)と速度 v で z 方向に等速運動する導線(右の導線)が小さな距離δ離れて平行に配置されている状況を考えます。
導線の持つ線電荷密度が静止座標系でそれぞれ−σ(左側),+σ(右)であるならば,この2本の導線の作る電場は導線から遠い場所ではお互い打ち消し合いゼロとなります。また,右の導線は速度v
の運動により電流 I0 が+z方向に流れているように見えます。
したがって,導線から r >> δ の距離に静止している点電荷 Q
には電気的な力が働くことはありません。
[2] 次に同じ現象を座標系Σ に対し,+z 方向(上向き)に速度 v で運動する座標系Σ 'から観察して見ましょう。この場合,点電荷 Q とマイナス電荷帯びた導線(左)は速度 v で −z 方向 (下向き) に等速直線運動して見えるはずです。(つまり,左の導線は+z 方向にプラスの電流が流れているのと同じ) 一方,プラス電荷を帯びた導線(右)は静止して見えるはずです。
また,この座標変換によって,導線(のz方向の長さ)はローレンツ変換(左の導線),または逆変換(右の導線)[#]を受けますから,
(1) 導線(左)は z 方向に縮小し,
(2) 導線(右)は z 方向に伸張する
ことが観察されます。ここで,すべての座標系で電荷が保存する(電荷保存の法則)と仮定すれば[#],各導線の線電荷密度等は,
γ = 1
1−(v/c)2
として,
| [静止座標系Σ] | ⇒ | [運動座標系Σ '] | ||
| 線電荷密度(左) | −σ [静止] | ⇒ | −γσ [−v] | |
| 線電荷密度(右): | +σ [+v] | ⇒ | σ/γ [静止] | |
| 線電荷密度(合計): | 0 | ⇒ | σ ' = σ(γ-1−γ) = −σγ(v/c)2 < 0 |
|
| 電流(合計): | I0 =σv | ⇒ |
|
|
と変化します。 (電荷を含む長さ(体積)は変化しても電荷量は変化しないという仮定で電荷密度を計算しています。)
[2.5] つまり,運動座標系Σ 'で,十分遠方からこれらの導線を見ると,正味でマイナスの電荷密度σ’が存在しているように見えます(←そのように近似計算ができるということ。)このため,導線から R の位置には3章で計算したように[#]大きさが次のような電場 ( x 成分 ),
E ’ = σ ' = -( σγ v)v (x成分) 2πε0R 2πε0Rc2
= - v I = - μ0 v I 2πRε0c2 2πR
が生じ,運動座標系Σ 'ではx軸上の点電荷 +Q には導線に向かってクーロンの法則に従う引力,F'=QE' が働くことになってしまいます。
1/(ε0c2) → μ0 という置き換えを行ないました。
(注意: もちろん,この μ0 は単なる記号の置き換えの産物ではなく,
後に真空中の透磁率と呼ばれることになる重要な物理定数[#]です。)
[3] この考察結果のままでは,この引力のために
「静止座標系Σでは力が働かずに静止して見える荷電粒子 Q を運動座標系 Σ ' で観測すると,粒子が導線に向かって引力を受けて加速度運動をする 。」
ことになり,特殊相対性原理に基づいて期待される,
「互いに等速直線運動するすべて座標系からこの粒子は等速直線運動するように見える。」
を満足しません。(ここでいう等速直線運動には静止も含みます。)
この矛盾を解決するためには,クーロンの法則に付随して次の法則,
「電流と反平行に運動する電荷には上で計算された力をキャンセルするような力(斥力)が発生する。」
(↑ とりあえず,いまのところの表現です。)
を導入する必要があります。
”理論物理学者風” にカッコ良く言い回すならば,「 特殊相対性理論の要請(時空の対称性)によって,クーロン相互作用にはペアとなるべきもうひとつ新しい相互作用が存在しなければならない。」とでもいうところでしょうか?
そして,その大きさは,
F = Qvμ0 I [ N ] (斥力) ・・・・・ [*] 2πR
で,方向はx 軸正方向 でなければなりません。
[4] すると,運動座標系 Σ ' でも粒子 Q には先に計算したクーロン力 ( [2]の結論 ) とこの新しい力がつり合って,正味の力が働かないため,「粒子は速度−v で直線運動する。」ことが観察され,特殊相対性原理が成り立ちます。この予想される ”新しい力” を磁力と呼びます。
また,μ0 の単位は[*] 式から逆算すれば,
| [μ0]= | [N][m] | =[N][A]-2 ( =[V][s][A・m]-1 ) |
| [C][m/s][A] |
 ですが,[H・m-1]とも表記されます。 [H ]:ヘンリー については,⇒ こちら
ですが,[H・m-1]とも表記されます。 [H ]:ヘンリー については,⇒ こちら
[C] = [A][s] でしたね。[#]
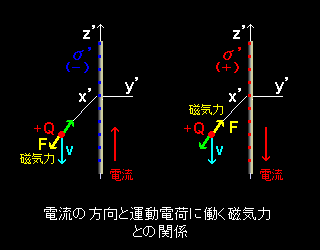
[5] さて,以上のような磁力を導き出すための考察は,最初の2本の導線の電荷密度 [#] の符号を交換して行なうこともできます。そのとき,運動座標系で観測される導線の正味の電流は先程とは反対で - z方向,また,2本の導線合わせた合計の電荷密度も|σ’|=σ’ > 0 と反対符号となり,導線と電荷 Q との間にはクーロン斥力が発生することになります。そして,この力を打ち消すために導入すべき法則は,
「電流と ”平行” に運動する電荷には ”引力” が発生する。」
となります。もちろん,力の大きさは先程 [*] と同じです。
F = Qvμ0 I [ N ] (引力) 2πR
[1] クーロンの法則において,電荷Qに働く力を説明するとき,F = QE と表せるように電場 E を導入したように,電流が速度v 運動する電荷Qに力を及ぼす場,つまり,磁場と呼ばれる量H を導入しましょう。
まず,上の考察において導かれた磁力 [*]に対応する磁場の定義において,大きさだけについていえば,磁場H の中で速度 v で運動する電荷 Q が受ける力の大きさが, F = ( μ0Qv ) H と記述できると好都合です。そのためには,H を,
|
≡ μ0Qv ・ H すなわち ⇒ |
|
と定義する必要があります。 ( E-H 対応 )
[2] 一方,磁場H はベクトル場で,各点でのH の方向が電流ベクトルI によって一意的に定まり (I の一価関数),さらに電荷 Q の運動速度 v が与えられたとき,一意的に力のベクトルF を計算できる必要もあります。さらに空間対称性から,
(1) z 成分を持たない → xy平面内のベクトル場
(2) 電流の向きの反転で力の向きが反転 ⇒ 磁場の向きが反転する[#]
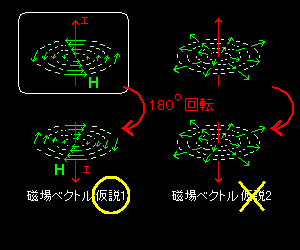
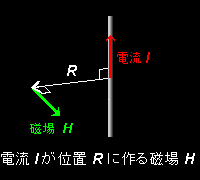
必要もあることから,下図の仮説 1 のよう動径方向に垂直な方向(成分)を磁場ベクトルの方向として採用できることがわかります。また,動径方向に垂直な方向は2方向考えられますが,慣用でI とH の関係がいわゆる右ねじの方向になるようにH の方向が選ばれます。
 |
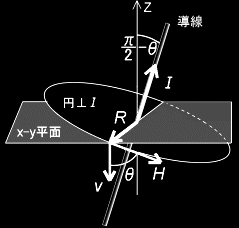 |
導線の方向が z 方向と θ’の角をなす一般の場合は,導線のz軸への射影成分 についてのローレンツ収縮を考察すればよく,それは,H とv とのなす角度θ(=π/2-θ’)を用いると (上図右参照 ←09/04/28追加),cos(π/2-θ)=sinθを先程の結果に乗じることになり,ベクトルの外積[#]を用いて表記すると,
 |
 |
H = I × (R / R ) = I × R 2πR 2πR2
とあらわすことができます。
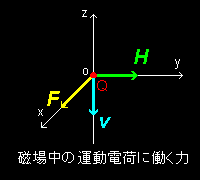
[3] 力の方向も考慮すると,結局,ローレンツ力と呼ばれる磁場の中を運動する電荷に働く力 F =μ0Qv H は,
F = Qv × (μ0H )
= Qv × B
となります。ここで,
B=μ0H [V・s・m-2] (=[Wb・m-2]=[T])
とおきました。このB を磁気誘導,または磁束密度と呼びます。
↑ 単位 [Wb] については磁荷の単位[#]のところで説明します。
最後のベクトルの外積 × を導入するところはかなり,天下り的に書いてしまいましたが,代数的な一意性の吟味などは,物理のかぎしっぽのJohさんの記事「七次元の外積」などその周辺の記事が参考になります。
このように,電荷が静止していない慣性系でもクーロンの法則を成立させようとすると,新しい力を導入する必要性が生じてきます。ただし,「新しい力(相互作用)」 とはいっても,異なる慣性系を採用したことによって,クーロン力をより普遍性のあるものにするための修正の範囲であることは,ここでの磁力の導出過程からわかりますね。
つまり,電荷の間に働く”一つの力”を様々な慣性系で記述するための方便として,クーロン力と磁力(ローレンツ力)という ”2つの成分” に分けて整理したものが,19世紀の現象論としての電磁気学の姿なわけです。
したがって,クーロンの法則とは,電荷が静止して見える”特別な”慣性座標系においてのみ適用な可能な「電磁気力」の”特別な”表現に過ぎないのです。それで,理論物理学では,クーロン力と磁力とを異なる2つの力としては数えないのです。
一般的に,電場と磁場が慣性系どおしの間で,どのように(ローレンツ)変換され,混じり合うかはこちらにまとめています。 ⇒ [#]
μ0 [N][A]-2 (=[H・m-1]) [N]=[C][V][m]-1=[A][s][V][m]-1
H [ A ・m-1 ]
B [V・s・m-2] ← (=[Wb・m-2])