| 7 面積分と立体角 | |
| f-denshi.com [目次へ] 最終更新日:03/05/13 | |
| サイト検索 | |
[定義]
[1] 3次元ユークリッド空間の領域D上のベクトル関数 A(x,y,z) = (A1,A2,A3) が C1級関数[#]:
A1 = A1(x,y,z), A2 = A2(x,y,z), A3 = A3(x,y,z)
として与えられているとします。
[2] このとき,ベクトル方程式 r(u,v) で表されるD 内の曲面 S[#]:
r(u,v) = (x(u,v),y(u,v),z(u,v)); a≦u≦b , c≦v≦d
上のベクトルA の面積分を次のように定義します。↓形式的でちょっとつまらないけどガマン
[3] まず,曲面上の点(x,y,z) は媒介変数 u,v を用いて表わされ,
A =(A1(x(u,v),y(u,v),z(u,v)),A2(x(u,v),y(u,v),z(u,v)], A3(x(u,v),y(u,v),z(u,v)))
=(A1(u,v),A2(u,v),A3(u,v))
=A(u,v)
のように書けることを確認しておきます[#]。次に,
[4] D に対応する (u,v) の領域 U について, u の区間 [a,b]を m 個の区間,v の区間 [c,d]を n個の区間:
[a=u0,u1],(u1,u2],・・・(uj-1,uj],・・・,(um-1,b=um]
[c=v0,v1],(v1,v2],・・・(vk-1,vk],・・・,(vn-1,c=vn]
に分割することでUを細分化します。また,次の記号を導入します。
Δuj =uj−uj-1 ; uj-1<uj≦uj
Δvk =vk−vk-1 ; vk-1<vk≦vk
h =Max( Δuj ,Δvk ), ただし,j=1,2,・・・,m ; k=1,2,・・・,n
[5] ここで,微小面積 ΔujΔvkにこの微小面内の点の (uj,vk) におけるベクトルA とベクトル {r u(uj,vk)×r v(uj,vk)} との内積を乗じたものをすべての微小面積素片について総和し,その値のh→0 における極限 (もちろん,m と n は∞にいきます),すなわち,
{A (x(uj,vk),y(uj,vk),z(uj,vk))・(r u(uj,vk)×r v(uj,vk))}ΔujΔvk
を次のような記号で書いて,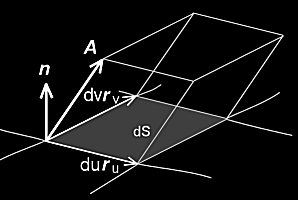
⇔ A(u,v)・(ru×rv)dudv
ベクトルA の面積分といいます。また,ベクトルA の束という言い方もされます。(右図平行6面体の符号付体積の総和,2009/12/26図差し替え)
この定義で,外積(ru×rv)が乗じられている理由は,4-1章で述べた[#]ように2つのパラメータ u,v で表される曲面の位置 r =[x(u,v),y(u,v),z(u,v)]における微小面積 dS と法線 n との積が,
ndS =(r u×r v)dudv
n = ru×rv |ru×rv|
で与えられることを反映してのことです。
このような積分を定義することで,例えば,ベクトルA (x(u,v),y(u,v),z(u,v))が流体の速度を表すとき,この面積分を計算することでこの曲面を通過する流体の量 (= 右図のような斜方柱の体積 A・ndS の総和 ) を簡明に表現することができるようになります。
[6] 以下,具体的な(問題に応じた)計算に役立つ面積分のいろいろな表現を列挙しておきます。
|
(1) ru×rv=[J(yz/uv),J(zx/uv),J(xy/uv)]を用いる[#]と,
(2) ユークリッド空間(xyz変数)での積分に書き直すと,
ここで,dS に関しては4-2章の記法[#]を用いてます。 (3) 単位法線ベクトル n = (cosα,cosβ,cosγ) がわかっているときはさらに,
右図を参考にしてください。 |
[7] 特別な場合として,半径R(一定)の球面上でのベクトルの面積分であるならば,球座標を利用して,
I = A(θ,φ)・n |rθ×rφ|dφdθ
を計算します。ここで,
r(θ,φ) = (x(θ,φ),y(θ,φ),z(θ,φ)) ←座標原点を球の中心に定めて
x(θ,φ) = R sinθcosφ,
y(θ,φ) = R sinθsinφ,
z(θ,φ) = R cosθ
J(yz/θφ)=R2sin2θcosφ
J(zx/θφ)=R2sin2θsinφ
J(xy/θφ)=R2sinθcosθ
|rθ×rφ|=R2sinθ
および,
A(θ,φ)=A1(θ,φ)er+A2(θ,φ)eθ+A3(θ,φ)eφ
n=er
であることに注意すれば,
I = A1(θ,φ) R2sinθ dφdθ
と簡潔になります。
| φ( x(u,v),y(u,v),z(u,v) ) | ∂r | × | ∂r | dudv | ||||||
| ∂u | ∂v |
φ=1 のときは,この積分値は曲面積Sと等しくなります。
スカラー関数φ=1の線積分についてはこちら ⇒ [#]
「回転定理」を参照⇒[#]
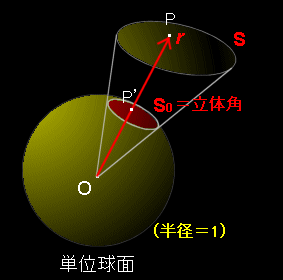
[1] 立体角の厳密な定義は面積分を用いて与えられます。
基点(原点)O から有界な曲面 S の1点 P を指す位置ベクトルr とします。このとき,
Ω ≡ r・dS ⇔ dΩ ≡ r ・dS r3 r3
で定義される Ωを原点O から見た 曲面S の立体角といいます。ここで,曲面 S には向きが指定されている必要があり,dS とは曲面の正方向に垂直な面積素ベクトルです[#]。
[2] 立体角の幾何学的な意味は,折り返しのないような最も簡単な場合,線分 OP と原点O に中心を持つ半径1の球面(単位球面)と交点P’を考えると,P がS 全体を動くときに対応する点P’全体が単位球面上に作る面積 S0と考えることができます。(右上図)
( 半径1の球面上の領域に限れば,dΩ=sinθdθdφ [極座標表示] )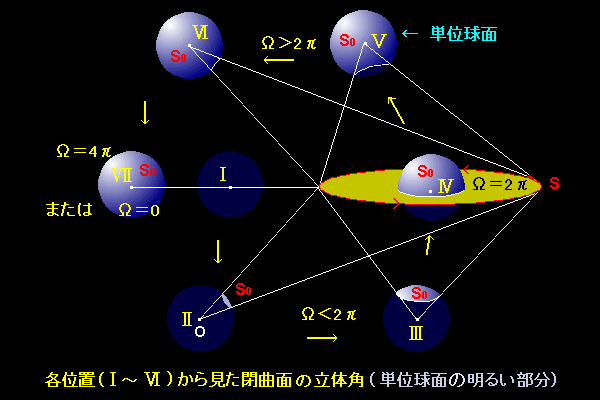
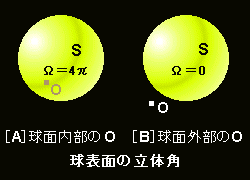
[3] 曲面S が球面のような閉曲面であるとき立体角は,
[A] 原点O が閉曲面の内部にある場合 ⇒ Ω=4π
[B] 原点O が閉曲面の外部にある場合 ⇒ Ω=0
となります。
[B] の値が0 となるのは次のような理由からです。原点O から球面に接線を引いたとき,その接点全体の集合は球面上の円となり,球面S
を2つの領域(S1とS2)に分けます。そしてそれぞれの領域の立体角は絶対値が等しく,符号が逆であることから,その和集合である球面Sの立体角は0
なのです。
[4] 応用上,立体角は最初に述べた定義式とは異なった形で表現し,計算に利用されることがしばしばあります。電磁気学への応用ではむしろこれから述べることの方が重要です。
 |
 |
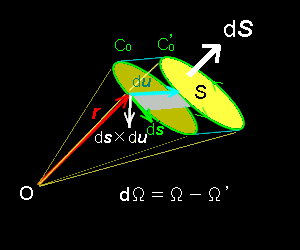
対象となる曲面 S(周囲 C0) を du だけ平行移動させることを考えます。 これに伴い,
周囲: C0 → C0’
と平行移動し,この周囲 C0 の移動の軌跡(体積)は斜方柱の”側面”になります(右図)。
移動にともなう曲面 S の立体角Ωの変化 dΩは,この”側面”の立体角を計算することで求めることができます。
図の銀色で示した微小側面(平行四辺形)について,向き付きの閉曲線C0の接線ベクトルの微分量をdsとして,
面積ベクトル: ds×du
なので,この微小側面の C0 の立体角の増加(正の値)dΩへの寄与は,
−(ds×du)・r r3
で与えられます。
(ここで,マイナスがつく理由は,C0 の移動の軌跡である銀色の側面部分が原点O から見えるならば,dS・r <0 ですが,この変化は曲面Sの立体角の増加(dΩ>0)に寄与するからです。)
[5] したがって,側面全体からの寄与はこれを C0 に沿って積分(変数はds )すれば求められます。これをスカラー3重積の公式[#]を用いて計算し,積分変数 ds と関係ない du を積分の外に出して,
dΩ= −(ds×du)・r = −(r×ds)・du =+du ・ ds×r r3 r3 r3
となります。(電磁気学の著明な法則どおしを結びつけるときの最も重要な公式です。)
また,方向微分係数[#]をベクトル表記した,
dΩ(u)=Ω(u+du)−Ω(u)=gradΩ(u)・du
と比較すれば,
gradΩ(u)= ds×r r3
とも書くことができます。最後の3つの式は電磁気学の基本法則の等価性(立体角を用いてローレンル力の表現方法にバリエーションを付けている)を示すために利用します。
電磁気学(アンペールの法則)への応用例はこちら⇒[#]
電磁気学(ファラデー(-レンツ)の法則)への応用例はこちら⇒[#]
09/12/02 追加
[1] 各種積分の定義を比較すると,理解が深まるかも知れません。
曲線,面積,および,体積の計算の素となる図形を下図に比較として示します。
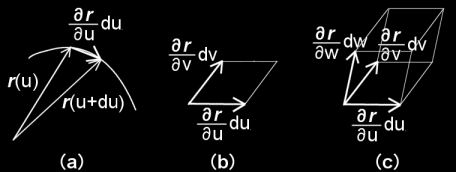
(a) 線密度ρ(u)が与えられる場合,
| 微小線分の方向つき長さ: | ∂r | du ⇒ 曲線の長さ= | ∂r | du | |||||||||||||||
| ∂u | ∂u |
| 曲線の重量= | ρ(u) | ∂r | du | |||||||||
| ∂u |
(b) 面密度ρ(u,v)が与えられる場合
| 微小平行四辺形の方向つき面積: | ∂r | × | ∂r | dudv ⇒ 曲面の面積= | ∂r | × | ∂r | dudv | ||||||||||||
| ∂u | ∂v | ∂u | ∂v | |||||||||||||||||
| 曲面の重量= | ρ(u,v) | ∂r | × | ∂r | dudv | ||||||||
| ∂u | ∂v | ||||||||||||
[2] 以上はここまでに説明済みですが,自然な拡張として線分や平行四辺形を考える代わりに微小な平行六面体の符号つき体積,
∂r ・ ∂r × ∂r dudvdw ∂u ∂v ∂w
を考えると体積計算の素となります。
(c) 体積密度ρ(u,v,w)が与えられる場合
| 微小平行六面体の符号つき体積: | ∂r | ・ | ∂r | × | ∂r | dudvdw ⇒ 曲体?の体積= | ∂r | ・ | ∂r | × | ∂r | dudvdw | |||||||||||||||||||
| ∂u | ∂v | ∂w | ∂u | ∂v | ∂w |
これよりスカラー関数の体積分はスカラー3重積[#]を用いて,
φ(u,v,w) ∂r ・ ∂r × ∂r dudvdw ∂u ∂v ∂w
または,
φ(u,v,w) ∂r ∂r ∂r dudvdw ∂u ∂v ∂w
ただし, ∂r ∂r ∂r = ∂u ∂v ∂w | J (xyz/uvw) | =
∂x ∂u
∂x ∂v
∂x ∂w
∂y ∂u
∂y ∂v
∂y ∂w
∂z ∂u
∂z ∂v
∂z ∂w
で定義します。密度にムラがある立体(3次元の部分空間)の総重量は体積密度ρ(u,v,w)を用いて,
ρ(u,v,w) ∂r ・ ∂r × ∂r dudvdw ∂u ∂v ∂w
で求められることになります。