ときわ台学/ベクトル解析/曲面のベクトル方程式と面積

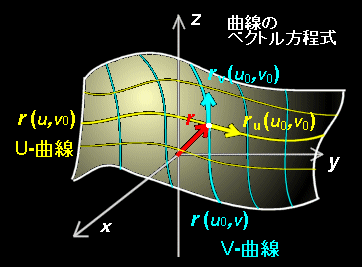
［１］　独立な２つの媒介変数 u，v で表される位置ベクトル

の先端の軌跡は一般に曲面を表します。このベクトルを曲面のベクトル方程式といいます。

［２］　この方程式で u，または v　の一方を定数としたものはこの曲面に埋め込まれている曲線を表し，

［３］　曲面の各点におけるベクトル方程式の u ，または v に関する偏導関数を

と定義します。また，曲面上の点r (u₀,v₀)において，このr_u(u₀,v₀)，r_v(u₀,v₀) が存在するとき，これらの張る２次元ベクトル空間(＝平面)：

［４］　曲面の各点r (u,v)における r_u，r_v の外積 [#]を考えると，

は各点における接平面に垂直なベクトルです。( ←r_u･(r_u×r_v)＝r_v･(r_u×r_v)＝0 なので )　これを規格化した，

を曲面上の点r (u,v)における単位法線ベクトルといいます。｜r_u×r_v｜は２つの接線ベクトルから作られる平行四辺形の面積となります。

ところで，r_u×r_v ＝ 0　となる点（r_uとr_v が1次独立でないとき）では単位法線ベクトルや接平面を定義できませんが，このような点を特異点といいます。そうでない点を正則点といいます。
　これ以後，特に断りのない限り，考えている曲面は特異点を含まないこととし，これをなめらかな曲面と呼ぶことにします。（なめらかな曲面のみをはじめから「曲面」と定義する教科書もある。）

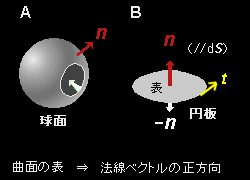
［５］　この単位法線ベクトルの定義だけでは，媒介変数 u と v のどちらかに優先的地位を与える理由がないので，お互い180°反対方向を向いているr_u×r_v　とr_v×r_u　のどちらもn にとることができます。しかし，有界な曲面に対しては以下のように正方向を決める(＝u,v を決める)ことが慣用となっています。　　

［空間座標を媒介変数とする曲面の取り扱い］(つまり，これまでの議論での u→x，v→y の場合です。)

［６］　曲面の方程式が z ＝ z(x,y) と解くことができる「曲面のベクトル方程式」は，

r (x,y) ＝ (x,y,z(x,y))

と書くことができます。すると，r の x,y に関する偏微分とその外積は，

r_x ＝ (1,0,z_x)，r_y ＝ (0,1,z_y)　 ⇒ 　r_x×r_y＝(-z_x,-z_y,1)

となります。そして，

曲面 z ＝ z(x,y) 上の単位法線ベクトル[#]は，

n ＝(n₁，n₂，n₃) ＝ (－z_x/N，－z_y/N，1/N ) ・・・・・・・・・・・　[*]

ただし，　N ＝｜r_x×r_y｜＝((z_x)²＋(z_y)²＋1)^1/2

［７］　曲面を　ψ(x,y,z) ＝ 0　と表すときはその各偏微分を ψ_x，ψ_y，ψ_z とすれば，陰関数定理[#]より，

　z_x＝ ∂z ＝－ ψ_x 　および，　z_y＝ ∂z ＝－ ψ_y

∂x ψ_z ∂y ψ_z

これを上の結果(囲みの部分)　[*]に代入すると，

n ＝ ( ψ_x/ψ_z ,ψ_y/ψ_z , 1 )

｛ (ψ_x/ψ_z)²＋(ψ_y/ψ_z)²＋1 ｝^1/2

＝ ( ψ_x ,ψ_y ,ψ_z )

｛ ψ_x²＋ψ_y²＋ψ_z² ｝^1/2

という対称性の良い式になります。よって，

曲面 ψ(x,y，z) ＝ 0 上の各点での単位法線ベクトルは，

n ＝ (n₁，n₂，n₃) ＝ ψ_x ， ψ_y ， ψ_z ＝ ∇ψ

｜∇ψ｜｜∇ψ｜｜∇ψ｜｜∇ψ｜

ただし，｜∇ψ｜＝((ψ_x)²＋(ψ_y)²＋(ψ_z)²)^1/2　で定義される。

ということができます。

［３次元空間内の曲面の面積］

［８］　z ＝ z(x,y) と解くことができる曲面の面積 S を求める方法(＝合理的な定義)を考えます。曲面 S の各点は xy平面の点と１対1に対応しており，非常に細かく分割したどの微小面積dS の一つ一つを考えても，その xy 平面への正射影 dxdy と，

　　 n･e_z dS ＝ n₃dS ＝ dxdy　

と関係づけられるとします。ここで，e_zはz軸方向の単位ベクトル (0，0，1)です。すると，曲面積 S は，その和として

　S＝ dS ＝ (n₃)^-1 dxdy

　　　＝　｛(z_x)²＋(z_y)²＋1 ｝^1/2 dxdy　　←　[*]　を用いて

と定義することは妥当でしょう。この式は，

dS ＝｛(z_x)²＋(z_y)²＋1｝^1/2 dxdy

［９］　曲面が　ψ(x,y,z) ＝ 0　と表せるときは結果だけ書くと，　←　［７］　の導出を参考 n₃＝ψ_z/｜∇ψ｜ψ_z

dS ＝ ψ_z^-1･｛(ψ_x)²＋(ψ_y)²＋(ψ_z)² ｝^1/2 dxdy

注意：ここでの議論は分割して曲面を，z＝f(x,y) とできる場合にも成り立ちます。また，y＝g(z，x)，x＝h(y，z) と解くことができれば，yz，zx平面への射影を利用しても曲面積の同様な定義が可能です。

［10］　曲面積を求める上の方法を一般化します。
　曲面が媒介変数，u,v　で与えられるときはこの領域 U とユークリッド空間(変数　x-y-z)の領域 S が対応し，

がC¹写像で， J(xy/uv)≠0　ならば，積分変数の変換( x,y → u,v )の公式[#]から

の２式からつくった，
　　　0 ＝(1)×z_v－(2)×z_u
　　　　＝－z_x(z_ux_v－z_vx_u)＋z_y(z_vy_u－z_uy_v)
　　　　＝－z_xJ(zx/uv)＋z_yJ(yz/uv)
と陰関数定理とから得られる比例関係

［12］　結局，r_u×r_v＝(J(yz/uv),J(zx/uv),J(xy/uv))であることを考えると，変数u,v の領域 U と曲面上の領域 S との微分量の関係は，

と書くことができます。また，スカラ－dS と単位法線ベクトルn [#]

との積を次のように形式的なベクトル dS ［微分面積ベクトル］を定義して用います。

r_u (u,v) ＝	∂r	＝	∂x	，	∂y	，	∂z	＝(x_u，y_u，z_u)　[ u 曲線に接する接線ベクトル ]

	∂u		∂u		∂u		∂u

r_v (u,v) ＝	∂r	＝	∂x	，	∂y	，	∂z	＝(x_v，y_v，z_v)　[ v 曲線に接する接線ベクトル ]

	∂v		∂v		∂v		∂v

	4-2　曲面のベクトル方程式と面積
f-denshi.com ［目次へ］　最終更新日：03/05/12
サイト検索

∂z	：	∂z	： -1＝J(yz/uv)：J(zx/uv)：J(xy/uv)
∂x		∂y

＝			F(u,v)		^1/2	｜J(xy/uv)｜dudv

＝			J(xy/uv)² ＋J(yz/uv)²＋J(zx/uv)²		^1/2	dudv

n ＝	r_u×r_v



	｜r_u×r_v｜

1．曲面のベクトル方程式