| 5 直交曲線座標 | |
| f-denshi.com [目次へ] 最終更新日:08/06/17 | |
| サイト検索 | |
普通,物理学の基本法則は直交直線座標系で示されます。しかし,実際の問題を解く場合,系が持つ対称性を利用して座標系を設定しなおすことがしばしば有効です。例えば,原子核とそのまわりを回る電子を扱うような問題では極座標(球座標)を用いて考察することが決定的に重要です。よく使われる座標系は他に円柱(円筒)座標,放物線座標などがあり,これらは直交曲線座標と総称される座標系の具体的な例となっています。これら直交曲線座標の一般論を知っておけば,公式集にまとめられている変換式,パラーメーターなどから機械的に各座標系で成り立つ関係式を導くことができます。関連ページとして,「実解析入門」15.積分変数の変換[#]を挙げておきます。
ここで,直交曲線座標の一般論を3次ベクトル空間で説明します(次元の拡張はほとんどの場合,容易です。) が,適時,具体例を参照してください。
[1] デカルトの直交座標系Σ={ex,ey,ez}の点(x,y,z)から,座標系Σ'={eu,ev,ew}で表した点[u, v, w]への座標変換を定める式が,
x=x(u, v, w), y=y(u, v, w), z=z(u, v, w) |
で与えられ,この変換のヤコビの行列式が 0 でない[#],すなわち,上の式は一意的に逆に解くこともでき,それを
u=u(x, y, z), v=v(x, y, z), w=w(x, y, z)
とします。[具体例確認→] ここで,基底ベクトル{eu,ev,ew}は空間の点によって変わり得る,つまり,点(=位置)[u, v, w]の関数(あるいは(x, y, z)の関数)であるとします。そして,eu,ev,ew が互いに直交しているとき,座標系Σ'を直交曲線座標(系)といいます。
[2] さて,一点を示す位置ベクトルを次のように書いておきます。
r = (x, y, z) = (x(u, v, w),y(u, v, w),z(u, v, w))
このとき,次のような用語を定義します。
[3] 座標曲線とは,
|
u曲線:v,w=一定の曲線で, |
をいいます[具体例確認→]。(それぞれ無数に存在する曲線群です。)
[4] 座標曲面とは,
u曲面:u=一定で与えられる曲面で,u(x, y, z)=u0
v曲面:v=一定で与えられる曲面で,v(x, y, z)=v0
w曲面:w=一定で与えられる曲面で,w(x, y, z)=w0
をいいます[具体例確認→]。
[5] 曲線座標の基底には,
(1)Σ':Pを通る3つの座標曲線に接する3つのベクトル
(2)Σ'':Pを通る3つの座標曲面に垂直な3つのベクトル → 3.相反直交曲線座標を参照 [#]
の(合理的な)2通り定義の仕方があります。
ここでは,(1)による導入を考えます。すなわち,接ベクトルと呼ばれる u-,v-,w- 曲線の各接線ベクトル[#] )を規格化(大きさを1とする)した3つのベクトルを座標系,Σ'の基底{eu,ev,ew}とするのです。それは,
u 曲線の接線ベクトル eu:
|
||||||||||||||||||||
とおくことができます。ここで,hu,hv,hwは規格化定数で,次の各ベクトルの大きさ,
hu= ∂r ,hv= ∂r ,hw= ∂r ∂u ∂v ∂w
で与えられ,計量係数(尺度係数)といいます[具体例確認→]。
一方,r の u,v,w に関する偏微分は,座標系Σでは,
|
・・・・・ [*] |
と記述ができます。[*]と[*]が相等しいとおけば,
|
⇒ 逆に解くと, [#] |
|
[**] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
を得ます[具体例確認→]。ある正規直交系から別の正規直交系への基底変換行列[#]はユニタリ(直交)行列[#]でした。もちろん,eu,ev,ew が互いに直交しているという条件の下でコツコツ計算しても得られる。
この[**]を用いると,座標系Σで(A1,A2,A3)とあらわされるベクトルを座標系Σ’へ変化するためには,
(A1,A2,A3)≡ A1ex+A2ey+A3ez
| = | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | eu+ | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | ev+ | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | ew | ||||||
| hu∂u | hu∂u | hu∂u | hv∂v | hv∂v | hv∂v | hw∂w | hw∂w | hw∂w |
| ≡ | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | , | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | , | A1 | ∂x | +A2 | ∂y | +A3 | ∂z | ||
| hu∂u | hu∂u | hu∂u | hv∂v | hv∂v | hv∂v | hw∂w | hw∂w | hw∂w |
とすればよいことがわかります。[具体例確認→]
[5−1] このとき,位置ベクトルの微分量について,
dr = (dx,dy,dz) = dxex+dyey+dzez
| = | ∂x | du+ | ∂x | dv+ | ∂x | dw | ex+ | ∂y | du+ | ∂y | dv+ | ∂y | dw | ey+ | ∂z | du+ | ∂z | dv+ | ∂z | ez | ||||||
| ∂u | ∂v | ∂w | ∂u | ∂v | ∂w | ∂u | ∂v | ∂w |
| = | ∂x | ex+ | ∂y | ey+ | ∂z | ez | du+ | ∂x | ex+ | ∂y | ey+ | ∂z | ez | dv+ | ∂x | ex+ | ∂y | ey+ | ∂z | ez | dw | ||||||
| ∂u | ∂u | ∂u | ∂v | ∂v | ∂v | ∂w | ∂w | ∂w |
=hueu du+hvev dv+hwew dw
≡[ hudu,hvdv,hwdw ]
つまり,線要素については, (dx,dy,dz) ⇔ [ hudu,hvdv,hwdw ]という対応があります。
[6] 次にいくつか重要な公式を導いておきましょう。 [**]式の両辺に,∂/∂x,∂/∂y,∂/∂zを上式から順にかけると,
| ∂ | ex= | ∂x | ・ | ∂ | eu + | ∂x | ・ | ∂ | ev + | ∂x | ・ | ∂ | ew |
| ∂x | hu∂u | ∂x | hv∂v | ∂x | hw∂w | ∂x |
| ∂ | ey= | ∂y | ・ | ∂ | eu + | ∂y | ・ | ∂ | ev + | ∂y | ・ | ∂ | ew |
| ∂y | hu∂u | ∂y | hv∂v | ∂y | hw∂w | ∂y |
| ∂ | ez= | ∂z | ・ | ∂ | eu + | ∂z | ・ | ∂ | ev + | ∂z | ・ | ∂ | ew |
| ∂z | hu∂u | ∂z | hv∂v | ∂z | hw∂w | ∂z |
これらを辺々足せば,
∇= ∂ ,
∂ ,
∂ ∂x ∂y ∂z
= ∂ ex+ ∂ ey+ ∂ ez = 1 ∂x ・ ∂ + ∂y ・ ∂ + ∂z ・ ∂ eu ∂x ∂y ∂z hu ∂u ∂x ∂u ∂y ∂u ∂z
+ 1 ∂x ・ ∂ + ∂y ・ ∂ + ∂z ・ ∂ ev hv ∂v ∂x ∂v ∂y ∂v ∂z
+ 1 ∂x ・ ∂ + ∂y ・ ∂ + ∂z ・ ∂ ew hw ∂w ∂x ∂w ∂y ∂w ∂z
= 1 ・ ∂ eu+ 1 ・ ∂ ev+ 1 ・ ∂ ew hu ∂u hv ∂v hw ∂w
= ∂ ,
∂ ,
∂ =∇ hu∂u hv∂v hw∂w
∇= ∂ ,
∂ ,
∂ ⇔ ∇= ∂ ,
∂ ,
∂ ・・・・・[***] ∂x ∂y ∂z hu∂u hv∂v hw∂w
が導かれました。さらに,
∇u = ∂u ,
∂u ,
∂u = 1 , 0 , 0 = eu hu∂u hv∂v hw∂w hu hu
∇v ,∇w も同様に考えて,
∇u = eu ,∇v = ev ,∇w = ew hu hv hw ・・・・・ [*]
なる関係が得られます。
他にも, eu ・eu = 1, ev ・ev = 1, ew ・ew = 1 を微分して,
∂eu eu = 0 : ∂u
∂eu eu = 0 : ∂v
∂eu eu = 0 : ∂w
∂ev ev = 0 : ∂u
∂ev ev = 0 : ∂v
∂ev ev = 0 : ∂w
∂ew ew = 0 ∂u
∂ew ew = 0 ∂v
∂ew ew = 0 ∂w
eu ・ev = 0, ev ・ew = 0, ew ・eu = 0 を微分して,
∂eu ev+eu ∂ev = 0: ∂u ∂u
∂eu ev+eu ∂ev = 0: ∂v ∂v
∂eu ev+eu ∂ev = 0: ∂w ∂w
∂ev ew+ev ∂ew = 0: ∂u ∂u
∂ev ew+ev ∂ew = 0: ∂v ∂v
∂ev ew+ev ∂ew = 0: ∂w ∂w
∂ew eu+ew ∂eu = 0 ∂u ∂u
∂ew eu+ew ∂eu = 0 ∂v ∂v
∂ew eu+ew ∂eu = 0 ∂w ∂w
|
は繰り返し用いることになります。 証明はこちら ⇒ [#]
[7] 体積要素 dVとして, (dx,dy,dz) ⇔ [ hudu,hvdv,hwdw ] より,
dxdydz = huhvhwdudvdw [具体例→]
各座標系で,ψ(x,y,z)=ψ(u,v,w) のとき,
gradψ = ∂ψ , ∂ψ , ∂ψ ∂x ∂y ∂z
⇒ gradψ= ∇ψ= ∂ψ eu + ∂ψ ev + ∂ψ ew hu∂u hv∂v hw∂w
= ∂ψ ∇u + ∂ψ ∇v + ∂ψ ∇w ∂u ∂v ∂w
[証明]は[***],[*] を見よ。
各座標系で,A = (Ax,Ay,Az) ⇔ [Au,Av,Aw] のとき,
divA = ∇A = ∂Ax + ∂Ay + ∂Az ∂x ∂y ∂z
⇒ divA = ∇A = 1 ∂(hvhwAu) + ∂(hwhuAv) + ∂(huhvAw) huhvhw ∂u ∂v ∂w
[証明]はこちら ⇒ [#]
rotA= ∂Az − ∂Ay , ∂Ax − ∂Az , ∂Ay − ∂Ax ∂y ∂z ∂z ∂x ∂x ∂y
⇒ rotA= ∂(hwAw) − ∂(hvAv) eu+ ∂(huAu) − ∂(hwAw) ev+ ∂(hvAv) − ∂(huAu) ew hvhw∂v hvhw∂w hwhu∂w hwhu∂u huhv∂u huhv∂v
= ∂(hwAw) − ∂(hvAv) , ∂(huAu) − ∂(hwAw) , ∂(hvAv) − ∂(huAu) hvhw∂v hvhw∂w hwhu∂w hwhu∂u huhv∂u huhv∂v
[証明]はこちら ⇒ [#]
div・gradψ= ∂2ψ + ∂2ψ + ∂2ψ ∂x2 ∂y2 ∂z2
⇒ div・gradψ= 1 ∂ hvhw ・ ∂ψ + ∂ hwhu ・ ∂ψ + ∂ huhv ・ ∂ψ huhvhw ∂u hu ∂u ∂v hv ∂v ∂w hw ∂w
[証明] ひたすら計算するのみ。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] 1.で述べた[#]ように直交曲線座標のもう一つ導入法として,「 (2) 点P を通る座標曲面に垂直な3つのベクトル 」を利用できます。すなわち,
u 曲面: u(x,y,z) = u0 に垂直な単位ベクトル →eu = ∇u(x,y,z)/Hu
v 曲面: v(x,y,z) = v0 に垂直な単位ベクトル →ev = ∇v(x,y,z)/Hv
w 曲面: w(x,y,z)= w0 に垂直な単位ベクトル →ew = ∇w(x,y,z)/Hw
で与えられます[#]。(↑添字が上にあることに注意せよ)ここで,Hu,Hv,Hw は規格化定数で,
Hu =|∇u|= { (ux)2+(uy)2+(uz)2 }1/2
Hv =|∇v|= { (vx)2+(vy)2+(vz)2 }1/2
Hw =|∇w|= { (wx)2+(wy)2+(wz)2 }1/2
です。eu,ev,ew が互いに直交している場合は,1.と同様な議論の繰り返しになるのでここでは省略して,より一般的な基底とその相反基底の関係する性質について触れておきます。
[2] 規格化されていない基底 { Hueu,Hvev,Hwew }と基底 { hueu,hvev,hwew }を考えると,これらは互いに相反系の関係[#]にあることが次の計算からわかります。まず,定義から,
Hueu = ∂u ex+ ∂u ey+ ∂u ez ∂x ∂y ∂z
hueu = ∂x ex+ ∂y ey+ ∂z ez ∂u ∂u ∂u
hvev = ∂x ex+ ∂y ey+ ∂z ez ∂v ∂v ∂v
などに注意しましょう。これらの関係を用いて,次の内積を計算すると,
Hueu・hueu=uxxu+uyyu+uzzu = 1
となります。最後の等号(=1)は合成関数,
u = u(x(u,v,w),y(u,v,w),z(u,v,w)) ←はベクトルではなくて関数 u{・・} という意味です。
を両辺,u で微分して,1=uxxu+uyyu+uzzu であることを使っています。(合成関数の微分は→[#])
同様に,Hvev・hvev=Hwew・hwew = 1 も示せます。
[3] 今度は内積,
Hueu・hvev = uxxv+uyyv+uzzv
を計算したいのですが,これは u = u(x(u,v,w),y(u,v,w),z(u,v,w)) の両辺を v で微分すると,
0 = uxxv+uyyv+uzzv
であることを使えば,0 であることがわかります。他の成分にどおしについても同様に,
Hiei・hjej = 0, i ≠ j
であることがわかります。したがって,基底 { Hueu,Hvev,Hwew } の下で成分表示されたベクトル,(A1,A2,A3)と基底 { hueu,hvev,hwew } の下で成分表示されたベクトル,[B1,B2,B3] の内積は,A1B1+A2B2+A3B3と成分表示してよいことがわかります。
一般的には異なる座標系の間で,
[4] 特に,{ Hueu,Hvev,Hwew } が正規直交系ならば,2つの座標系について,{ Hueu,Hvev,Hwew }= { hueu,hvev,hwew } が成立します。
証明 ⇒ [#]
[1] 空間の点を表す座標成分をそれぞれの座標系で,
(x,y,z) 直交デカルト座標 (Cartesian coordinate)
[ r,θ,φ] 球座標
と表すことにする。
[2] 座標変換式 (球座標)
x = r sinθcosφ,
y = r sinθsinφ,
z = r cosθ
逆に解くと,
r = ( x2+y2+z2 )1/2, [地球の標高] ←地球の中心からの
θ= cos-1( z/(x2+y2+z2)1/2 ), [地球の緯度]
φ= tan-1( y/x ) [地球の経度]
ただし, 0≦r<∞, 0≦θ≦π, 0≦φ<2π であって,θはz軸の正方向と位置ベクトルrとのなす角度,
(厳密にはz軸上の点ではφが不定となるので除くべきか? 0<r<∞, 0<θ<π,
0≦φ<2π)
[3] 座標曲線(球座標)は,
| r (r) = ( r sinθ0 cosφ0,r sinθ0 sinφ0, r cosθ0 ) ⇒ r 曲線 r (θ) = ( r0 sinθcosφ0, r0 sinθsinφ0, r0 cosθ ) ⇒ θ 曲線 r (φ) = ( r0 sinθ0cosφ ,r0 sinθ0sinφ, r0 cosθ0 ) ⇒ φ曲線 |
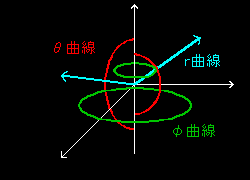
となります。
[4] また,座標曲面 (球座標)は,
r0 = ( x2+y2+z2 )1/2 ⇒ r 曲面
θ0 = cos-1{ z/(x2+y2+z2)1/2} ⇒ θ 曲面
φ0 = tan-1( y/x ) ⇒ φ曲面
[5] 計量係数 (球座標)
ベクトルの偏微分,
∂r =( sinθcosφ,sinθsinφ,cosθ) =hrer ∂r
∂r =( r cosθcosφ,r cosθsinφ,−r sinθ) =hθeθ ∂θ
∂r =(−r sinθsinφ,r sinθcosφ,0 ) =hφeφ ∂φ
より,
hr = 1, ← {( sinθcosφ )2+( sinθsinφ )2+cos2θ )}1/2
hθ= r ← {(r cosθcosφ)2+(r cosθsinφ)2+(−r sinθ)2}1/2
hφ= rsinθ ← {(−r sinθsinφ)2+(r sinθcosφ)2)}1/2
[6] 基底ベクトル(球座標)
基底変換の公式 (直交座標 ⇔ 球座標)
er = sinθcosφex + sinθsinφey + cosθez ex=sinθcosφer+cosθcosφeθ− sinφ eφ |
したがって,デカルト座標で,
( A1,A2,A3 )=A1ex+A2ey+A3ez ・・・ (1)
とあらわされるベクトル (ベクトル場) を球座標
[ Ar,Aθ,Aφ] =Arer+Aθeθ+Aφeφ
で表すと,(基底変換の公式ej を (1) に代入してej について整理すればよい。)
Ar = A1sinθcosφ+A2sinθsinφ+A3cosθ
Aθ= A1cosθcosφ+A2cosθsinφ−A3sinθ
Aφ=−A1sinφ +A2cosφ
となります。また,幾何学的配置は,
er ×eθ=eφ
eθ×eφ=er
eφ×er =eθ
となるように配置されます。
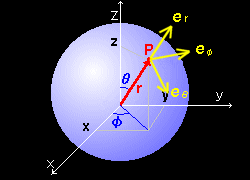
また,計量係数から,
体積要素[#]: dV=dxdydz=r2sinθdr dθdφ
線要素: dr=drer+rdθeθ+rsinθdφeφ
[7] 勾配(球座標) ∇ψ
gradψ = ∂ψ er + ∂ψ eθ+ ∂ψ eφ ∂r r∂θ rsinθ∂φ
[8] 発散(球座標) ∇A
divA = ∂(r2Ar) + ∂(sinθAθ) + ∂Aφ r2∂r rsinθ∂θ rsinθ∂φ
[9] 回転(球座標) ∇×A
rotA = ∂(sinθAφ) − ∂Aθ er + ∂Ar − ∂(rAφ) eθ + ∂(r Aθ) − ∂Ar eφ rsinθ∂θ rsinθ∂φ rsinθ∂φ r∂r r∂r r∂θ
[10] ラプラシアン(球座標) ∇2ψ
div・gradψ= 1 ∂ r2 ∂ψ + 1 ∂ sinθ ∂ψ + 1 ∂2ψ r2 ∂r ∂r r2sinθ ∂θ ∂θ r2sin2θ ∂φ2