Appendix １　３次元ベクトルの座標変換
f-denshi.com  最終更新日：07/10/07  (具体例を入れました。)
サイト検索

　　ベクトル空間 V を生成する基底が違えば，それに応じてV の元 x の(成分)座標も変化します。そこで異なる２つの基底(＝座標系)Σ とΣ'との関係が与えられたとき，ベクトル座標成分がどのような関係式で結ばれるべきか示しておきましょう。n次元の(反変，共変)ベクトル空間の場合は本文中であつかってます。ここではもっともよく使われる３次元ユークリッド空間を用いて具体的に説明しましょう。

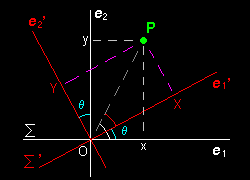［１］　特別な場合として，３次元空間の z 軸周りで角度θの回転を例として挙げておきます。その場合，２つの座標系Σ とΣ' の（正規直交）基底どおしの関係は右図から次のように与えられます。   

e'₁＝ cosθe₁＋sinθe₂
e'₂＝-sinθe₁＋cosθe₂
e'₃＝　　e₃

このとき，任意のベクトルは，

P ＝xe₁＋ye₂
　＝Xe'₁＋Ye'₂

の２とおりの表し方がありますが，xとX，および，yとYの値はθ＝0 の場合を除いて異なる値となるはずです。この関係は幾何学的な考察から，

	x		＝		cosθ	-sinθ	0			X
	y				sinθ	cosθ	0			Y
	z				0	0	1			Z

で表されることが分かります。　（右図をよーく見て考えてください。）

これを一般化された基底変換の下での成分どおしの関係，

 (x,y,z) [座標系Σ]　　⇔　　(X,Y,Z) [座標系Σ']

を導出することがここでの目的です。

［２］　今，２つの座標系の基底ベクトルを，

Σ ＝｛e₁，e₂，e₃｝
Σ'＝｛e'₁,e'₂,e'₃｝

とします。そのとき，ベクトルx はそれぞれの座標系で，

x＝ x₁e₁  ＋x₂e₂   ＋x₃e₃　   (座標系Σ  )　　　　　
x＝x'₁e'₁＋x'₂e'₂＋x'₃e'₃  　(座標系Σ ')　　　　　

と表されます。同じベクトルであっても，それを表すための基底（座標系が）が異なれば，座標成分も異なってくるのは当然です。これから，基底ΣとΣ'との関係（変換規則）が与えれたときのべクトル成分，

との関係式を求めます。

［３］　まず，ΣとΣ'との関係がどのように与えられるべきかは，Σ ' の基底ベクトルe'_j も一つのベクトルですから，座標系Σ の基底を用いて一次結合で表せるはずです。それを

すなわち，

e'1＝p11e1＋p21e2＋p31e3≡(p11,p21,p31) e'2＝p12e1＋p22e2＋p32e3≡(p12,p22,p32) e'3＝p13e1＋p23e2＋p33e3≡(p1n,p2n,p33)

と， p_jk によって基底間の関係を与えることとします。なお，これは形式的に，

e'1 　 p11 p21 p31 e1 e'2  ＝ p12 p22 p32 e2 e'3 　 p1n p2n p33 e3

⇔

e'1 ＝　tP e1 e'2 e2 e'3 e3

と書いてもいいでしょう。ここで，p_kjを成分とする行列を転置行列で，^tPと定義した理由は慣用であって，最終的に成分の変換則が「主役」になるようにPが定義されるからです。

(↑注意：　教科書によっては，e₁＝　p₁₁e'₁＋p₂₁e'₂＋p₃₁e'₃　などと逆に与える場合があります。)

［４］　次にベクトルx は２とおりの基底，どちらで表しても同じだということを示す等式，

x₁e₁＋x₂e₂＋x₃e₃ ＝ x'₁e'₁＋x'₂e'₂＋x'₃e'₃

の右辺に［３］で書き表した e'₁，e₂'，e₃' を代入してe₁，e₂，e₃　について整理すると，

x₁e₁＋x₂e₂＋x_ne₃　＝　(p₁₁x'₁＋p₁₂x'₂＋p₁₃x'₃)e₁
　　　　　　　　　　＋(p₂₁x'₁＋p₂₂x'₂＋p₂₃x_'3)e₂
　　　　　　　　　　＋(p₃₁x'₁＋p₃₂x'₂＋p₃₃x'₃)e₃

ここで，e₁，e₂，e₃　は１次独立なので上式の両辺の各e_ｊ　の係数が等しいとして，

x₁　＝ p₁₁x'₁ ＋p₁₂x'₂ ＋p₁₃x'₃
x₂　＝ p₂₁x'₁ ＋p₂₂x'₂ ＋p₂₃x'₃
x₃　＝ p₃₁x'₁ ＋p₃₂x'₂ ＋p₃₃x'₃

すなわち，それぞれの座標成分の間には，

の関係が得ます。この結果を行列を用いて表すと，

ここで，(↓以後色分けは省略。)

P ≡ p11 p12 p13  ＝(p1 p2 p3)　；　ただし， pj ≡ p1j p21 p22 p23 p2j p31 p32 p33 p3j

を　座標変換の行列　(または，基底変換の行列)　といいます。

［５］　また，

座標変換の行列 P は正則行列でなければならない。

ことが以下のようにわかります。Σ がV の基底であるならば，e'_j ＝ Σ p_kje_k　と表せるように各e_j も

e_j ＝ Σ q_kje'_k　

とあらわせるはずで，上と同様な議論から逆方向への座標変換の行列Q が得られ，

　x' ＝ Qx　

なる関係が導かれます。これを先程求めた関係，x ＝Px'　に代入すれば，

x  ＝ Px' ＝ P(Qx) ＝ (PQ)x

つまり，PQ＝E ［単位行列］　でなければならず，これは Q ＝ P^-1 であることを示しています。結局，

x'＝ P-1x

記号を整理すると，

［６］　最後に正規直交基底どおしの間での座標変換について述べておくと，

ベクトル空間の基底Σ，Σ'が正規直交系であれば，座標変換の行列Pは直交行列である。

ことが示せます。なぜなら，基底変換を e'_j＝Σ p_kje_k　とすると，　

　　　δ_jk ＝ (e'_j,e'_k )　　　←e'_j，e'_k　が正規直交基底なので
　　　　　　＝ (p_1je₁＋p_2je₂＋p_3je_n，　p_1ke₁＋p_2ke₂＋p_3ke_n)
　　　　　　　  ↓     e_j，e_k　が正規直交基底(e_j,e_k )＝δ_jk なので
　　　　　　＝ p_1jp_1k＋p_2jp_2k＋p_3jp_3k　　
　　　　　　＝ (p_j,p_k )　　

となり，P＝(p₁ p₂ p₃) が直交行列[#] であることがわかります。

また，直交行列Pの逆行列がPの転置行列^tPで与えられる[#]ことから，

	x'1				p11 p21 p31			x1		⇔　x ' ＝ tPx　　［正規直交基底の場合］
	x'2		＝		p12 p22 p32			x2
	x'3				p13 p23 p33			x3

［目次へ］