| 4-1 曲線のベクトル方程式と長さ | |
| f-denshi.com [目次へ] 最終更新日:03/05/12 | |
| サイト検索 | |
[1] 3次元ユークリッド空間の位置を示す位置ベクトルr をパラメーター t を用いて
r = r (t)=(x(t),y(t),z(t)) ; a≦t≦b
と表わすとき,このベクトルの(先端の)軌跡は3次元空間の曲線を表します[#]。これを曲線のベクトル方程式といいます。
(力学ではパラメーター t を時刻とみなし,r (t)は時刻 t における質点の位置と考えます。)
[2] このr (t) のt についての微分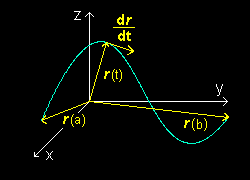
r '(t)= dr = dx , dy , dz dt dt dt dt
を接線ベクトルといいます。また,接線ベクトル,|r '(t0)|= 0 のとき,r (t0) を曲線の特異点といいます。そうでないときこの点を正則点といいます。曲線上のあらゆる点で連続微分可能かつ正則点である曲線をなめらかな曲線(正則な曲線)といいます。
(力学では軌跡の接線,r '(t)は時刻 t における質点の速度v を意味します。)
[3] 曲線の長さの微小量 ds=|dr (t)|は,
ds = dx2+dy2+dz2 =|r '(t)|dt
=
dx 2 + dy 2 + dz 2 dt dt dt dt [線素]
となります。
[4] 媒介変数として適当な定点(例えばr (a))からの曲線の弧長 s を選ぶ(つまり,上の式で t → s とする) と,
|r '(s)|= 1
となります。このような大きさ1の接線ベクトル,
t (s)≡r '(s)=
dr = dx , dy , dz ds ds ds ds
を接線単位ベクトルと呼びます。
[5] また,このt (s) をもう一回微分すると,
t '(s)=
dt = d2x , d2y , d2z ds ds2 ds2 ds2
となりますが,この大きさが1となるように規格化した,
n (s)≡ 1 t '(s) |t '(s)|
を主法線単位ベクトルと言います。(力学では加速度方向を示す単位ベクトルに相当します。)
法線'' と言う理由は,
| |r '(s)|2 = | dr | 2 | = | dx | 2 | + | dy | 2 | + | dz | 2 | = 1 | ||||||||
| ds | ds | ds | ds |
の両辺を s で微分して,
2 dx ・ d2x + 2 dy ・ d2y + 2 dz ・ d2z = 0 ds ds2 ds ds2 ds ds2
これは内積: t ・t '= 0 であること,つまり,t とは n (∝t ') とは互いに直交しているのです。
また,t (s) の s を新しく時間と見直せば,t (s)は速度方向,t '(s)は加速度方向を表し,
|t (s)|= 一定 ⇒ n (s)⊥t (s)
という関係は,
速度の大きさ一定 ⇒ 加速度と速度は直交している
という物理的な意味を読みとることができます。また,加速度の方向は力の働く方向と同じなので,結局,中心力を受けた等速円運動において成り立つ関係を述べたことになっています。
一方,n ∝t ' より,スカラーκ(s)を用いて,
t '(s) = κ(s)n (s)
と書くことができますが,κ(s)を曲率といいます。また,この逆数 1/κ を曲率半径といいます。半径と呼ぶ理由は,図形が半径R円の場合,
r (s) = ( x(s),y(s) ) = ( R・cos(s/R),R・sin(r/R) )
とおいて曲率を計算して見ると(演習),κ(s)=1/R となるからです。曲線が円を表していない場合は,そのカーブにもっともフィットする円の半径という解釈でよいでしょう。
[6] さらに,これら両方に垂直な従法線単位ベクトル が次のように定義されます。
b (s) =t ×n
以上の3つのベクトルの関係は下図のようになります。
|
[7] 曲線r (t); a≦t≦b の中で,始点と終点が等しい,つまりr (a)=r (b) のとき閉曲線といいます。
この場合,曲線の方向には,時計回り,反時計回り2通り(一方がパラメータt
の増加する方向ならば,他方は減少する方向)があります[#] が,
(1)曲線がこの画面内にある場合は反時計回りの方向を正にとります。 ←角度の正方向と同じ
(2)3次元空間内に置かれている曲線はその場で定義する必要があります。
(閉曲線の向きの定義は絶対的なものではなく,(物理の)問題ごとに定義されることも多いので注意が必要です。)
SUSTAINABLE TOKIWADAIGAK SINCE 2002