| 11 C1写像:ヤコビ行列と陰関数定理 | ||
| f-denshi.com [目次] 最終更新日:この章,いつか2つに分割します。 | ||
| サイト検索 | ||
[1] C1級の関数[#],x=x(u,v), y=y(u,v) を組み合わせた写像:
Φ :(u,v) → (x,y)=(x(u,v),y(u,v)) ; (x,y),(u,v)∈R2
を C1写像といいます。これは2つの実数の組(u,v)から2つの実数の組(x,y)を対応させる関数です。
Φ(u,v)=(x,y)
= (x(u,v),y(u,v))
と書くこともあります。
[2] 具体例として,
(1)線形写像 (u,v) → (x,y)
x = a b u y c d v
(2)直交−極座標変換 (r,θ) → (x,y)
x = r・cosθ
y = r・sinθ
などがあげられます。重要な例として他に,複素関数があります。実部,虚部の2実変数関数のように考えて,値域を制限することで,C1写像と呼んでいい場合があります。
[1] 領域U上で定義されたC1写像:Φ(u,v)=(x(u,v),y(u,v)) を考えます。
(u,v)=(a,b) における x=x(u,v),及び y=y(u,v) のテーラーの展開
[#]は,
Δx=xu(a,b)Δu + xv(a,b)Δv +ο(d)
Δy=yu(a,b)Δu + yv(a,b)Δv +ο(d)・・・・・・・[*]
ただし,
Δx=x(u,v)−x(a,b)
Δy=y(u,v)−y(a,b)
Δu=u−a
Δv=v−b
と書けます。ここで,xu(a,b)は関数: x(u,v) の点(a,b)における u に関する偏微分係数で,他の偏微分係数も同様に表しています。また,ο(d) は2次以上の高位の無限小です。
[2] ここで,Δu,Δv が小さく高位の無限小ο(d) を無視すれば,上の[*]式は行列を利用して
Δx = xu(a,b) xv(a,b) Δu Δy yu(a,b) yv(a,b) Δv
と表記することができます。この行列はたいへん重要で,
xu(a,b) xv(a,b) yu(a,b) yv(a,b) =
∂x ∂u u=a,v=b
∂x ∂v u=a,v=b
∂y ∂u u=a,v=b
∂y ∂v u=a,v=b
をヤコビ行列といい,J(Φ)a,b と書くことにします。
[3] また,この行列の行列式についても次のように名前と記号を定義しておきます。
|
ヤコビ行列の行列式
を点 (a,b) におけるヤコビの行列式,または,ヤコビアンと呼ぶ。また,領域 U上の任意の点(u,v)について考えるときは,
または,
と書く。 |
このヤコビの行列式は,後ほど重積分の変数変換の公式[#]などにも使います。
[1] ヤコビ行列を利用して導かれる重要な定理を述べます。
| 逆写像定理 R2 から R2への写像 Φ(u,v): (u,v) → (x,y)=(x(u,v),y(u,v)) において, (A) Φ(u0,v0) = (x0,y0) (B) Φは C1写像 (C) J(Φ)u0,v0が正則行列 であるならば, 点(u0,v0) を含む十分小さな領域: U ,点(x0,y0)を含む十分小さな領域: X を適当に定めれば, Φ は U から X への1対1写像となる。 |
厳密な証明⇒ [#] は長いので省略し,考え方を簡単に示します。
証明で重要な役割を演じるのはヤコビ行列で,
Δx = xu(u0,v0)) xv(u0,v0) Δu Δy yu(u0,v0) yv(u0,v0) Δv
をみると,(A),(B)から(u0,v0) の近傍は (x0,y0) の近傍に写ることがわかります。←Φの連続性が効いてます。
そして,(C):ヤコビの行列に逆行列が存在するので,上式に逆行列をかければ,逆写像:(Δx,Δy)→(Δu,Δv)を示す行列の関係式がえられ,Δx,Δy
が 0 に近づく極限では(u0,v0)と(x0,y0)の近傍は1対1で対応してしまうだろうということです。
[2] 次はこの定理の重要なバリエーションです。
| 陰関数定理 ある領域において陰関数:F(x,y)=0 とその偏導関数:Fx(x,y),Fy(x,y) が連続であるとする。領域内の一点(x0,y0) にて, (A) F(x0,y0) = 0ならば,y = f(x) が x の関数 として一意的に定まる。このとき, (1)' y = f(x) は連続関数 である。 |
この定理の意味するところを具体的に説明しましょう。
例えば,円の方程式:x2+y2 = 25 を考えます。このとき,陰関数定理の記号に合わせると,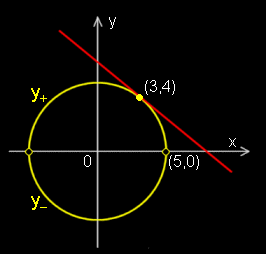
F(x,y) = x2+y2−25 ; |x|,|y|≦5 ←考えてる領域
Fy(x,y) = 2y
Fx(x,y) = 2x
となります。そこで,領域内の x0=3,y0=4 の点を考えると,
F(3,4) = 0 ←(A)
Fy(3,4) = 8 ≠ 0, ←(B) Fx(3,4) = 6
なので条件(A),(B)を満足しています。したがって,
y+ = f(x) = (25-x2)1/2 ←(1)'連続関数,かつ(2)'
が x の関数として一つ定まり,この点の微分係数,
dy = − Fx(3,4) = − 3 ←(3)' dx Fy(3,4) 4
すなわち,この点(3,4)における円の接線の傾きが求められる。というのが定理の意味です。
[3] 定理が使えないような場合も見てみましょう。例えば,同じ関数で,x0=5,y0=0では,
F(5,0) = 0
Fy(5,0) = 0 ← (B)をみたしていない
なので,(B) が成り立っていません。この場合,x の陰関数は一意的ではありません。実際,点(5,0)は
y+ = (25-x2)1/2
y- =−(25-x2)1/2
の2つの関数どちらでも表せます。
[4] この定理の有用性は,例えば,
F(x,y) = y5−xy+1 =0
は y についての5次方程式となっていますが,これを四則演算と根号で, y=f(x)
と解くことはできません。(難しいというのではなく原理的に不可能:アーベル・ガロア)
しかし,上の定理を用いて導関数: dy/dx は求めることができるのです!(このF(x,y) の偏微分はチョー簡単。[答] y/(5y4-x))
[5] 最後に熱力学など応用面でよく使う関係式[#] を紹介しておきます。全微分可能な陰関数: F(x,y,z)=0 について,
∂x z ・ ∂y x ・ ∂z y = −1 ・・・・(**) ∂y ∂z ∂x
が成り立ちます。ここで,(∂x/∂y)z は,「陰関数 F(x,y,z)=0 を xについて解いた関数 x(y,z) を,zを定数とみなし,y で偏微分する」という意味です。
証明は,全微分,
dF = ∂F dx + ∂F dy + ∂F dz = 0 ∂x ∂y ∂x
において,z=一定 ⇒ dz=0 とすれば,
∂F dx + ∂F dy =0 ∂x ∂y ⇔
∂x ∂y z = −
∂F ∂y
∂F ∂x
さらに同様な式を x=一定, y=一定 として求めて,得られた3つの式を辺々かけあわせれば,
|
・ |
|
・ |
|
= | − |
|
− |
|
− |
|
=−1 | ||||||||||||||||||||||||||||||||||||
|
|
|
となります。