| 1 電磁気学の体系と単位について | ||
| f-denshi.com [ 目次へ ] 最終更新日:10/08/08 体系化を示す図を書き直しました | ||
| サイト検索 | ||
1.はじめに
[1] 電気と磁気,ともに古くから知られている物理現象ですが,はじめはまったく別々の現象であると考えられていました。しかし1820年,電流が磁石に力を及ぼすことをエルステッドが発見し,両者は互いに密接な関係にあることがわかりました。その後,この現象はアンペアの法則(モーターの原理),ファラデーの法則(発電の原理)として確立され,電磁気学と呼ばれる一つの理論体系にまとめられました。電磁気学の基礎はこの時代に見出された実験事実を基礎にしていますが,現在,この体系に必要な原理は,古典力学に加えて,(←教えてくれた方ありがとう。17/5/25)
電磁気学の原理:
(1) クーロンの法則 (重ね合わせの原理) |
となっています。つまり,実験事実として証明抜きで受け入れるべき法則はこの3つだけであり,これらの法則から,ファラデーの法則,アンペールの法則,電磁波の発生など(19世紀の現象論的)電磁気現象をすべて説明することができます。この講義は効率良く電磁気学を復習するという観点からこの3つの原理から演繹的に電磁気学の基本体系を次のように示しました。歴史的な経緯は完全無視!
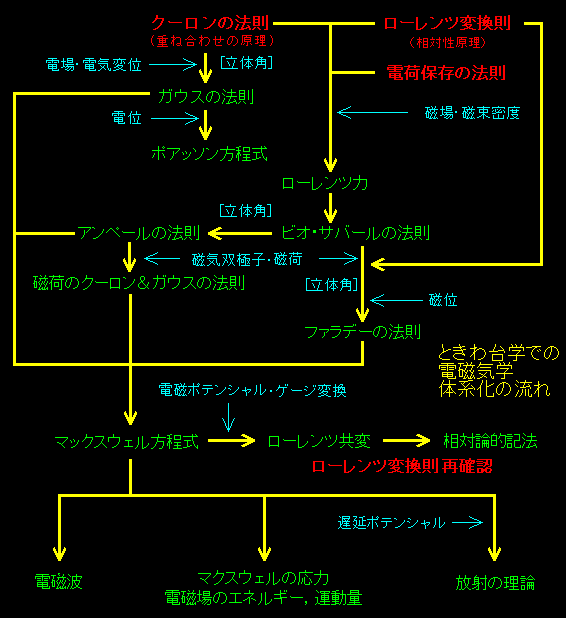
緑色で示している著名な法則は公理として与えられているのではなく,3つの基本原理から導出可能だという点に注意してください。
水色の部分は便宜的な変数の導入やベクトル解析の公式利用です。
なお,(A)光速度がすべての慣性系から同じであること(光速度不変の原理)も,(B)マクスウェルの方程式がすべての慣性系で同じ形となること(特殊相対性原理)も,相互の慣性系の時空の変数,x,y,z,t に対してローレンツ変換則(ローレンツ対称性)を要求するので,お互い交換可能な等価な原理と考えられます。しかし,人間の感性に照らし合わせて多くの物理的内容を含むマクスウェルの方程式 (まあ,1行で書くこともできますが,) を原理として出発点におくことには違和感があるので,このサイトでは(A)を原理として採用しました。
そのような構成の中では,光速度不変の原理から導かれたマクスウェルの方程式がローレンツ共変であることは当たり前であり,そのような意味で上図で「ローレンツ変換則再確認」としています。
以上,もっと簡明な言い方をすれば,
電磁気学固有の原理は,クーロンの法則で尽きていて,それをアインシュタインの特殊相対性原理(←これはすべての物理現象に適用できる時間空間の根本原理)と矛盾しないように,(電荷が静止して見える慣性系だけでなく ) 任意の慣性系にまで拡張してゆけば,電磁気学の諸法則・体系 は一意的に定まる。
ということをこのホームページでは示しています。(もちろん,体系の中に数学的な自由度 (例えばポテンシャルの基準点の選び方など)すらまったくないというようなことを言ってるわけではありません。)
[2] 電磁気学では現在,様々な単位系が使用されており,論文は読むときはもちろん,教科書を読むときにもどのような単位系が使われているのか注意を払う必要があります。このホームページでは現在,標準的と考えられるMKSA有理単位系,EH対応を用いています。EH対応のもとでは電場と磁場,つまり電荷と磁荷が数学的な対称性を示すように電磁気学の体系化が行われており,各物理量に使われる単位にも優れた対称性が見られます。ただし,このHPでの電磁気学の体系化方法はEH対応とEB対応とでどちらが優れているかという議論に与するものではありません。
[1] まず,電磁気学に使われる主要な物理量の記号と単位について,電荷と磁荷の対称性に注目しながら一覧表にしてみました。電磁気学の学習の際,必要に応じて参照して下さい。本格的な解説は広島大学の山崎先生のmonograph「電磁気学における単位系」(PDF)が読みやすいと思います(ネット上で簡単に検索にかかります。版を重ねて益々充実しています)ここでは,
| 電気 | 磁気 | |||
| 単位 | 物理量と記号 | 物理量と記号 | 単位 (EH対応) | 単位 (EB対応) |
| C [A s] | 電荷 Q,Qe | 磁荷 Qm | Wb [ Vs ],[JA-1] | - |
| C | 電束 Ψe | 磁束 Ψm [Φ] | Wb [ NmA-1 ] | - |
| V [J/C] | 電位 φe [ψ] | 磁位 φm | A | - |
| V | 電圧 V | 電流 I | A | - |
| V・m-1 [N/C],[kgm/(Cs2) | 電場 E | 磁場 H | A m-1 [N/Wb] | - |
| C・m-2 | 電束密度 D | 磁束密度 B | Wb m-2 [T] | - |
| Cm-2 | 分極P | 磁化M [Pm] | Wb m-2 | Am-1 |
| C・m | 電気モーメント p | 磁気モーメント m | Wb m | Am2 |
| Fm-1 [C/(Vm)] | 誘電率 ε | 透磁率 μ | Hm-1 [Wb/Am] | - |
| Fm-1 | 電気感受率 χ,χe | 磁気感受率 χm | Hm-1 [Wb/Am] | - |
| 無次元 | 比電気感受率 χr | 磁化率 χm | - | 無次元 |
| F [C/V] | 静電容量 C | インダクタンス L | H [ Wb/A] | - |
| m | 長さ r, L | 水色の[ ]は単位の別表現を併記したものです。 磁気感受率χmを磁化率と呼ぶこともあります。 E-H対応での磁化Mを磁気分極Pmと呼ぶことがあります。 つまり,EH対応,E-B対応にかかわらず, 磁化率の定義には2通りあるので注意が必要。 |
||
| N [kg・m/s2] | 力 F | |||
| J [N・m] | 仕事 | |||
| D = ε0 E + P | B = μ0H + M | B = μ0 ( H + M ) | ||
| ε =(ε0+χe)=ε0 (1+χr) | μ= (μ0+χm) | μ=μ0(1+χm) | ||
| Q = CV (Φe=CV) | =L・I | - | ||
| H = εv × E | E = μv × H | - | ||
[C] クーロン (coulomb)
[A] アンペア(ampere)
[V] ボルト (volt)
[Ω] オーム(ohm)
[F] ファラッド(farad)
[H] ヘンリー (henry)
[Wb] ウェーバー(weber)
[m] メートル(meter)
[J] ジュール(joule) =1[Ws]ワット秒
[N] ニュ−トン(newton) =[kg・m/s2]
[T] テスラ(tesla) =104[G]ガウス(gauss)
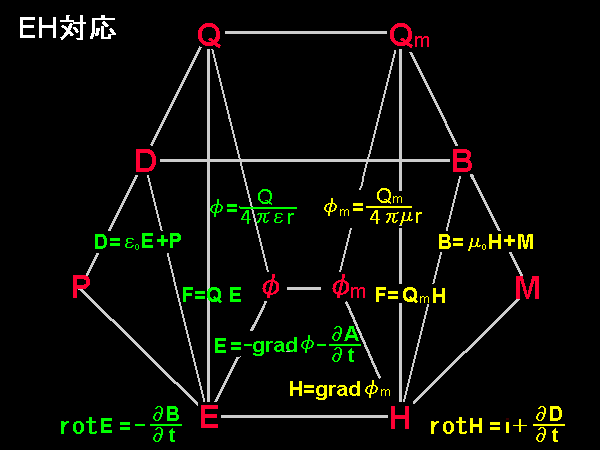
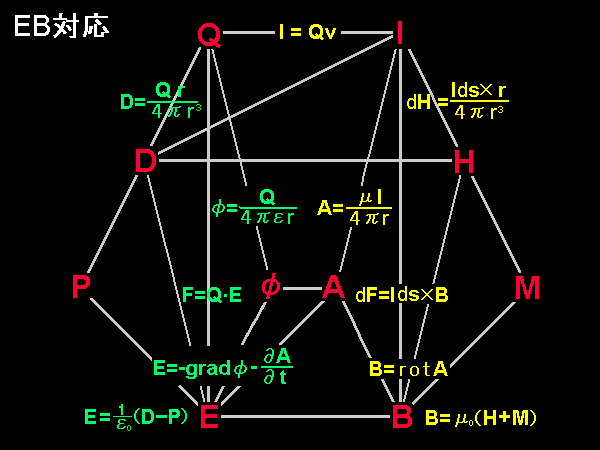
[1] 電磁気学に内在する様々な対称性に気づくことは,それ自身美しいだけでなく,電磁気学を理解・習得する助けにもなります。本テキストではEH対応と呼ばれる対称性に重点をおいて説明,電磁気学の構成をおこなっていますが,EB対応との比較や違いを理解しておくことも実用上欠かせません。そこで両方の場合についてどのような物理量や方程式が対称的な関係にあるのか図にまとめました。電磁気学で行き詰まったときには,電磁気学全体を見渡すこの図の中に何かヒントが見つかるかもしれません。
 |
 |
E-H対応が優れているところは,電気の体系と磁気の体系との数学的な対応(←見た目)が美しいことで,これは物性論などで重要な電気モーメント,磁気モーメントの単位を比べてみる[#]だけでもよくわかります。これ以上説明は必要ないでしょう。
一方,E-B対応が優れているところは,物理的な事実を重視して体系が組み立てられることです。電磁気学で本質的な物理量は電荷Qと電流I,または電場Eと磁気誘導Bです。電気変位Dはいわば,物質集団を近似的に取り扱うために便宜的に導入されたパラメータであり,磁場も,磁気現象を電気現象になぞらえて理解するために導入された便宜的な物理量。
ただし,当サイトでは,アイシュタイ相対性原理の下でクーロンの法則を簡明に記述するための方便として,E とH,B を定義しているので,E-H対応とE-B対応のどちらにも与するものでないことは理解していただけると思います。
Q,q:電荷
I,j:電流,電流密度
D:電気変位 [ 電束密度 ]
H:磁場
P:電気分極
V:電位
A:磁気ポテンシャル
M:磁化
E:電場
B:磁束密度