３　ガウスの法則
f-denshi.com  [目次へ ］最終更新日：　　22/02/05
サイト検索

１．ガウスの法則

　［１］　クーロンの法則からガウスの法則と呼ばれる次の法則が導かれます。

法則と呼ばれますが，クーロンの法則から必然的に導かれます。

［２］　まず，電場に関する面積分の物理的な意味（考え方）を考えてみましょう。

下図は点電荷 Q ＞0　から電気力線　(＝正電荷ならば，電気力線はそこから湧き出している水の流れに例えることができます。この水を多く受ければ受けるほど正電荷は大きな力を受けるというイメージ。)　が無限遠に向かってのびている様子を平面的に模したものです。

閉曲線C1，C2は電荷を内部に含む閉曲面のつもり，C3は電荷を内部に含まない閉曲面の例のつもりです。電気力線の定義では電荷Qから出ていくその本数はQ/εで途切れることはありません。また，電気力線の (その垂直方向の) 面密度は電場E の大きさに比例することを思い出して下さい[#]。

すると，ガウスの法則の左辺＝面積分の中身，E ・dS　の意味 [#] はその微小面積 dS を通り抜ける電気力線の本数を表すので，その閉曲面全体にわたるその積分とは閉曲面を内から外に向かって (正方向に) 出ていく正味の電気力線の本数を表しているのです。

したがって，その正味の本数を数えると，

C1，C2の場合　⇒　Q/ε 本　（Qから発するすべての電気力線）
C3の場合　　　　⇒　　０　 本   （進入本数＝出てゆく本数）

であることは上図を見ればすぐに理解できます。以上がガウスの法則の意味するところです。

（右図は２次元的に描いてますが，３次元の様子を思い浮かべることはそう難しくはないですね。）

［３］　以上の内容を厳密に表したのがガウスの法則です。

証明　　　立体角 ⇒ [#] の知識を前提としています。

　電荷には重ね合わせの原理 [#] が成り立つので，点電荷について示せば十分です。

　原点にある電荷Q の作る電場は［#］，

E  ＝ kQ・	r
	|r | 3

と電荷からの距離 r の関数で表されました。この両辺を平曲面S上で面積分を行うと，

	E ・dS　＝ kQ			r　･dS
				|r | 3

と表記されます。

ところが，右辺は点電荷から見た閉曲面の立体角の微分 dΩ の定義[#]，　

dΩ　≡	r　･dS	＝		r	･	n0	dS
	r3			r			r2

そのものです。これを用いれば，

E ・dS　＝ kQ　 dΩ  ＝ （ Q/4πε） dΩ

となります。　　　　（ k ＝ 1/4πε ）

［４］　ここで立体角の積分値は次の２通りが考えられます[#]。

A．電荷が閉曲面の内部の点 O にあるとき，

dΩ＝4π　　(単位球面の面積)

B．電荷が閉曲面の外部の点 O’にあるとき

dΩ＝0

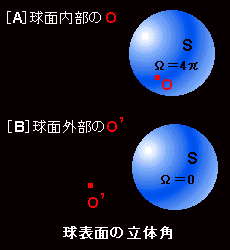
この２つケース[#]をまとめて表現するとガウスの法則となります。

［５］　ガウスの法則の他の表現をまとめておきます。まず，微分形のガウスの法則と呼ばれるものです。アボガドロ数程度の原子が集まってできる物質の電磁気現象の記述では，電荷を点電荷の集まりとしてではなく，空間内に連続的に分布しているとみなす方が便利です。

そのような場合，電荷分布は電荷密度ρ（r ）を用いて表わすことができます。電荷密度を用いると，閉曲面S の内部 V の全電荷量 Q は

Q　＝

ρ（r） dV

でえられます。一方，ベクトル解析のガウスの定理[#]によると，

	E ・ dS　　⇒			div E  dV

と書き換えられます。　よって，ガウスの法則 [*] 式は，

	divE dV　＝	4πk		ρ（r）dV

これが任意の領域 V について成り立つならば，積分内部を比較して，

ガウスの法則の微分形 　　　divE 　＝ 4πkρ（r ）　＝ρ（r ） / ε

が得られます。

［６］　その他，ガウスの法則のいろいろな表現を列挙しておきます。　

詳しい説明は後ほど順に行っていきますので，今は眺めるだけで結構です。

２．対称性のある静電場

　ガウスの法則は対称性のある電場を具体的に求めるときに大きな威力を発揮します。例としてよく用いられる電場をいくつか計算して見ましょう。

［１］　半径R の球の表面に一様に分布している電荷 (全電荷＝Q [C] ) のつくる電場

電場も球対称性を持っているはずですから半径 ｒ ＞ R  の球面を考えたとき，その球面上のどこでも電場の大きさは等しく，中心から r　方向を向いています。したがって，ガウスの法則より，

r ＞ R のとき，電場の大きさは，

E・dS　＝ E ･ 4πr2 ＝ Q / ε0

∴　E　＝ Q / 4πε₀r²

r ＜ R　のとき，電場の大きさは，

E ＝ 0

［２］　無限にのびる直線に一様に分布している電荷（線電荷密度σ’[C/m] ) の作る電場

　電場は直線のまわりに回転対称性を持っているはずですから，その中心に直線が通る半径 R の高さ L の円筒形を考え，この表面上についてガウスの法則を適用します。円筒形の上面と底面では対称性から電場の面に対する垂直成分は0です。側面では電場の大きさはどこも同じで，方向は直線から放射状，言い換えると側面に垂直で外を向いています。したがって，

E ・ dS　＝ E ･ 2πRL ＝(σ’L)/ε0

∴　　E ＝	σ’	［直線から垂直距離Rの点で］
	2πε0R

もし，ガウスの法則を用いないのであれば，次のように積分を行うことになります。

dE ＝sinθ	σ’dz	，sinθ ＝ R / r，　r ＝（ R2+z2）1/2
	4πε0r2

∴　 E ＝			σ’sinθ	dz ＝	σ’
			4πε0r2		2πε0R

［3］　無限に広がる板面に一様分布する電荷（面電荷密度σ[C/m²]　）の作る電場

　電場は平板を境に上下の対称性を持っているはずですから，面対称になるような高さr の円筒を考え，この表面上についてガウスの法則を適用します

E・dS　＝2E･S (円筒の上下)＋0 (円筒の側面) ＝ σS / ε0

∴　　E ＝	σ	[方向は面と垂直外向き]
	2ε0

［４］　半径R の球の内部に一様に分布している電荷 (電荷密度ρ [C/m³] ) がつくる電場

ｒ＞R のときは，［１］の場合と同じで　E＝Q/4πε₀r² である。ただし，4πR³ρ/3＝Q　であり，

E＝R³ρ/3ε₀r²

r＜Rのときは，半径 r の球の内部の電荷は［4πr³ρ/3 ］であるから，ガウスの法則より，

E・dS　＝ E ･ 4πr2 ＝ ［4πr3ρ/3 ］/ ε0

E ＝ rρ/ 3ε₀

となります。

［目次へ］