| 3 行列の階数と核 | ||
| f-denshi.com 最終更新日:07/10/02 | ||
「はじめての線形代数」PDF版がこちらからダウンロードできます。
⇒ 無料見本
[1] 前章に続き,次のように表される連立方程式(1)とその付随する同次方程式(2)について考えます。
Ax =b ・・・・・ (1)
Ax =0m ・・・・・ (2)
前章の( m,n )行列 A の見方を少し変えてみるために,
y = Ax ・・・・・ (3)
つまり,
y1 = a11 a12・・・・ a1n x1 y2 a21 a22・・・・ a2n x2 : : : ・・・・・・ : ym am1 am2・・・・ amn xn
と書き換えます。すると,この式(3)を,n次元ベクトルx から,Ax を計算して得られる m次元ベクトル,y に対応させる写像,
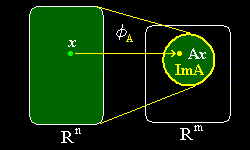
φA: x → y
とみなすことができます。
[2] もう少し,きちんと書くと,
| 定義 [行列による線形写像] n次元ベクトルx を m次元ベクトルy へ対応させる写像を, y = Ax で定義する。 ただし,x ∈ Rn ,y ∈ Rm ,A∈{行列(amn)} |
このような写像は線形写像と呼ばれます。 ここで,y =Ax ∈ Rm と書いてますが,x が定義域 Rn 全体を動いても y が値域 Rm の全体を動くとは限りません。たとえば,下の(4,3)行列で表される写像φA: x ∈R4 → y ∈R3 は,
y = Ax =
1 1 1 1 1 1 2 2 0 0 0 0
x y z w
= x+y+ z+ w x+y+2z+2w 0
= p 1 + q 0 (p=x+y+z+w,q=z+w ) 1 1 0 0
 と書くことができて,x,y,z,wが任意の実数をとるとき,p,q は独立に任意の実数をとれることに注意すれば,4次元ユークリッド空間の全体を3次元ユークリッド空間全体ではなく,その部分空間である2次元平面に移す写像です。つまり,写像φAの像の次元はAのみかけの行数,列数だけで決まるものでなく,その行列要素に依存して変化します。そこで,行列Aであらわされる線形写像の像,すなわち,
と書くことができて,x,y,z,wが任意の実数をとるとき,p,q は独立に任意の実数をとれることに注意すれば,4次元ユークリッド空間の全体を3次元ユークリッド空間全体ではなく,その部分空間である2次元平面に移す写像です。つまり,写像φAの像の次元はAのみかけの行数,列数だけで決まるものでなく,その行列要素に依存して変化します。そこで,行列Aであらわされる線形写像の像,すなわち,
ImA ≡ ImφA ≡ { Ax |x ∈Rn }
の次元を
dim ImA = rankA ( =rank φA ) [行列 Aの階数]
と書き,階数 (rank) と呼ぶことにします。つまり,階数とは,線形写像 φA の値域の次元です。
[3] では,この階数をどのように求めるのか考えていきましょう。いま,(m,n)行列 A の各列を括って縦ベクトルあらわし,
A = (a1 a2 ・・・ an ),; ただし,a1= a11 ,a2= a12 ,・・・・ ,an= a1n a21 a22 a2n : : : am1 am2 amn
と書くことにすると[#],y = Ax は,
y1 = a11 a12・・・・ a1n x1 y2 a21 a22・・・・ a2n x2 : : : ・・・・・・ : ym am1 am2・・・・ amn xn
= x1a11+x2a12+・・・+xna1n x1a21+x2a22+・・・+xna2n : ・・・・・ x1am1+x2am2+・・・+xnamn
= x1 a11 + x2 a12 +・・・+ xn a1n a21 a22 a2n : : : am1 am2 amn
つまり,
y = x1a1 + x2a2 +・・・・・+ xnan ・・・・・ (3)
と表せます。この最後の表現の右辺を n個のベクトル,a1,a2,・・・,an の1次結合といいます。ここで,x が Rn のすべてにわたるとき,その成分, x1,x2,・・・・・,xn はそれぞれ任意の実数値をとれることに注意してください。 そのとき, x1a1+x2a2+・・・・・+xnan によって表されるベクトル全体の集合を,{a1,a2,・・・,an } の張るベクトル空間と呼ぶことにしましょう[#]。
このように定義すると,
| A の階数 [ dim ImA ] = ”A の列ベクトルたち” {a1,a2,・・・,an } の張るベクトル空間の次元。 |
であることわかります。
(行と列を交換して同様な導出を行えば,A の行ベクトルの張る空間に等しいことも示せます。)
[4] さて,3次元ユークリド空間への ”直感” に基づいて,漠然と ”次元” という言葉をここまで繰り返し使ってきましたが,さらに先へ進んで行くために, ”次元” の厳密な定義を導入しておきましょう。
まず,1次独立という用語の定義からです[#]。r個のベクトル,a1,a2,・・・,ar が1次結合として,
p1a1+p2a2+・・・・・+prar = q1a1+q2a2+・・・・ +qrar ・・・・・ (4)
が成り立つならば,必ず,その係数(=実数)について,
p1=q1, p2=q2, ・・・・ , pr=qr
となるとき,a1,a2,・・・,ar は1次独立であるといいます。 もしくは,
x1a1+x2a2+・・・・・+xrar =0 であるならば,必ず, x1=x2=・・=xr=0 ( x =0r )
と言い直すこともできます[#]。 これは(4)を,
(p1−q1)a1+(p2−q2)a2+・・・+(pr−qr)ar =0
と書いて言い直したものです。
[5] 一方,1次独立でないとき,a1,a2,・・・,ar は1次従属である,といいます。つまり,一次従属ならば,すべてが 0 ではないある実数の組,{ x1,x2,・・,xr }が存在して,
0 = x1a1+x2a2+・・・・・+xrar
とできます。これらの用語を用いてベクトル空間の次元を次のように定義します。
|
定義 |
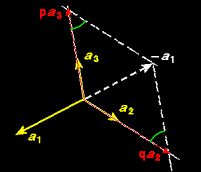 この定義は当然,ユークリッド空間の次元と整合性のあるものです。たとえば,平面内で平行(逆平行)でない2つのベクトルを選べば,x1a1+x2a2 が0 となるのは x1=x2=0 の場合だけですが,一方,どんな3つのベクトルを選んできても,x1a1+x2a2+x3an3 =0 となるような,すべてが 0 でない x1,x2,x3 の組を選べ出すことができます(右図)。
この定義は当然,ユークリッド空間の次元と整合性のあるものです。たとえば,平面内で平行(逆平行)でない2つのベクトルを選べば,x1a1+x2a2 が0 となるのは x1=x2=0 の場合だけですが,一方,どんな3つのベクトルを選んできても,x1a1+x2a2+x3an3 =0 となるような,すべてが 0 でない x1,x2,x3 の組を選べ出すことができます(右図)。
ついでに述べておくと,前章で示した連立1次方程式が唯一,1組の解を持つ条件[#]はこの用語を用いて,言い直すことができます。すなわち,
| Ax = b が唯一1組の解を持つ ⇔ 同次方程式 Ax =0 の解はx =0 のみ ⇔ a1,a2,・・・,an が一次独立 |
と言い表すことができます。特にAが正方行列であれば,この条件は「⇔ |A|≠0」とすることもできます。
[6] n次元ベクトル空間の n個の一次独立なベクトルの組,a1,a2,・・・,an をそのベクトル空間の基底とか基底ベクトルといいます。では,任意の行列A が与えられた時,具体的にどのようにしたら一つ,基底を見い出されるのでしょうか。答えは,連立1次方程式方程式の列に関する基本変形を行えばいいのです。
行列の基本変形とは,あるakに対して,p1a1+p2a2+・・・・・+pnan を加えることに相当しますが,a1,a2,・・・,an が一次独立であるならば,どんなp1,p2,・・・,pn を選んでもその結果が,ak→0 となることはありません。なぜなら,もし,そうであれば,p1a1+p2a2+・・+(pk−1)ak+・・・+pnan =0 となり,これはa1,a2,・・・,an が一次独立であることに反するからです。
一方,a1,a2,・・・,an が一次従属である場合は,適切なp1,p2,・・・,pn を選ぶことで,ak→0 とすることができます。
このような操作(基本変形)を繰り返していき,もうそれ以上,どの列ベクトルをとっても零ベクトル0 へ変形することができなくなったとき,「生き残った」0 ではないベクトルが,互いに一次独立なベクトルということになります。もちろん,その数は行列Aの階数です。
再び,2章で求めた解空間が直線となる連立1次方程式:
Ax =b
↓↑
2x−4y+3z =-3
4x−3y+3z = 1
6x−7y+6z =-2解 →
x = 13/10 + t -3/10 y 7/5 3/5 z 0 1
を例にとり,みてみましょう。
2 -4 3 4 -3 3 6 -7 6 1列×2を2列にたす
1列×(-3/2)を3列にたす
⇒
2 0 0 4 5 -3 6 5 -3 2列×(3/5)を3列にたす
⇒
2 0 0 4 5 0 6 5 0
このままでもいいのですが,1列を2で割った列ベクトルと,2列目を5で割った列ベクトル,
a1= 1 ,a2= 0 2 1 3 1
を ImA の基底にとることができ,
ImA = pa1+ qa2 ( ⇒ dim ImA = 2 )
と表されます。ここで,p,q は任意の実数です。したがって,行列 A の階数は2で,もちろん,連立一次方程式における独立な方程式の数と同じです。また,基底は一つのベクトル空間に対して唯一定まるものではなく,無数に存在することに注意してください。詳しくは基底変換のところで説明します。
[7] なお,連立1次方程式:Ax = b が解を持つ条件は,
-3 = b ∈ ImA 1 -2
でなければいけませんが,これはp=-3,q=7 とすれば良いことはすぐに確認できます。
[1] ここでは,前章で行列によって定義した線形写像をもっと一般性のある定義へと拡張します。まず,前章で定義した核,KerA を[#] 写像の言葉で定義しなおすことから始めます。すなわち,
「 KerφA :
写像φA:Rn → Rm によって,0m∈Rm に移ってくるすべての元∈Rn 」
と考えるのです。(右下図参照)
(注: 代数を学んだことのある人は核の定義を,
「 写像,φ:V ⇒ W において,Ker φ={v|v ∈V,φ(v)=0∈W }
とも定義される[#]ことを知っていると思いますが,これは上の定義の一般化です。)
「A の核:KerA = KerφA 」の重要な性質として次の3つが挙げられます。
|
ここで,0n∈Rn は要素がすべて 0 である Rn のゼロベクトルです。これらが成り立つことは具体的な確認(⇒)を見ればすぐにわかります。(1)は当たり前ですね。(2),(3)の性質は,「KerA がRnの部分集合として ”和,スカラーの行列演算”に関して閉じている」という言い方もします。
[4] また,連立1次方程式を次のようなRnからRmへの線形写像,
φA : x ⇒ b ; x ∈ Rn ,b ∈ Rm
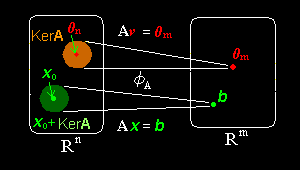 とみなせば,同次方程式(2)の解空間: KerA はφA によって,0m に写される原像全体の集合(n次元ユークリッド空間:Rn の部分集合)となっています。
とみなせば,同次方程式(2)の解空間: KerA はφA によって,0m に写される原像全体の集合(n次元ユークリッド空間:Rn の部分集合)となっています。
また,連立1次方程式(1)の解空間は,φA によってb に写される原像全体の集合であり,その特異解をx0 とすると,
x0 + KerA
[2] そして,KerA の上のような性質を一般化して, KerA→ V と書いた,
| (1)' 0 ∈V, (2)' x1,x2 ∈ V ⇒ x1+x2 ∈V (3)' x ∈V,λ∈ R ⇒ λx ∈V |
を満たす集合 V が(Rnの部分)ベクトル空間 の定義[#]となることに注意しましょう。これもここまで漠然と述べてきたベクトルの必要最小限の定義です。
(正しくは,この他にいくつかユークリッド空間ならば自明な性質をベクトル空間の定義に加える必要がありますが,それは線形代数入門[#]に譲り,ここは先へ進みます。)
[4] 一方,行列で表される写像,
φA(x ) ≡ Ax
については,行列とベクトルとの間で成り立つ算法:
A(x1+x2 )= Ax1+Ax2
A(λx ) = λAx
を一般化した性質,
| 線形写像の定義 (1) φ(x1+x2 )=φ(x1)+φ(x2) (2) φ(λx ) =λφ(x ) |
を抽出することができます。これをみたす写像を 線形写像 として定義することになります。 ( より詳しくは→[#] )
このように連立1次方程式の理論から”ベクトル空間”,”線形写像”というきわめて重要な概念が確立されます!