| 2 解空間 | ||
| f-denshi.com 最終更新日: 03/10/5 | ||
「はじめての線形代数」PDF版がこちらからダウンロードできます。
⇒ 無料見本
[1] 連立1次方程式の解の集合を解空間 (solution space) と呼びましょう。前章で見たように解空間は1点からなる集合(0次元)であったり,直線上の点の集合(1次元)であったりいろいろな空間となりえます。
さて,必ずしも未知数と独立な方程式の数が一致しない一般な連立1次方程式は(m,n)行列:A,m次元ベクトル:b ,n次元のベクトル:x を用いて,
Ax =b ・・・・・ (1)
A = a11 a12 ・・・・ a1n , x = x1 , b = b1 a21 a22 ・・・・ a2n x2 b2 : : ・・・・ : : : am1 am2 ・・・・ amn xn bm
と表わされます。その解のひとつをx0 とします。また,上式で,b =0m∈Rm とした方程式
Ax =0m ・・・・・ (2)
をこの連立1次方程式に付随する同次方程式(homogeneous linear equation ) と呼び,この(2)の解をv , その全体集合を,W ={v|Av =0m} とします。すると,連立1次方程式 (1) のすべての解を,
x =x0 +v ; (v ∈W )
と表すことができるのです。ここで,
x0 を特異解 (singular solution),
x0 +v ;(v ∈W ) を一般解(general solution ) ←(1) の解全体
といいます。証明は次のとおりです。
[2] x0 +v が(1)の解であることは,
A(x0+v ) = Ax0 + Av = b +0m = b
からわかります。(十分性)
逆に(1)の任意の解をy とすると, ( つまり,Ay =b を満たすy について考えると )
A(y −x0 ) = Ay −Ax0 = b−b = 0m
なる関係式から,(y −x0 ) は同次方程式(2)の解v です。つまり,
y −x0 = v ∈W ⇔ y =x0+v ;(v ∈W )
を満たさなければならないことがわかります(必要性)。 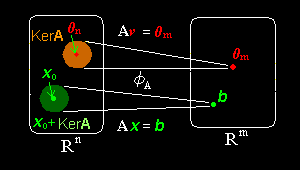
[3] このように同次方程式:Av=0m の解の集合は連立1次方程式(1)の解の集合の次元を決定する重要な集合で,核と呼ばれ,次の記号で表します。
KerA ≡W ={v|v ∈Rn,Av =0m}
また,KerA は n次元ユークリッド空間 Rn の部分集合です。
(右図の詳細は次章で説明します。)
以上まとめると,
| 定理 連立1次方程式: Ax = b ・・・・・ (*)の解は,x0 +KerA で与えられる。 ただし, x0 は(*)の解のひとつ, KerA は(*)に付随する同次方程式 Ax =0m の解である。 |
ここで,x0 は点,すなわち,0次元 なので,x0 +KerAの次元とKerAの次元が等しいことに注意してください。つまり,
「 連立1次方程式の解空間の次元は対応する同次方程式の解空間の次元と等しい。 」
ということです。
[1] 話が抽象的でしたので,連立1次方程式を解くという観点からもう一度,上の定理[#]を見直して理解を深めましょう。前章の不定解を持つことがわかっている連立1次方程式[1] [#]をもう一度書くと,
2x−4y+3z =-3
4x−3y+3z = 1
6x−7y+6z =-2⇔
2 -4 3 x = -3 4 -3 3 y 1 6 -7 6 z -2 ⇔ Ax = b [*]
答え →
x = 13/10 +t -3/10 y 7/5 3/5 z 0 1
一方,この連立方程式に付随する同次方程式は,
2x−4y+3z = 0
4x−3y+3z = 0
6x−7y+6z = 0実質的に ⇒ 2x−4y+3z = 0
5y−3z = 0
となりますが,この方程式の解はパラメーター t を用いて,
x = -3t/10 ≡v ; [ 同次方程式 Ax = 0 の解 ] = 直線 = KerA y 3t/5 z t
となり,連立1次方程式[*]がパラメータを含む不定解となる本質的なところはここにあります。一方,特異解が,
x = 13/10 ≡ x0 [特異解] y 7/5 z 0
であることは,これを[*]に代入して確かめられます。したがって,連立1次方程式[*]の解[一般解]は定理のとおり,
x = 13/10 +
t -3/10 3/5 1 y 7/5 z 0 [一般解] = [特異解] = [同次方程式の解]
となっていることがわかります。
[3] 解が一意的に決まる場合はどうでしょうか。
連立方程式[2]
2x−4y+3z =-3 ・・・・・ (1)
4x−3y+3z = 1 ・・・・・ (2)
6x−2y+4z = 6 ・・・・・ (3)[**] 答え ⇒
x = 1 y 2 z 1
まず,特異解はこの連立1次方程式の解そのもの
x = 1 = x0 y 2 z 1
です。また,[**]に付随する同次方程式は
2x−4y+3z = 0
4x−3y+3z = 0
6x−2y+4z = 0
ですが,その解は,
x = 0 =v y 0 z 0
です。したがって,解が唯一存在する場合も,
[一般解]=x0[特異解]+v[同次方程式の解]
が成り立っています。
[4] なお,ここで述べた同次方程式に関する事実は次のように一般化することができます。
連立1次方程式:
Ax = b ; A:( m,n )行列が唯一の解を持つとき,その同次方程式 Ax =0m の解は x = 0n のみである。 |
[5] 最後に連立1次方程式が実質的に
2x−4y+3z =-3
とひとつであらわせる場合を調べて見ましょう。付随する同次方程式,
2x−4y+3z = 0
の解は,2つのパラメーターを用いて,( y → s , z → t )
(4s−3t)/2 = 2 s + -3/2 t = v ⇒ [平面上の点全体] s 1 0 t 0 1
となります。一方,特異解は,
x = -3/2 = x0 [特異解] y 0 z 0
となります。したがってこの場合も
[一般解]=[特異解]+[同次方程式の解]
が成り立っており,一般解はR3内の平面(2次元空間)を表します。
以上,解空間が点(0次元),直線(1次元),平面(2次元)となる場合を具体的に調べてみました。
[1] 連立1次方程式の解をユークリッド空間内の部分空間 (subspace) として幾何学的に捉えて見ましょう。直感的に捉えられるのは未知数が3個以下の場合ですが,未知数4以上への拡張も容易に創造(想像?)できます。未知数3の連立1次方程式:
a1x+a2y+a3z = d1
b1x+b2y+b3z = d2
c1x+c2y+c3z = d3
を考えると,3つの方程式の一つひとつは3次元空間内の平面の方程式に対応していて,連立1次方程式の解はその3つの平面の共通部分に対応しています。
[2] いま,解がただ”1組”だけ存在する場合を考えると,与えられた方程式に対応する平面は下図の左のように適当な角度で交わっており,交点は赤い点で示す一点のみです。
連立1次方程式は先に示したような基本変形を施すことで最終的に,x=x0,y=y0,z=z0 という ”解が自明の連立方程式” にたどり着きます。また,この ”解が自明な連立方程式”
のひとつ一つはもちろん平面の方程式でもあり,各平面は各座標軸に直交しています。(下図の右)。
a1x+a2y+a3z = d1 [1]
b1x+b2y+b3z = d2 [2]
c1x+c2y+c3z = d3 [3]3元連立1次方程式
を解くとは?
=
赤い交点を中心に
平面を回転させて,
↓
各平面を座標軸に
直交させる
ということなんです!x = x0
y = y0
z = z0
これは連立方程式を解く過程で,たとえば,[3]式からz を消去すれば,交点を含むz軸に平行な平面 [3]’が得られるというような操作を続けてたどり着くことがわかります。すなわち,
| 連立1次方程式を解く ⇔ 平面(たち)を”交点”が変化しないように回転させて,各座標軸に直交させる |
と見ることができます。
[3] 解の集合が,”点”,”直線”,”平面”,”なし”となるときについての方程式を表す平面の位置関係を下にまとめました。
幾何学的配置 ケース1 ケース2 ケース3 ケース4 独立な方程式 − 3 2 1 解空間の次元 なし 0(点) 1(直線) 2(平面)
ところで,上の表を見ると,解が存在する場合は,
[ 独立な方程式の数 ] + [ 解空間の次元 ] = [ 変数の数 ]
が成り立っています。ここには何か法則が潜んでいるようです。実際,これは ( m,n ) 行列 A について成り立つ ”次元公式”(定理),
dim ImA + dim KerA = dimV ; x ∈ V
と呼ばれるものに対応しています。 この定理は4章[#]で説明します。