|
３ 剰余環 Znと有限体 Fp | |
| f-denshi.com 最終更新日： 21/7/28 | ||
| ［目次へ］ | ||
| サイト検索 | ||
第一部 群論 11，14 では整数の剰余類の集合 Zn について，加法群＋と乗法群 ×を別々に導入してそれぞれ考察しましたが，ここでは同時にこれら２種の演算を持ち込み，環，および（有限）体を構成します。
［１］ 整数の剰余類の集合：
Zn ＝｛[0]n，[1]n，［2］n，・・・，［n-1］n｝
を考えます。11．[#] で見たように Znは加法＋を演算として可換群をなします。この加群では，[0]n が零元となり，[a]n のマイナス元（逆元）は［n-a］n であたえられます。また，剰余類を乗法群とするために乗法×を定義することも可能で交換法則が成り立ちました。 さらに，この２種の演算の定義に基づいて，
[a]n×（ [b]n＋［c］n）＝[a]n× [b＋c］n
＝[a×（b＋c）］n
＝[a×b＋a×c］n
＝[a×b］n＋［a×c］n
＝[a］n×［b］n＋［a］n×［c］n
と，×，＋ についての分配法則が成り立つことがわかります。すなわち，
剰余類，Znは この×，＋の演算のもとで （ 1をもつ可換 ） 環である |
ことがわかります。これを整数の剰余環（整数環）と呼びます。
［２］ 整数の剰余類 Znのうち，n の倍数の集合（n）＝[0]n＝｛・・・-2n，-n，0，n，2n，・・・｝は整数のイデアルとなっていました[#]。
14．で見たように，
Zn* ＝ Zn −｛ [0]n ｝
＝ ｛ [1]n，［2］n，・・・，［n-1］n ｝
はn が素数 p であるとき，積 × のもとで群をなしました。これは環 Znで考えると，零元である [0]n 以外のすべての元が積に関して逆元をもつことを示しています。したがって，２種類の演算＋，× が定義されたもとで次の定理が成り立ちます。
| 定理 ［p 元体］ p を素数とすると，Zp ＝｛ [0]p，[1]p，［2］p，・・・，［p-1］p ｝ は ×，＋ の演算のもとで体となる。 |
この体（正確にはこれと同型な体）を整数の剰余体，有限体，ガロア体，またはｐ元体といいます。また，体であることを（2種類の演算を考えていることを）はっきり示すために体の英語，Field の頭文字をとって，Zp の代わりに以後，Fp と書くことにします。←整数の剰余群Zpと区別するためです。教科書によっては，GF(p)という記号も使われます。
また，これ以後，特に注意を促す必要があるときを除いて，［ ］pを省略して，
Zp ⇒ Fp ＝ ｛ 0，1，2，・・・，p-1 ｝
と表記することにしましょう。
［３］ 一般化しておきます。
| 定義 剰余環 環 R のイデアルを I とするとき，R 上の同値関係〜として， a〜b ⇔ a−b ∈ I ( ⇔ a〜b mod I )を定めて得られる同値類， [a] ≡ a＋ I ≡ { a＋r｜r ∈ I } ( ⇔ a mod I )の全体集合を R/ I と書き，この集合の元に次の演算， 和： [a]＋[b] ＝[a+b] （＝ a＋b＋I ）を導入すると，R/ I は環となるが，これを R の I による ( または I で割った）剰余環という。 なお，文脈から同値類であることが明らか場合は，[ ] を外して単に a とも書く。 |
［４］ 剰余環はイデアルの特徴によって，さらに整域であったり，体であったりします。
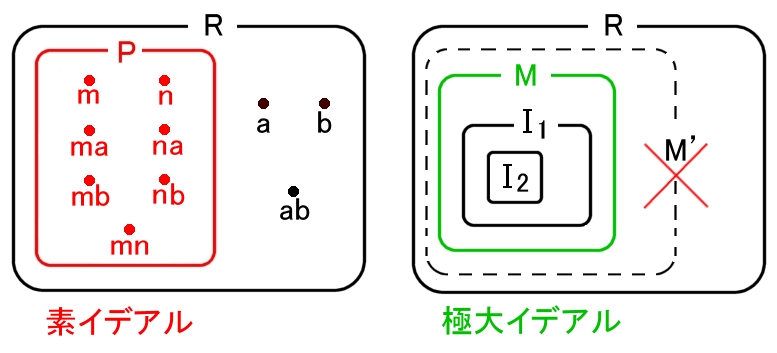
| 定理２ （１） P が環 R の素イデアルであることと， 剰余環 R/ P が整域であることは同値である。 （２） M が環 R の極大イデアルであることと， 剰余環 R/ M が体であることは同値である。(剰余体) |
pZは素イデアルであり，極大イデアルでもある。よって，Fp は体になることが分かります。
（１）の証明
(1) a，b ∈R，その剰余環を [a]，[b] とします。このとき，
[a]＝0 ⇔ a∈ I 待遇 ⇒ （ [a]≠0 ⇔ aI ） (1)
[b]＝0 ⇔ b∈ I 待遇 ⇒ （ [b]≠0 ⇔ b
また，素イデアルの定義 ： ab ∈ I ならば，a ∈ I または，b ∈ I の待遇は，
a
(2) すると，(1)，(2),(3) より，
[a]≠0 かつ，[b]≠0 ⇒ ( ab I ⇔ [a] [b]＝[ab]≠0 )
つまり，剰余環が零因子を持たないことが示された。
（２）は逆元の存在を示すことで証明される。
(1) R/Mの [0] ではない元 [a] 
M をとると，M と a から生成されるイデアル I ＝M＋(a) は，M が極大イデアルならば，I＝R である。
よって，R の任意の元は，m＋ar (m∈M，r∈R) と表される。もちろん，R の 1 も
1＝m＋ar
と表すことができる。
(2) この両辺 M による剰余を考えると，
[1]＝[ar]＝[a] [r]
この式から，[a] が逆元 [r] を持つことが分かる。
(3) 逆に R/M が体であるとする。I ⊃≠M である任意のイデアル I には，aM である元が存在して，[a] ≠ [0] ，かつ，逆元 [b] をもち，
[a] [b]＝[ab]＝[1] ⇒ 1−[ab] ＝ 0
これは，
1−ab ＝ m∈M ⊂ I
を意味するが，a∈ I なので，
1＝m＋ab ∈ I
であることを示している。言い換えると，I は，「 単位元 1 を含む部分イデアル＝R自身］であることを示している。
(4) そのためには，M は極大イデアルでなければならない。 （終）
| 定理 （１） 極大イデアルならば，素イデアルである。 （２） 単項イデアル整域においては，素イデアルならば，極大イデアルとなる。（１）の逆が成り立つ。極大イデアル ⇒ 素イデアル 素イデアル ⇔ 極大イデアル ［ ＰＩＤのとき ］ |
証明
環 R の極大イデアル M による剰余環 R/M は体であるので整域でもある。
したがって定理２の（１）より，M は素イデアルである。
| 定理 単項イデアル整域（PID） R の元 m が既約元であることと，(m) が R の極大イデアルになることは同値である。
|
証明
⇒ を示す。
(m) ⊂≠ I ⊆ R ･･･ [*]
であるような R のイデアル I を考えると，I ＝R となることを示せばばよい。
(1) R は単項イデアルなので，ある c が存在して，(c)＝I とできるが，そのとき，m∈ I なので，
m＝cr r∈R
と表すことができる。そして，m が既約元 [#] であれば，c，r のいずれかは単元 [#] である。
(2) このとき，r が単元だと (m)＝(c) となり，[*] に反するので，c が単元でなければならない。
(3) すると，単元から生成されるイデアル I ＝(c) は R自身 ということになる。つまり，(m)
より大きなイデアルは R しか存在しない。 (完）
逆 は，m＝ab （ a,b∈R ) と積で表したとき，必ずa，b のどちらかが単元でなければいけないことを示せばよい。
(1) イデアル (m) の元は，mr ( r∈R ) と表すことができるが，
mr＝abr＝a(br) ∈ (a)
これより，(m) が極大イデアルならば，(a)＝(m) または，(a)＝R のどちらかであると分かる。
(2) もし，(a)＝(m) ならば，単元 u を用いて，a＝um と書けるので，
m＝ab＝umb ⇔ m(1−ub)＝0
ここで，R は整域なので，mで最後の式を簡約すると，1＝ub となり，この式は b が単元でなければ成立しない。
(3) もし，(a)＝R ならば，1∈(a) なので，
r∈R が存在して，ar＝1 とできなければならないのだが，この式は a が単元でなければ成立しない。
(4) 以上より，m＝ab と書かれたときは，a，b のいずれかは単元であることが分かった。つまり，mは既約元である。
ここまでのいくつかの定理を組み合わせると，PID (体でもよい) の Rの部分環 M＝(m) が与えられたとき，
| mが既約元 ⇔ Mが極大イデアル ⇔ Ｍが素イデアル ⇔ 剰余環 R/M が体 (剰余体) |
であることが示されました。
［１］ 体 Fp ＝ ｛ 0，1，2，・・・，p-1 ｝ から零元を除いた集合を，
Fp* ＝｛ 1，2，・・・，p-1 ｝
とします。 Fp* には乗法として元の位数 [#] が p-1 の元 ｒ が少なくとも一つ存在することが証明できます（Apndex 1）。
すなわち，Fp*は積に関して巡回群で，r 自身をかけ合わせていけば，
r，r2，・・・，rp-2，rp-1＝1
が得られ，これら p-1個の元はすべて異なっています。このような元 ｒ を ｐ を法としての原始根といいます。
この r を用いれば，
Fp* ＝ ｛ 1，r，r2，・・・，rp-2 ｝
と表すことができます。したがって，r が与えられると， Fp* の任意の元 a は，
a ＝ rk
と書くことができ，各元をそれぞれ異なる k に一意的に対応させることができます。この k を 原始根 ｒ に関する a の指数 といい，
k ＝ind r（ a )
と書きます [#]。
［２］ F5 ＝ ｛0， 1，2，3，4 ｝について具体的に見てみると，
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| F5積表 | F5*累乗 rn |
上の表から，
Fp*＝｛ 1，2，3，4 ｝において，2 と 3 が p-1＝4 乗して初めて，1となるので，原始根であることが分かる。
さらに，原始根が2の場合は，
｛ 1，r，r2，r3 ｝＝｛1，2，4，3｝＝Fp*
原始根が3の場合は，
｛ 1，r，r2，r3 ｝＝｛1，3，4，2｝＝Fp*
であることが確かめられます。
指数 ind r（ a ) については，
n ＝ 0 1 2 3 4 2n ＝ 1 2 4 3 1 3n ＝ 1 3 4 2 1 4n ＝ 1 4 1 4 1 ↓
a ＝ 1 2 3 4 ind 2（a) ＝ 0 1 3 2 ind 3（a) ＝ 0 3 1 2
となります。
［２］ これは普通の対数 log と似た性質（ a ＝ rk ⇔ ” log ra ＝ k ” ） をもっていて，
|
Fp* の元 a，b に対して ind r（ab) ＝ ind r（ a ) ＋ind r（ b ) （mod p-1） |
が成り立ちます（証明略）。 ←指数の演算＋，× が ” mod p-1 ” でおこなわれるのはもちろん， ap-1＝１ に起因してます。
［３］ また，Fp* の元 a の位数 | a | と原始根 r に関する a の指数 ind r（a) との間には，次の関係があります。
｜a｜＝ （p-1） [ a の位数 ］ （p-1，ind r（a)）
F5*の原始根 r=3 に対する a=4 の指数は2ですが，
（5-1） ＝2 （5-1，ind 3（4）
と計算すれば，4の位数が2であると求まります。
F5*の原始根3に対する a=2 の指数は3ですが，
（5-1） ＝4 （5-1，ind 3（2）
と計算すれば，2の位数が4であると求まります。
［１］ ここで，関連した定理を一つ紹介しておきましょう。この定理はフェルマーの小定理と呼ばれています。
| フェルマーの定理 素数 ｐ で割り切れない整数 a に対して， ap-1 は ｐ で割ると余りは 1 である。 ⇔ ap-1≡1 （mod ｐ） |
証明 (p=2のときは明らかに成り立つので p＞2 とします。)
［２］ 有限体Fp を考えます。←もちろん p は素数です まず，a を p で割り切れない整数としたので，[a]p は [0]p に等しくないことに注意しましょう。
［３］ 次に，集合： Fp*＝Fp−｛ [0]p ｝ の （p-1）個の元，
｛[1]p，［2］p，・・・，［p-1］p｝ ＝ Fp*
と Fp* の元それぞれに， [a]p∈Fp* を掛けた集合，
[a]p×Fp*≡｛[a]p×[1]p，[a]p×［2］p，・・・，[a]p×［p-1］p｝
を考えます。この集合の（p-1）個の元は互いにすべて異なります。たとえば，もし，
[a]p×[1]p＝[a]p×［p-1］p ならば，⇒ [1]p＝［p-1］p
となって矛盾するからです。↑体は簡約ができるのでした。[#] したがって，
Fp* ＝ [a]p×Fp* ←集合として等しいことを言ってます。
です。
［４］ すると，この２つの集合それぞれについて，”すべての元のかけ合わせ（積）”を考えると，それらは等しく，次の等式が成り立ちます：
[1]p×［2］p×・・・×［p-1］p＝（[a]p×[1]p）×（[a]p×［2］p）・・・×（[a]p×［p-1］p）
＝[a]pp-1×（ [1]p×［2］p×・・・×［p-1］p ）
両辺を [1]p×［2］p×・・・×［p-1］p で簡約すれば，
[1]p ＝ [a]pp-1
つまり，mod p のもとでは， [a]pp-1 ＝ [ap-1]p なので [#]，
[1]p ＝ [ap-1]p ⇔ 「 ap-1 は p で割ると 1 余る整数」
と言うことがいえるのです。以上よりフェルマーの小定理が証明されました。
注意：
この定理は a を p−1 回掛け合わせて初めて 1 ( mod p ) となることを主張してるるわけではない。