
| 2 部分環・イデアル・部分体 |  |
|
| f-denshi.com 最終更新日: 21/7/27 | ||
| [目次へ] | ||
| サイト検索 | ||
[1] 部分群と同様に環,体においても部分環,部分体を考えることができます。群にならった定義としては,もともとの環,体と同じ演算規則のもとで,それらのある部分集合だけを考えたときにそれらがそれぞれ環,体となるもの(閉じている)と捉えることができますが,利便性から以下のように定義しておきます。
| [部分環]
環 (R,×,+) の部分環 S とは,R の空でない部分集合 S であり,任意の a,b ∈ S について, a+b, a−b, a×b ∈ S を満たすものである。 |
例えば,普通の足し算・かけ算のもとで偶数全体 (2Z) は整数全体 (Z) の部分環です。つまり,偶数どおしの和,差,積の結果はすべて偶数になります。
[2] 重要な部分環にイデアルがあります。イデアルとは,
| 定義 イデアル 環 R のイデアルは,環 R の部分環 I で,さらに, a ∈ I,r ∈ R ならば,常に ar,ra ∈ I [(両側)イデアル]を満たす。 |
環の任意の元とその環のイデアルに属する元との積はすべてイデアルに属します。このような性質を吸収律といいます。例としては,
「 偶数の集合は整数のイデアル 」
です。なぜなら,(1) (偶数)±(偶数)=(偶数),(2) (偶数)×(整数)=(偶数)だから。
より一般的には,「整数 n の倍数からなる集合 nZ ((n)とも書く) も整数のイデアル」 です。また,0 (零) と R 自身はどちらも R のイデアルですが,自明イデアルといいます。
環 Rの有限個の元 a1,a2,・・・,an の rk∈R を係数とする1次結合,
r1a1+r2a2+・・・+rnan
の全体はRのイデアルとなりますが,これをa1,a2,・・・,an で生成されるイデアルといいます。特に n=1 のとき,
| 定義 イデアルの中で環 R の元 a の倍数 ( a )= { ar|r∈R } からなるイデアルを a の生成する単項イデアル(または主イデアル)という。 |
整数のイデアル nZ (n=正整数) は単項イデアルです。
整域 R のすべてのイデアルが単項イデアルであるとき,この環を単項イデアル整域 (PID) [ principal ideal domain ],または主イデアル整域と言います。体は整域でもあるので,体に対してもPIDという用語をよく用います。
例
(1) 整数環は単項イデアル整域である。
(2) R上の多項式環は単項イデアル整域である。
| 定義 環 R のイデアルを I とするとき, a,b ∈R について, ab ∈ I ならば, a ∈ I または, b ∈ Iが成り立つとき,I を素イデアルという。 |
例 整数 p が素数ならば,pZ は素イデアルですが,p≠素数ならば素イデアルではありません。2・3=6 ∈ 6Z ですが,2 も 3 も 6Z に属しません。
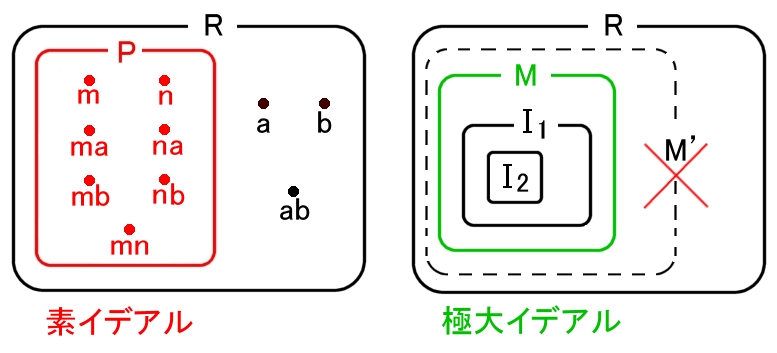
| 定義 環 R のイデアルを M とするとき, M ⊆ M’⊆ Rを満たすイデアル M’ が存在しないならば,M をRの極大イデアルという。 |
例
| 整数 p が素数ならば,pZ は整数環の極大イデアルである。 |
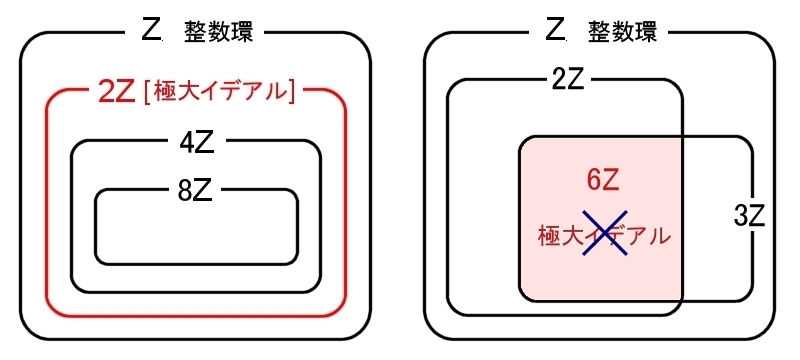
2ZはZの極大イデアルであるが,4Z,8ZはZの極大イデアルではない。
[6] 次に,体についての部分体・拡大体などの定義です。
| 定義 (1) 体 (F,×,+) の部分体とは,F の 0,1 を含む部分集合 K であり,任意の a,b ∈ K について, a+b, a−b ∈K, a×b ∈ K を満たし,さらに 0 でない K の任意の元に逆元が存在するものである。 (2) 体 F が部分体として F 自身しか含まないとき,体 F を素体という。(群の単純群 [#] に相当します。) K ⊃ M ⊃ F となっているとき,M を K と F の中間体であるという。 (4) K ⊃ F であるとき,K の部分集合 { α1,α2,・・・,αm } を含む最小の F の拡大体を F(α1,α2,・・・,αm) と書き,F に { α1,α2,・・・,αm } を添加して得られる拡大体という。 |
例
有理数体 Q は実数体 R の部分体であり,複素数体 C は実数体Rの拡大体であり,実数体は有理数体と複素数体の中間体である。すなわち,体として,Q ⊂ R ⊂C である。
| 定義 体 K が体 F の拡大体であるならば,K を F 上のベクトル空間[#] とみなしたとき,その次元を,F上の K の拡大次数といい,[ K:F ] と書く。 |
通常の複素数の演算の元で [ C:R ]=2 です。
任意の複素数は,x+yi ; i 2=-1,i ∈C ; x,y ∈R と表せますが,通常の複素数の演算(加法,スカラー倍)によって,複素数体は基底を 1 と i とする実数上の2次元ベクトル空間とみなせます。
一方,[ R:Q ] = ∞ です。拡大次数<∞ である拡大 K/F を有限次拡大,K を F の有限次拡大体という。
[8]
| 命題 体 F の有限次拡大体を M,さらに M の有限次拡大体を K とするとき,F から K への体の拡大は有限次拡大で, F上の K の拡大次数 [ K:F ] は次式で与えられる。 [ K:F ] = [ K:M ] [ M:F ] ( K ⊃ M ⊃ F )ただし, [ K:M] は M上の Kの拡大次数,[ M:F ] は F上のMの拡大次数である。 |
証明は
M 上のベクトル空間 K の基底を,α1,α2,・・・,αm
F 上のベクトル空間 M の基底を,β1,β2,・・・,βn
とするとき,
「F 上のベクトル空間 K の基底が,独立なmn個のベクトルαjβk ( j =1,2,…,m ; k =1,2,…,n )」
で与えられることを示す。
M上の Kの元は,aj∈M として,
=a1α1+a2α2+・・・,amαm
x= ajαj
と表し,F上の Mの元 aj は,cjk∈F として,
aj= cjkβk
と表す。これを先の式に代入してajを消去すれば,
x= cjkαjβk
これは F上の元 cjk と基底 αjβk を用いて K 上の元を表している。そして基底の数は mn 以下である。
αjβk ( j =1,2,…,m ; k =1,2,…,n )が1次独立であることは,
cjkαjβk=0
であれば,cjk=0 ( j=1,2,…,m ; k=1,2,…,n ) でなければいけないことを示せばよい(演習)。
[9]
| 例 ω | ,α= |
|
を添加する場合,すなわち,体の拡大 |
Q ⇒ Q(ω,α) ただし,ω2+ω+1=0
を考えてみましょう。
1つ目の拡大 Q ⇒ Q(ω)は2次拡大で,基底として 1,ω をとれます。
2つ目の拡大 Q(ω) ⇒ Q(ω,α) は3次拡大で,基底として,1,α,α2 をとれます。
したがって,全体としての拡大 Q ⇒ Q(ω,α) は6次の拡大で,基底は,
1,α,α2 ,ω,ωα,ωα2
となります。
| 定義 環 R の分数体(商体ともいう)とは,R (もしくは R と同形な部分環) を含む体 K で,K の任意の元が,r/u ( r,u ∈ R,u≠0 ) と分数の形に書かれるものをいう。 |
例
(1) 有理数体 Q = 整数環 Z の分数体
(2) 有理関数体 = 多項式環 F[x] [#]の分数体を F(x) と書きます。
(3) Fp(x) の不定元 x を x2 と置き換えた有理関数体 Fp(x2) は Fp(x) の部分体である。
Fp(x) ⊃ Fp(x2)
[11] 最後に,証明抜きで次の定理を述べておきます。
| 定理 整域 [#] はすべて分数体をもつ。(=分数体を構成することができる。) |