| 8 ガウスの定理 | |
| f-denshi.com [目次へ] 最終更新日:06/07/13 | |
| サイト検索 | |
ある状況下では,体積積分を面積分に置き換えることができます。
| ガウスの定理 3次元ユークリッド空間の有界な領域をV,その境界面を S とする。この閉領域で定義されたベクトル関数A (x,y,z) について, 成分表示: ここで, A =(A1,A2,A3)=(A1(x,y,z),A2(x,y,z),A3(x,y,z)) および, n =(cosα,cosβ,cosγ) 単位法線ベクトル: dS=n dS 面積ベクトル とする。もちろん,α,β,γ は,x,y,z の関数で,α(x,y,z),・・と書くべきもの。 |
定理の物理的意味は,Appendix2:四面体のガウスの定理 を参考のこと。(←こちらの内容の方が証明を追うよりもずっと有益!)
[1] この定理は,個別に成り立つ次の3つの式の和と考えることができます。
∂A1 dV= A1cosαdS ・・・(1) ∂x
∂A2 dV= A2cosβdS ・・・(2) ∂y
∂A1 dV= A3cosγdS ・・・(3) ∂z
[証明]
考え方を示すのには領域V の内部から見て境界が外へ向かって凸になめらかな右下のような立体図形を考えれば十分でしょう。 この図形の表面積Sは法線ベクトルのn の x 成分が0 である閉曲線C(図中の青い曲線)によって,S1 と S0 とに分けることができます。さらに,この立体を適当な y=一定,z=一定 の面で切り刻んで得られる細い柱の集合に分割し,その一本を取り出して拡大したものが下の柱です。この柱の左端面は必ずS1の一部であり,右端面は必ずS0の一部であることに注意して下さい。
さて,(1)の左辺の積分: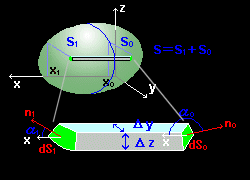
∂A1 dV ∂x
を累次積分とみて,まず,x について積分すると,
∂A1 dx=A1(x1,y,z)−A1(x0,y,z) ∂x
より,
I = ∂A1 dxdydz = A1(x1,y,z)dydz− A1(x0,y,z)dydz ∂x
となります。
[2] 一方,柱の曲面での単位法線ベクトルを左端(面積:dS1)で,
n1=(cosα1,cosβ1,cosγ1)
右端(面積:dS0)で,
n0=(cosα0,cosβ0,cosγ0)
とすると,0≦α1<π/2,π/2 ≦α0≦π に注意すれば,
dS1・cosα1 = dydz (左端面)
−dS0・cosα0 = dydz (右端面)
と変数を置き換えられます。すると,残りの2重積分は
I = A1 cosα1dS1+ A1 cosα0dS0
積分範囲を一つにまとめて閉曲面S上の積分として表記すれば,
= A1cosαdS
と(1)式が得られます。同様に,y 軸,z 軸に平行な面で分割された柱を考えれば,(2),(3)が得られ,3式をすべて足し合わせれば,ガウスの定理となります。
| ガウスの定理の系 (I) 勾配定理 [スカラーに関するガウスの法則] (II) グリーンの第1等式 (III) グリーンの第2等式
(V)
ここで,形式的な記法ですが,
と法線ベクトルの微分(方向微分係数[#])として表記しています。 |
[1]簡単に証明しておきます。
( I ) ガウスの定理において,A = (φ,φ,φ) とすれば,(1)式は,
∂φ dV= φcosαdS ・・・(1)’ ∂x
となります。(2),(3)式からも同様な式が得られ,それらをベクトルで表記すると,(I)となります。
( II ) ガウスの定理でA = φ∇ψとすれば,
∇・(φ∇ψ)dV= (φ∇ψ)dS
そして,左辺は分配法則を用いて,∇(φ∇ψ) = ∇φ・∇ψ+φ∇2ψ と変形すれば,(II)式となる。なお,これは,1変数の部分積分の3次元への拡張です。
↓↑比較せよ
(φ∇2ψ )dV = φ dψ dS− ∇φ・∇ψdV [3次元] dn
(φ・ψ'')dx = φ・ψ' − (φ'・ψ') dx [1次元]
(III) ガウスの定理で A =φ∇ψ−ψ∇φとしたもの。左辺は,
∇(φ∇ψ−ψ∇φ) =∇φ∇ψ+φ∇2ψ−∇ψ∇φ−ψ∇2φ
= φ∇2ψ−ψ∇2φ
と変形。
(IV) x 成分について示します。ガウスの定理において,
A = (0,A3,0),および,A = (0,0,A2)
とおくと ,(残りの変数については「ガウスの定理」と同じ記号を使って,)
∂A3 dV= A3cosβdS ∂y
および,
∂A2 dV= A2cosγdS ∂z
を得ます。辺々引くと,
∂A3 − ∂A2 dV= (A3cosβ−A2cosγ)dS ∂y ∂z
他の成分も同様に,
∂A1 − ∂A3 dV= (A1cosγ−A3cosα)dS ∂z ∂x
∂A2 − ∂A1 dV= (A2cosα−A1cosβ)dS ∂x ∂y
これらを順に成分とするベクトルをベクトル積を用いて表すと(IV)式となる。
(V) ( I )式において,φ ⇒ ∇φ とおけばよい。右辺は,
(∇φ)ndS = n ・∇φ dS
= dφ dS dn
| (1) ベクトル場 A =∇×B なるB が存在すれば,
divA =0 |
(divA =0 のとき,ベクトル場A を 湧き出しのないベクトル場 といいます。また,B をA のベクトルポテンシャルといいます。)
(証明) 公式1の(2)より,
divA =∇・(∇×B )=(∇×∇ )B =0
実は,この逆も成り立つ。証明は演習。
(2) divA = 0 ならば,スカラー関数φについて,
|
(証明) まず,
∇・(φA ) =A ・∇φ+φ∇A= A ・∇φ
これから,
A ・∇φdV = ∇・(φA )dV
ガウスの定理を用いて,
= (φA )・ndS
応用例
電磁気学 ガウスの法則 [#]
|
ベクトルポテンシャルの存在条件 divA =0 ならば,A =∇×B なるB が存在する。 |
証明
ベクトルポテンシャルB を具体的に構成してみせるために,
∂F1 =A1, ∂F2 =A2 ∂z ∂z
を満たす。F1,F2を成分とするベクトル,
F = ( F2,−F1,0 )
を考える。(この成分の順番や符号は,次に回転をとられることを考慮して。)
この回転を計算すると,
rotF = ∂F1 , ∂F2 ,− ∂F1 − ∂F2 ∂z ∂z ∂x ∂y
= A1,A2,− ∂F1 − ∂F2 ∂x ∂y
= A1,A2,A3 − 0,0, ∂F1 + ∂F2 +A3 ∂x ∂y
= A− 0,0, ∂F1 + ∂F2 +A3 ∂x ∂y
さらに,この発散をとると,
0 =div rotF
= divA−div 0,0, ∂F1 + ∂F2 +A3 ∂x ∂y
ここで,仮定より,divA=0 なので,
∂ ∂F1 + ∂F2 +A3 = 0 ・・・・・[*] ∂z ∂x ∂y
が成立することがわかる。さらに,F の修正項として,関数G(x,y,z)を成分とするベクトル,
G =(0,G,0)
を考え,この回転をとると,
rotG= − ∂G ,0, ∂G ∂z ∂x
これを先ほどのF の回転と足し合わせれば,
rot ( F +G )= A1− ∂G , A2 , ∂G − ∂F1 − ∂F2 ・・・・・[**] ∂z ∂x ∂x ∂y
これがAに等しくなるためには,まず,
∂G = ∂F1 + ∂F2 +A3 ∂x ∂x ∂y
のように定めれば,[**]の第3成分はA3とすることができます。そのとき,[*]に注意すると,
∂ ∂F1 + ∂F2 +A3 = ∂ ∂G = ∂ ∂G =0 ∂z ∂x ∂y ∂z ∂x ∂x ∂z
特に,
∂G =0 ∂z
とGを選ぶことが可能です。(実は最初からGをx,yのみの関数G(x,y,z0)とおいてもよかった!)そのとき,
rot ( F +G )=(A1,A2,A3)=A
したがって,B≡F+G=(F2,G−F1,0) はA のベクトルポテンシャルとなっている。(ただし,これが唯一というわけではない!)
具体的には,
F1= z A1(x,y,z)dz z0
F2= z A2(x,y,z)dz z0
G= x A3(x,y,z0)dx x0
とおけばよいことは容易に確かめられます。