| 4 行列の対角化が可能な条件 | ||
| f-denshi.com [目次へ] 最終更新日: 21/08/30 図を追加 | ||
| サイト検索 | ||
[1] いよいよ,2.の懸案事項であった「行列が対角化可能であるための条件」を求めます。まず,「対角化可能」の厳密な定義から。
|
対角化の定義: ベクトル空間V上の線形写像Tの表現行列T が対角化可能であるとは,ある正則行列Pによって, P-1TP=D [D:対角行列] と表せることである。 |
とします。ここで,Pはベクトル空間Vの基底変換の行列 [#]です。対角可能とは,「うまく基底を選びなおしてやる,つまり座標変換してやる[#]ことで,V上の線形写像の表現行列を対角行列にできる」ことを言うのです。
一般的に,基底の変換を相似変換といい,「T と D とは相似である」といいます。この用語は D が対角行列でない場合でも用いられます。
ここで,相似の意味は,「基底の取り方が違うだけ(=成分を並べた表現行列が違って見えるだけ)で数学的な内容 (=線形写像として) は同じだ」ということです。
[2] いま,Tの固有多項式を,
ΦT(λ)=(λ−λ1)d1(λ−λ2)d2 ・・・ (λ−λm)dm
とします。すなわち,異なる λ1,λ2,・・・,λm の固有値をもち,それぞれの重複度は,d1,d2,・・・,dm であるとします。
この記号,用語のもとで,これから証明すべき定理を述べると,
| 定理1 ベクトル空間V上の線形写像Tが対角化可能である必要十分条件は,Tの各固有値λkの固有空間E(λk)に対して, dimE(λk)=dk が成り立つことである。 |
つまり,各固有値に対して,その固有空間の次元とその固有値の重複度が等しいければよいのです。
特に,固有方程式:ΦT(λ)=0 が重根をもたなければ,つまり,相異なる固有値をVの次元と等しいn個持っている Tは対角化可能なことは直ちにわかります。では,定理の証明です。
[証明] 必要性:
[3] ステップ 1
| 「線形演算子Tが対角化可能」 ⇒ 「T は1次独立なn個の固有ベクトルをもつ」 |
ことを示します。
Tが対角化可能ならば,ある基底変換の行列 (正則行列),
P=(p1,p2,・・・,pn) [#] が存在して,P-1TP = D
[ D: 対角行列で対角成分は,μ1,μ2,・・・,μn ]
とかけます[#]。この式の左から P をかけると,TP=PD,これを成分で書くと,(P-1はP の逆行列)
TP=(Tp1,Tp2,・・・,Tpn)
PD=(p1,p2,・・,pn) μ1 0・・・・・0 0 =(μ1p1,μ2p2,・・・,μnpn) 0 μ2 0・・0 0 0 ・・・・・0 μn
赤で示した行列の各列をおのおの比較すれば,
Tpj=μjpj (j=1,2,・・・,n)
これは行列T の固有方程式であり,固有ベクトルがpj,対応する固有値がμj( j=1,2,・・・,n )であることを示しています。さらに,P が正則である[#]ことから,|P|≠0,すなわち,p1,p2,・・,pn が1次独立であることもいえます[#]。したがって,このV上のn個のベクトルは,n次元ベクトル空間V を張ることができます。
(注意: p1,p2,・・,pn が1次独立でも固有値μkがすべて相異なるとは限りません。また,μkはλ1,・・・λmのいずれかに相当しています。)
[4] ステップ 2
ここで,n個の1次独立な固有ベクトルp1,p2,・・,pn を固有値が等しいものどおし集め,次のように記号を改めます。
λ1 : p(1)1,・・・,p(1)d1 : d1個 (=固有値λ1の重複度)
λ2 : p(2)1,・・・,p(2)d2 : d2個 (=固有値λ2の重複度)
・・・・・・・・・
λm : p(m)1,・・・,p(m)dm : dm個 (=固有値λmの重複度)
(もちろん,すべての固有値が異なれば,d1=d2=・・・=dm=1)
ここでの操作はn個の1次独立な固有ベクトルpj を並び替えただけなので,ベクトル p(i)j の全個数はn個 で,
n =d1+d2+・・・+dm ・・・・・・・・・・・ [*]
が成り立ち,基底:
{p(1)1,・・・,p(1)d1,p(2)1,,・・・,p(2)d2 ,・・・,p(m)1,・・・,p(m)dm }
で,n次元ベクトル空間 V を張ることができます。また,各固有空間E(λk)には少なくとも1次独立なdk個のベクトル{p(k)1,・・・,p(k)dk}を含んでいるので,その次元について,
dimE(λk)≧dk
でなければいけないことがわかります。ところが,前ページで示したように,dimE(λk)≦dk なので [#],結局,
dimE(λk)=dk
が成り立ちます。(必要性の証明終わり)
なお,[*] は次のように書き換えた方が便利。
dimV = dimE(λ1)+dimE(λ2)+・・・+dimE(λm) ・・・ [**]
|
[5] 十分性の証明の前にちょっと,気のきいた言い方を紹介しておきましょう。 上で成り立っているような E(λ1),E(λ2),・・・,E(λm) と V との関係を, 「 T の固有空間: E(λ1),E(λ2),・・・,E(λm) によるV の直和分解 」 ← 直交分解[#]とは別です。 と呼び,
と書きます。もっと一般的に書く (定義する) と,V の部分空間,W1,W2,・・・,Wm があって, (1) 各Wkがそれぞれ独立した異なる空間を張っている。 の両方が成り立つことをいっています。 この用語を使うと,定理1は次のように言い直されます。
・・・ 以上。 |
十分性:
[6] 十分性の証明です。さっそく上で定義した用語を使いましょう。[**]が成り立つということは,すなわち,
Tの固有空間:E(λ1),E(λ2),・・・,E(λm) によって,V が直和分解されていることです。このとき,各固有空間の基底を
E(λ1)の基底:Σ1={e1,・・・,es}
E(λ2)の基底:Σ2={es+1,・・・,es+t}
・・・・・・・・
E(λm)の基底:Σm={ev+1,・・・,ev+u}
ただし,s+t+・・・+u=n であり,合計 n個のベクトル,
{e1,・・・,es ,es+1,・・・,es+t,・・・,ev+1,・・・,ev+u}
は互いに1次独立であり,ベクトル空間V の基底になっているとします。
[8] すると,このn個の基底ベクトル(縦ベクトル)をこの順に並べて作った行列,
Q ≡(e1,・・・,es ,es+1,・・・,es+t,・・・,ev+1,・・・,ev+u )
は正則です。このとき,TQを計算すると,
TQ =(Te1,・・・,Tes,Tes+1,・・・,Tes+t,・・・,Tev+1,・・・,Tev+u )
=(λ1e1,・・・,λ1es,λ2es+1,・・・,λ2es+t,・・・,λmev+1,・・・,λmev+u )
| =(e1,・・・,es ,es+1,・・・,es+t,・・・,ev+1,・・・,ev+u ) |
|
||||||||||||||||||||||||||||||||||||||||||
= QD
となります。 ここで,Dは対角成分として,
E(λ1)の固有値λ1が s個
E(λ2)の固有値λ2が t個
・・・・・・・・
E(λm)の固有値λmが u個
が左上から順に並んだ対角行列です。Q は正則行列なので,Q-1を上式の左からかけて,
Q-1TQ=D
となり,これはQによりTが対角行列Dに変換できることを示しています。 つまり,[**]であるならば,T が対角化可能であること [十分性] が示されました。
(証明終)
ここまでの議論はざっくりとした一般論,概念的な話で,次ページから具体的なテクニックも含んだ内容に切り込んでいきます。
↓ 下図で全体像を掴んでいた方がモヤモヤしなくて済むかもしれません。
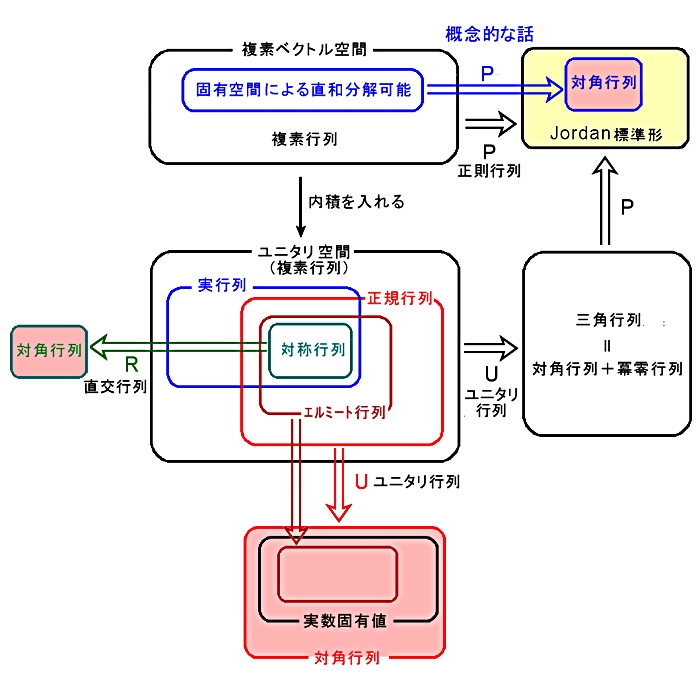
補足:
べクトル空間 V は固有空間によって直和分解される。 (次元については何も言えない・・。)
|
x1∈E(λ1),x2∈E(λ2),・・・,xm∈E(λm)のとき, x1+x2+・・・・+xm=0 ・・・・・・ (h1) ⇒ x1=x2=・・・・=xm=0 |
証明:
j = 1,2,・・・,m に対して,
Txj=λjxj
なので,(h1)に T を左からかけて,
Tx1+Tx2+・・・・+Txm
=λ1x1+λ2x2+・・・・+λmTxm =0
(h1)に λ1を左からかけて,
λ1x1+λ1x2+・・・・+λ1Txm =0
辺々引くと,
0 +(λ2−λ1)x2+(λ3−λ1)x3+・・・+(λm−λ1)xm =0 ・・ (h2)
再び,T を左からかけて,
(λ2−λ1)Tx2+(λ3−λ1)Tx3+・・・+(λm−λ1)Txm
=(λ2−λ1)λ2x2+(λ3−λ1)λ3x3+・・・・+(λm−λ1)λmxm = 0
(h2)からλ2を左からかけて,
=(λ2−λ1)λ2x2+(λ3−λ1)λ2x3+・・・+(λm−λ1)λ2xm = 0
辺々引いて,
0 +(λ3−λ1)(λ3−λ2)x3+・・・+(λm−λ1)(λm−λ2)xm =0 ・・・・ (h3)
これを繰り返すと,
(λm−λ1)(λm−λ2)・・・(λm−λm-1)xm =0
ここで,係数は0でないので,xm =0 であることがわかりました。 さらに,
x1+x2+・・・+xm-1=0
について同じように繰り返せば,xm-1=0 が証明でき,これを繰り返せば,
xm=0,・・・,x2=0,x1=0
であることが証明できます。