
| 5 剰余環と剰余体 |  |
|
| f-denshi.com 最終更新日: 21/08/01 | ||
| [目次へ] | ||
| サイト検索 | ||
[1] 整数環 Zについて n∈Z を選んで整数の剰余環 Znを得たように,体 F上の多項式環 F[x] についても元 f ∈ F[x] を選んで,多項式の剰余環 を得ることができます。すべての F上の多項式 h(x) は, f(x)が与えられると,q(x),r(x)∈F[x] ; (deg r(x) <deg f(x)) を用いて,
h(x) = q(x)f(x) + r(x) ⇒ 例 x3+2x2+5x+3 = (x+1) (x2+x+1)= 3x+1
と一意的に表せます。したがって,整数の剰余類に倣って f による多項式の剰余類を
[r(x)]f または r(x) + ( f )
と書きましょう。 ここで,(f) は f (x) の倍数で,
( f )={ f(x) ・ g(x)|g(x)∈F[x] }
です。 これは,例えば,f = x2+1 (2次式) をとれば,任意の多項式 h(x)∈Q[x] は
h(x) = q(x)(x2+1)+ ax+b ; ( a,b∈Q,q(x)∈Q[x] )
と書くことができて,剰余は1次式 ax+b となることを言ってます。 ←高校生でやりましたね。
[2] 整数の n による剰余類の代表元に 0 から n-1 までの整数を選べたように,代表元 r(x) は,次数 (deg f(x)−1) 以下の多項式を選ぶことができます。そして,多項式全体の集合 F[x] は類別されて,
F[x] = { r1(x)+(f) } ∪ { r2(x)+(f) } ∪ ・・・ ∪ { rn(x)+(f) } ∪ ・・・
= { [r1(x)]f ∪ [ r2(x)]f ∪ ・・・ ∪ [rn(x)]f ∪ ・・・
となります。ただし,整数の類別の場合は類別の個数は n個と有限ですが,多項式の場合は無限個となっています。
多項式の剰余類の演算の定義]
[r1(x)]f ±[r2(x)]f = [r1(x) ± r2(x)]f と定義すれば,剰余類 [r(x)]f の集合は環になる。 これを剰余環 F[x]/(f) と書く。 |
ただし,[r1(x) ・ r2(x)]f は deg r1(x)・r2(x) > deg f(x)−1 ならば,
r1(x)・r2(x)= q’(x)f(x) + r12(x)
と一意的に書けることを利用して,次数 (deg f(x)−1) 以下の多項式に代表元を帰着させることにします。
[3] 特に,f ∈ F[x] が既約ならば,次の定理が成り立ちます。
| 定理 [*] f ∈ F[x] が既約 (多項式) ならば剰余環 F[x]/(f) は体である。 これを f による剰余体といい,Ff と書く。 |
( f )={ f・g(x)|g(x) ∈F[x] }≡ I [倍数]
は F[x] のイデアル[#] となることに言及しておきましょう。
例えば,f=x2+1,g1(x),g2(x),h(x) ∈F[x] とすると, g1(x)±g2(x),g1(x)h(x)∈F[x] に注意して,
(x2+1)g1(x), (x2+1)g2(x)∈ I
⇒
(x2+1)g1(x)±(x2+1)g2(x)=(x2+1)(g1(x)±g2(x)) ∈ I
(x2+1)g1(x)・h(x)=(x2+1)(g1(x)h(x)) ∈ I
が示されるからです。すなわち,
| 命題 体 F上の多項式環を F[x] とすると, (1) 任意の f ∈ F[x] の倍数の集合 ( f ) は F[x] のイデアルである。 |
すると,定理 [*] の証明は ⇒ イデアルの性質 [#] と [#] からすぐわかることです。
他にもイデアルとしての次の特徴があります。
|
・ 特に 0 でない定数 c (∈F⊂F[x] ) の倍数 ( c ) はイデアルとなり,( c ) = F[x] ・ g,h∈F[x] のとき,( g ) = ( h ) である。 ⇔ g = rh なる可逆元 r が存在する。 ・ 多項式環は単項イデアル環である。 |
このように整数環から整数の剰余環への写像と多項式環から多項式の剰余環への対応=写像には,イデアルを介して共通の概念が含まれています。
特に,「イデアルは,環の準同型写像の核である。」とまとめられることが次の2.で示されます。
整数環 多項式環 整数の剰余環 多項式の剰余環 整数 n の倍数 ( n ) 多項式 f の倍数 ( f ) 素数 既約多項式 [a]n [r(x)]f
[1] 群論における準同型写像[#]と同じように環についても準同型写像を定義します。
| 定義 R,R’ を 1 をもつ可換環とする。写像 μ: R → R’ が環の準同型(写像)であるとは, 任意の a,b ∈ R, 1 ∈ R, 1’∈ R’ に対して (1) μ(a±b)=μ(a)±μ(b) を満たすことである。 ただし,+,・ は環 R 上の演算,+,・ は環 R’上の演算とする。 |
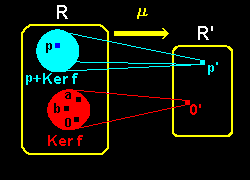
[2] さて,環準同型写像μ によって 0’∈R’に写ってくる元像,{ x∈R|μ(x)=0’,0’∈R’}を, Ker μ と書き,核と呼びます。
核は R のイデアルである
ことは次のように示せます。
まず,a,b ∈ Ker μ ならば,
0’=μ(0)=μ( b-b )=μ(b )+μ(-b )= 0’+μ(-b ),
すなわち,
μ(-b ) = 0’
したがって,
μ( a-b ) =μ(a)+μ(-b)= 0’+0’= 0’
μ( a+b ) =μ(a)+μ(b) = 0’+0’= 0’
μ( ab ) =μ(a)μ(b)= 0’・ 0’= 0’
これより,a-b,a+b,ab ∈ Ker μ なので[#] ,
(1) Ker μ は R の部分環である。
さらに,任意の元 r ∈ R に対して,
μ(ar ) =μ(a )μ(r )=0’・μ(r ) = 0’
 より
より
(2) ar ∈ Ker μ ( a ∈ Ker μ ,r ∈ R )
です。つまり,Kerμ はR のイデアルです。
さらにμ(p )= p’ ならば,
μ(p+Ker μ ) = μ(p )+μ(Ker μ ) = p’+0’
= p’
となり,p+Ker μ が一団となってp’に移されます。この様子を右に示しました。
[1] F(α) を体 F の代数拡大体とするとき,多項式環 F[x] の中でαを根に持つ次数が最小である多項式 φ(x) を,αのF上の最小多項式といいます。体上の多項式では議論の本質を変えないで,モニックな多項式に最小多項式を限定することもできます。
例 Q(√2) については,「√2 の最小多項式φ(x) は x2−2 」で,その次数は 2 です。
h(x)=(x2−2)(x2+x+1) ≡φ(x)g(x) ∈ (φ(x))
も Q(√2) 上に根 √2 を持ちますが,次数が 4 なので最小多項式ではありません。
(φ(x)) をφ(x)と任意の多項式∈F[x]との積によって生成される多項式全体とすると,それらはφ(x)で割り切れるだろうと予想できます。
すると,容易に次の定理が成り立つだろうことは推測できます。
[2]
|
定理 (2) αのF上の最小多項式φ(x) は,多項式環 F[x] において既約である ( = F上の既約多項式である)。 最小多項式 ⇒ 既約多項式 |
証明
(1) F[x] の元 f(x) に対して,x にαを代入した値 f(α) を対応させる F(α) の中への写像,
Φ: F[x] ⇒ F[α] ( ⊆ F(α) ) ←F にαを添加した拡大体
は環準同型写像となる。 ここで, ImΦ を F[α] と書いた。
(2) 単項イデアル整域 [#] である F[x] の元の中に,イデアルKerΦを生成する元 g(x) (もちろん,g(α)=0 を満たす) が存在して, (g(x)) =KerΦ が成り立つ [#]。
(3) 最小多項式はφ(α)=0 なので,φ(x)∈KerΦ=(g(x))
⇔ 生成元である g(x) はφ(x) を割り切る。 g(x)|φ(x)
ところが,φ(x)はαを根に持つ多項式の中で次数が最小であるから φ(x)=g(x) でなければいけない。
(4) したがって,KerΦ=(φ(x))
⇔ αを根にもつ任意のF上の多項式 (=KerΦ) はφ(x)で割り切れることが示された。 (終)
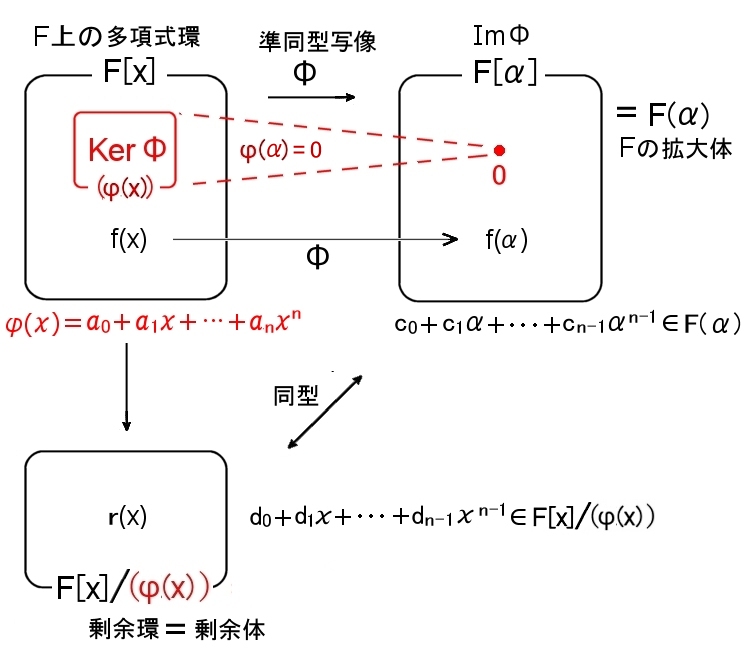
(5) 次に,F[x] と準同型写像 Φの KerΦ=(φ(x)) に準同型定理 [#] を適用すると,
F[x]/(φ(x))≡F[α] (体同型である)
(6) すると,F[α] は零因子を持たない整域 (体) なので,これと同型な F[x]/(φ(x)) も整域 (体) である [#]。
(7) よって,(φ(x)) は F[x] の素イデアルであり,極大イデアル ←定理 [#]より
(8) よって,定理 [#] より,最小多項式φ(x) は F[x] で既約である。
(終)
[3]
引き続き,準同型定理を利用していえること (上図) をまとめておくと,
(1) PIDの既約元は極大イデアルを生成するので,
⇒ (φ(x)) は F[x] の極大イデアルであるから,F[x]/(φ(x)) は体でもある。
⇒ これと同型な F[α] も体である [準同型定理]。
(2) 体として,F[α]=F(α) である [#] から F(α) の任意の元はαの多項式で表すことができる。
(3) そこで,β=f(α) となる多項式 f(x) を考えて,それを最小多項式φ(x) で割って,
f(x)=q(x)φ(x)+r(x) ( r(x) の次数は n より小さい。)
と変形すれば,β=r(α) としてよいことが分かります。つまり,F(α) の任意の元は,
β=c0+c1α+c2α2+・・・+cn-1αn-1
と係数 cj∈F を用いたαの (n−1) 次式で書ける,ということです。
(4) そして,F の拡大体 F(α) を F上のベクトル空間とみなしたときの基底は,
1,α,α2,・・・,αn-1
であり,拡大次数は n です。
[5] 以上のことは定理として述べておきましょう。
|
定理 β=g(α) と表すことができる。 |
この定理における g(α) を具体的に求める方法を示しておきます。
(1) 拡大体 F(α) の任意の元βはαと F の任意の元との間で四則演算を繰り返して得られるので,
P(x),Q(x) ∈ F[x],ただし,Q(α)≠0 を用いて,
β=P(α)/Q(α)
と書くことができます。
(2) そのとき,最小多項式 φ(x) ( 既約 ) と Q(x) は,(φ(α)=0 だが,Q(α)≠0なので ) F[x] 上で互いに素であるから,適当な 多項式 A(x),B(x) ∈ F[x] が存在して,
A(x)φ(x)+B(x)Q(x)=1
とすることができます。
(3) ここで,x=αとすると,B(α)Q(α)=1 であるが,この B(α) を用いれば,
β=P(α)B(α) ∈ F[x]
と表される。 (終)
|
定理 [ F(α):F ] = n = deg (φ(x) ) |
証明 (先の考察の繰り返しです。)
(1) F(α) の任意の元βを g(α),g(x) ∈ F[x] と表し,g(x) をαの最小多項式φ(x) で割って,
g(x)=φ(x)p(x)+r(x) ただし,deg(r(x)) < n
と書くことができる。
(2) ここで,x=αとすると,
β=g(α)=r(α)
つまり,g(x) の次数はφの次数 n より小さく,F(α) の任意の元βは F の元 ci を用いて,
β=c0+c1α+c2α2+・・・+cn-1αn-1
と表すことができ,F上のベクトル空間 F(α) の次元は,n 以下である。
(3) さらに,この次元が n−1 以下でないことを背理法で示そう。
もし,すべてが 0 でない ci ∈F が存在して,
c0+c1α++c2α2+・・・+cn-1αn-1= 0 ・・・・ [*]
を満たしたとすると,αを x と書き換えた次の F 上の (n−1)次多項式
f(x)=c0+c1x++c2x2+・・・+cn-1xn-1
はαを根にもつことになることを[*]は示している。これはφ(x) が最小多項式であることと矛盾する。
(4) したがって,[*] は成立せず,1,α,α2,・・・αn-1,は1次独立である。よって,
[ F(α):F ] = n
が成り立つ。 (終)
|
定義 F上で代数的な元α∈ F(α) の F 上の最小多項式 =0 の根をαと共役根という。 |
| 定理 体 F上の既約多項式φ(x)の根の1つをα1とすると,拡大体 F(α1) は剰余環 F[x]/(φ(x)) に同型であり,φ(x)のα1と共役な他の根をα2,・・・,αm とすれば, F(α1)= F(α2)=・・・=F(αm) ≡ F[x]/(φ(x))である。 |
証明 この定理もここまでの説明から明白ですが,念のため説明して置きましょう。
(1) φ(x) は F[x] の既約多項式であり,(φ(x)) は F[x] の極大イデアルなので,
(1) 剰余環 F[x]/(φ(x)) は体である。
(2) ここで,自然な準同型写像
Ψ: F[x] → F[x]/(φ(x))
と同型な写像として,
φ(x) → 0
x → α1 (既約多項式の根の一つ)
c → c ( c∈F )
を満たす中への写像を考えると,
F ⊂ F[x]/(φ(x))
である。そこで,この体 F[x]/(φ(x)) を F の拡大 F(α1) とみなせばよい。
(3) さらに既約多項式のα1と異なる共役な根α2,α3,・・・ であっても,Ψとして同様な準同型写像 (ただし,x → α2,もしくはx→α2・・・とする) を考えると,
同一の体,F[x]/(φ(x)) への準同型写像を導くことができるので,F(α1)= F(α2)=・・・=F(αm)≡F[x]/(φ(x)) である。
|
定義 F上で代数的な元α∈L の F 上の最小多項式が重根をもたないとき,αをF上で分離的という。特に全ての元α∈L について,F上で分離的であるとき,L は F 上で分離的,もしくは,L は F の分離拡大(体) であるといいます。 |
直感的には当たり前のように見える定義なので,「分離的でない例」 をあげておきます。
Fp(t) (p:素数) を有理関数体 [#] とすると,変数を t→tp とした Fp(tp) は,
Fp(tp) ⊂ Fp(t)
なので,体の拡大 Fp(t)/Fp(tp) を考えることができます。
このとき,体 Fp(tp)上では t の最小多項式は,
xp−tp (xp=tp のとき 0 となる。)
です。
ところが,その拡大体 Fp(t) 上では,
xp−tp=(x−t)p (x=t のとき 0 となる。)
のように因数分解でき,p 重根をもちます。よって,Fp(t)/Fp(tp) は分離拡大ではありません。
[2]
|
定理 |
証明
αの最小多項式が重根をもたないことを示せばよい。
最小多項式 φ(x) を n次多項式とすると,その微分φ’(x) は n−1次多項式となるが,標数 0 の体上では,これが恒等的に 0 となることはない。
そこで,φ(x)がαで重根をもつと仮定すると,φ’(α)=0 でなければならないが,これはφ(x)
が最小多項式であることと矛盾する。 証明終
ガロアの理論だけに興味がある方は,8 ガロア拡大とガロア群 へジャンプしても結構です。