| 14 溶液論へ(1)希薄溶液 | ||
| f-denshi.com [目次へ] 更新日: 09/08/30 | ||
| サイト検索 | ||
「 化学熱力学入門 」 における最後のテーマとなります。2成分2相系の特別な場合として, x1 >> x2,または一つの相においてx2=0 の場合について考察し,”溶液の熱力学” への序(本講義にとっては結びです)としたいと思います。
アルコールと水の混合系は気相でも液相でも任意の組成比をとることができます(もちろん相図には従いますが)。しかし,砂糖と水からなる系を考えると,液相(=砂糖水)には水と砂糖の両方が存在しますが,気相には水(水蒸気)だけが存在し,砂糖は全く存在しない状況があります。また,任意の組成比の水溶液も作ることもできません。このような現実によくある系のごく基本的な性質について考えてみましょう。
[1] 最初に希薄溶液の化学ポテンシャルを書き表す方法を紹介します。溶媒と呼ばれる成分1,n1mol と溶質と呼ばれる成分2,n2 mol から成り立つ溶液を考えます。希薄溶液とは,n1>>n2 である溶液を指して呼ぶことにします。 (x2=n2/(n1+n2)≒ n2/n1 とおけば,x2<<1 と条件をおくことができます。) ここで,念のために注意しておくと,「希薄」という言葉の意味が気体と液体とで違っています。気体の場合,希薄とは全体の圧力 P が低い,全体の密度が低いという意味で使いますが,希薄溶液の場合の希薄とは組成比が極端に偏っている,あるいは溶質の濃度が低いという意味で使っています。)
(化学で溶質とは,溶媒に溶けていない状態ならば,その圧力・温度で液体でない,つまり,気体や固体状態である物質が液体に溶けているときにそれを指して使う用語です。しかし,熱力学的には,溶媒に他の液体が溶けているときも同様な扱いができるので,そのような場合も含めてここでは溶質と呼んでいます。正確には混合溶媒の少ない方の成分というべきでしょうが。)
[4] 希薄溶液の自由エネルギー ( G = H−TS )は,
| 希薄溶液のギブス自由エネルギー : 成分1を溶媒,成分2を溶質とする希薄溶液のギブス自由エネルギーを, G=n1μ1+n2μ2 ・・・・・ (1)と各成分の化学ポテンシャルを用いて書くとき,その化学ポテンシャルは, μ1(T,P,x1,x2)=μ10(T,P,1,0)+RTlog x1 (溶媒の化学ポテンシャル) ・・・ (2) |
[5] ここで,(1)はどんな2成分系においても成り立つ一般的な関係ですが,(2),(3)は希薄溶液に対してだけ使われる関係式で,希薄な混合気体の場合と似ていますが,同じではありません。希薄な混合気体 (≒理想混合気体) に対する各成分のμj0 は任意の組成において純粋物質 j の化学ポテンシャルとすることができました[#]が,希薄溶液に対するμj0として,”純粋物質の化学ポテンシャル”を適用できるのは溶媒 (j=1,) に対してだけです。しかも,組成が,log x1≒0 と近似できる場合に限ります。したがって,溶媒の実質的な化学ポテンシャルを溶媒が純粋であるときの化学ポテンシャルだけを用いて,
μ1=μ10(T,P,1,0) 一定 ・・・・・ (2)’
として扱うことも多くあります。しかし,溶媒が主役となるような状況での議論では(2)を用いることとなります。
一方,(3)についてですが,希薄溶液の溶質の化学ポテンシャルμ2は,x2≒0 の状況の下で考えることになりますが,数学的に,x2→0 としてしまうと(3)式の第2項は−∞に発散してしまい,どんな定数μ20(T,P,1,0)を定めても有限なμ2を得ることができません。しかし,実在の系では希薄な極限において,μ20(T,P,1,0)はある定数で与えられると考えられます。なぜならば,希薄であることの物理的な意味を溶質について考えれば,ある濃度を超えて希薄になれば,(希薄気体の任意の気体分子どおしがそうであるように,)溶質分子間に相互作用が働かないほど離れ離れの状態となり,系全体の内部エネルギーの内訳として溶質どおしの相互作用は無視できる状態となるはずです。そのような状態下では溶質に割り当てられるモルエンタルピーは組成依存性をもたず,一定です。すると,そのような希薄濃度領域にある溶液の化学ポテンシャルの組成依存性は,理想気体の場合と同様に混合エントロピーに由来する第2項のRTlog x2 だけで与えられると考えられます。したがって,理想気体の化学ポテンシャルを導出したときと同様に考えて,希薄溶液の溶質の化学ポテンシャルを,
μ2(T,P,x2)=μ0(T,P)+RTlog x2
という形で書くことは妥当なことでしょう。ただし,μ0(T,P) はx2によらない定数で,先程述べたような意味で十分希薄な,あるモル分率 x0<<1 において溶質の正しい化学ポテンシャルが式,
μ2(T,P,x0)=μ0(T,P)+RTlog x0
で与えられるように定められるものです。したがって,溶質の化学ポテンシャルはこの基準点を採用して,
μ2(T,P,x2)−μ2(T,P,x0)=RTlog x2/x0
と書くことができます。しかしながら,x0を具体的に示すことは困難なので,これを,
μ2(T,P,x2)={μ2(T,P,x0)−RTlog x0}+RTlog x2
と書き直して,{ }を溶質のモル分率x2に依存しない定数,μ20(T,P,1,0) としてまとめ,溶質の標準化学ポテンシャルと呼ぶことにすれば,溶質の化学ポテンシャルは,結局,(3)で表されます。
[6] 当然ながら,この式が成立するのは,0<x2<<1のときだけで, x2が大きくなり,溶質どおしの相互作用を無視できない濃度になってゆくとμ20(T,P,1,0) の項もモル分率に依存して変化する可能性がでてきます。つまり,(3)式で溶質の化学ポテンシャルを記述することが困難になり,ほとんどの場合そうなります。 希薄な混合気体の場合,どんな組成の混合気体についても理想気体としてとり扱うことが可能 (つまり,任意のj,xj に対して,μj=μj0(T,P,)+RTlog xj と書いてよい) なのに対して,混合溶液ではどんな組成でもとはいかないのがふつうなのです。しかし,特殊な溶媒の組み合わせからなる混合溶媒においては,任意の組成において化学ポテンシャルを(3)のように表せる場合があります。このような液体を理想溶液といいます。(このとき,どちらが溶媒で溶質であるかの区別は意味がなくなります。)その場合, x2=1においても(3)がそのまま成り立つことから,
μ20(T,P,1,0)=μ20(T,P,0,1) =[純粋物質2の化学ポテンシャル]
すなわち,溶質の標準化学ポテンシャルも純粋な物質2の化学ポテンシャルを用いることができます。
[7] 系が2種類の混合溶媒からなる理想溶液であるとき,任意の組成における溶液の体積,エンタルピー,内部エネルギーについて,
理想溶液
体積 V=n1v10+n2v20
エンタルピー H=n1h10+n2h20
内部エネルギーー U=n1u10+n2u20
が成り立つことを示せます(演習)。ここで,vj0 は純粋な溶媒j のモル体積,hj0 は純粋な溶媒j のモルエンタルピー,uj0は純粋な溶媒のモル内部エネルギーです。
したがって,理想溶液の特徴として,
| ΔHmix≡ | nj(hj~−hj0)= 0 混合エンタルピー変化 (=混合熱) |
| ΔVmix≡ | nj(vj~−vj0)= 0 混合体積変化 |
という性質重要です。vj~はj 成分の部分モル体積,hj~はj 成分の部分モルエンタルピー。
この理想溶液についてはラウールの法則が重要です。
⇒ [#] 「各成分の蒸気の分圧はその溶液中のモル分率に比例する。」
[8] 理想溶液の具体例としてはベンゼンとトルエンとの混合溶媒が知られていますが,理想溶液とみなせる混合溶媒は極めて稀で,数学的な溶液モデルとしてだけ価値があるといえるくらいの位置づけです。本講義でも究極の2相2成分系の相図の理論式を導き出すために理想溶液を仮定しました[#]。
その一方で溶媒の混合に際して,発熱や吸熱が見られるが,エントロピー的な挙動は理想溶液とほぼ同じである混合溶媒系は比較的多くあります。このような性質をもつ溶液を正則溶液といい,溶液論の重要な分野の一つでした。
理想溶液の部分モルエントロピーが,
s~j=− ∂μj =sj0+R log xj ∂T P,x
であることを用いて,正則溶液のj番目の成分の化学ポテンシャルは,
μj=hj~−Ts~j=hj~−T(sj0+R log xj)
=μj0(T,P)+(hj~−hj0)+RTlog xj [正則溶液の化学ポテンシャル]
と定義することができます。hj~ はj 成分の部分モルエンタルピー,hj0 は純粋な成分j のモルエンタルピーです。
ΔHmix= nj(hj~−hj0)
によって正則溶液の混合熱が与えられます。さらに,
∂v~j = ∂vj0 ∂T P,x ∂T P,x
という関係を示すこともできます。(演習問題)
[9] もう一つついでに述べておくと,エンタルピー的な挙動だけでなく,エントロピー的な挙動も理想からはずれてくると,それは実在溶液と呼ばれて,
μj=μj0(T,P)+RTlog f xj
という見た目は簡単な式で記述されます。ここに登場するf は活量係数と呼ばれるもので,理想からのずれはすべてコイツのせいにしてしまいます。正則溶液であるならば,RTlog
f =(hj~−hj0)です。混合の際の理想からのずれは,分子の形や電気双極子の大きさなど分子の個性に基づいてはじめて定量的理解が可能です。
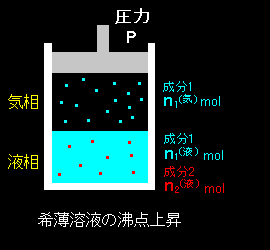 [1] 溶質が液相だけにしか存在できない場合,気液共存状態の条件式は,「溶媒(=成分1)の化学ポテンシャルが両相で等しい」として[#], ( x1 = 1−x2 )
[1] 溶質が液相だけにしか存在できない場合,気液共存状態の条件式は,「溶媒(=成分1)の化学ポテンシャルが両相で等しい」として[#], ( x1 = 1−x2 )
μ10(気)(T,P)=μ10(液)(T,P,1,0)+RTlog ( 1−x2 )
この式は,x2<<1 より, log (1−x2)≒−x2 として,
−x2≒ μ10(気)(T,P) − μ10(液)(T,P,1,0) RT RT
さらに,右辺を温度 T(=T0+ΔT) の関数 (P=一定) とみて,純粋な溶媒の沸点T0 の周りで展開すると,
| −x2≒ | μ10(気)(T0+ΔT,P) | − | μ10(液)(T0+ΔT,P,1,0) |
| R(T0+ΔT) | R(T0+ΔT) |
| ≒ | μ10(気)(T0,P) | + | ∂ | μ10(気)(T,P) | ΔT − | μ10(液)(T0,P,1,0) | + | ∂ | μ10(液)(T,P,1,0) | ΔT | ||||||||
| RT0 | ∂T | RT | T=T0 | RT0 | ∂T | RT | T=T0 |
↓0次の項はキャンセルされ,ギブス・ヘルムホルツの関係式 [#] を用いて,
| =− | h10(気)(T0,P) | − | h10(液)(T0,P,1,0) | ΔT | ||
| RT02 | RT02 |
| =− | L1 | ・ | ΔT |
| RT02 |
[2] ここで,L1=h10(気)−h10(液) は純溶媒が液体から気体へ変化する際のエンタルピー変化,すなわち気化熱です[#]。 得られた式を ΔT について解き,記号を L1 → Lb と改めれば,
沸点上昇温度
|
常に気化熱は,Lb>0 なのでΔTも正の値となります。したがって,一定圧力のもとで,
「希薄溶液の沸点は溶質濃度(モル分率)に比例して上昇する。」
ことがいえます。これは沸点上昇と呼ばれる現象です。
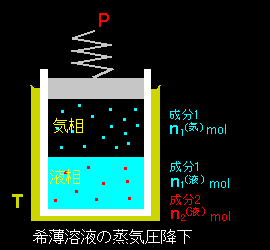 [3] 今度は温度一定の下での圧力依存性を調べます。溶質が液相だけにしか存在しない系の気液共存状態の条件式は先程と同じで,
[3] 今度は温度一定の下での圧力依存性を調べます。溶質が液相だけにしか存在しない系の気液共存状態の条件式は先程と同じで,
μ10(気)(T,P)=μ10(液)(T,P,1,0)+RTlog (1−x2)
⇔
−x2= μ10(気)(T,P) − μ10(液)(T,P,1,0) RT RT
となりますが,ここでは,これを P(=P0+ΔP ) の関数とみて,純粋な溶媒の蒸気圧 P0 の周りで展開します。
| −x2= | μ10(気)(T,P0+ΔP) | − | μ10(液)(T,P0+ΔP,1,0) |
| RT | RT |
| ≒ | ∂ | μ10(気)(T,P) | ΔP− | ∂ | μ10(液)(T,P,1,0 ) | ΔP | ||||||
| ∂P | RT | P=P0 | ∂P | RT | P=P0 |
↓ 熱力学関数の公式(12)[#]を使って, ちらも参考⇒[#]
= v10(気)(T,P0) − v10(液)(T,P0,1,0) ΔP RT RT
ここで,v10(気)(T,P0),v10(液)(T,P0,1,0)は純溶媒の気相,液相の平均モル体積です。これをΔP について解けば,
蒸気圧の降下
|
分母は,純粋な気体と液体 1 mol の温度 T,圧力 P0 における体積の差です。ふつう,液体より気体の方がずっと体積は大きいので,上式の分母は正,つまり,ΔP は負です。したがって,ある温度において,
「溶媒の蒸気圧は溶液中の溶質濃度に比例して降下する。」
ことがわかります。さらに,v10(液)(T,P0,1,0)=0 と近似すれば,
RT ≒p0 [純溶媒の蒸気圧] v10(気)(T,P0)
したがって,
ΔP ≒−x2p0
を得ます。これをファント・ホッフの法則といいます。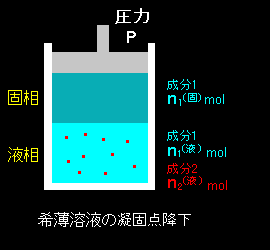
[1] 今度は液相と固相の2相共存状態を考えますが,溶質が液相にしか存在できないこととします。これは2.で希薄溶液の沸点上昇温度を求めたとき[#]と全く同じ考察(←気相を固相に置き換えただけ)によって次式が得られます。
ΔT= RT02 ・ x2 L1’
ただし,L1’=h10(固)−h10(液) は純溶媒が液体から固体へ変化する際のエンタルピー変化(=凝固熱)で,大抵の物質では負の値(発熱変化)をとります。つまり,ΔT<0 であり,凝固点は下がります。これを凝固点降下 といいます。
なお,多くの教科書では,系を昇温させる時の変化の方向を基準にした融解熱,Lm=−L1’ > 0 を用います。すると,
凝固点降下温度
|
用語の方も物質の融点降下と言い直すべきでしょうが,あまりこうは言いません。
沸点上昇,凝固点降下,ともに溶媒にだけ溶質が存在し,液相の化学ポテンシャルが純溶媒に比べて低下することによって引き起こされる現象であることを下図を見て納得してください。
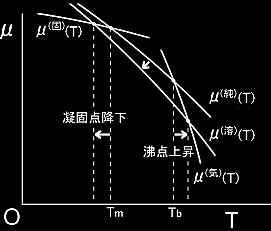 |
μ(固)(T):純溶媒の固相の化学ポテンシャルの温度依存性 μ(気)(T):純溶媒の気相の化学ポテンシャルの温度依存性 μ(純)(T):純溶媒の液相の化学ポテンシャルの温度依存性 μ(溶)(T):溶液の液相の化学ポテンシャルの温度依存性 |
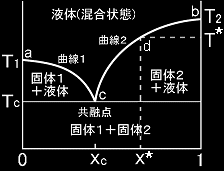 [1] 固体状態ではお互いまったく混じり合わないが,液体状態で十分温度が高ければ任意の組成で自由に混ざり合うような2成分系を考えます。そのような系の相図は一般的に右図のようになります。成分1の融点をT1,成分2の融点をT2とし,T1<T2であるとしましょう。横軸は各相の成分2のモル分率です。
[1] 固体状態ではお互いまったく混じり合わないが,液体状態で十分温度が高ければ任意の組成で自由に混ざり合うような2成分系を考えます。そのような系の相図は一般的に右図のようになります。成分1の融点をT1,成分2の融点をT2とし,T1<T2であるとしましょう。横軸は各相の成分2のモル分率です。
温度がT2より高ければ,どんな組成,xにおいてもこの2つの物質は均一に混じり合います。ところが温度を下げていくと,例えば,xc<x*<1であれば,温度T*において,曲線2とぶつかることになります。すると,その点dにおいて純粋な成分2の結晶が析出を始めます。この固体結晶には成分1は全く含まれていません。さらに温度を下げていくと,純粋な成分2の結晶は徐々に増加していきますが,液体からは成分2が失われるために曲線2に沿って液体の組成が変化していきます。この曲線は,液体と固体2との2相共存条件を表しているのです。そして温度がTcまで下がると,そこでは成分2だけでなく,成分1も固体が安定であり,成分1と成分2の混じった混晶がcの点で析出します。
系の組成が,0<x*<xc であるときは,上の説明における成分1と2との役割を交代した現象が起きます。特に,x*=xcであれば,液体を高温から冷却していくと,温度がTcに達したときのみ固体(混晶)への転移が起きます。逆に温度を上げていけば,この温度Tcにおいてのみ融解が見られます。この点では,液体と成分1からなる固体と成分2からなる固体の3つの相が共存する状態であり,自由度は1です。圧力を指定すれば,残りの自由度はゼロであり,Tcの温度,組成は唯一定まります。この点cをこの2成分系の共融点(eutectic point),または共晶点と呼びます。
[2] 曲線1,および,曲線2を表す理論曲線を求めてみましょう。そのために,水ーアルコールの液体と蒸気を念頭においた考察で導いた2成分2相共存平衡条件を与える微分方程式[#]において,Y相を気相ではなく,固相とみなしましょう。すると,液相であるX相の組成は,成分2のモル分率をx2として,
∂T = (x2−y2) RT2 ・・・ [**] ∂x2 P x2(1−x2){(1−y2)L~1+y2L~2}
を満足しなければなりません。ここで,L~1=h~1(固)−h~1(液),L~2=h~2(固)−h~2(液)は,それぞれの成分が液体から固体へ変化するときのエンタルピーー変化で,この相転移は発熱反応なのでL~1,L~2 ともに負の値をとります。 また,固相の組成を表す y2 (=固相の成分2のモル分率) ですが,今考えている系では,どんな値でも取れるわけではなく,曲線2上では,成分2しか固相に存在しないので,y2=1でなければいけません。すなわち上の式[**]は,
∂T =− RT2 ∂x2 P x2L~2
となります。これを,温度T2から,T,組成1から,x2まで積分すれば,
log x2 = L~2 1 − 1 R T T2
これをTについて書き直せば,
T= T2 [曲線2] 1+(RT2/L~2) log x2
となります。これが,曲線2を与える理論式です。
[3] 同様に,曲線1についても,y2=0 の下で微分方程式[**]を解けば,
log (1-x2 )= L~1 1 − 1 R T T1
T= T1 [曲線1] 1+(RT1/L~1) log (1-x2)
となります。これを点 a の近く,すなわち,x2<<1として,log (1-x2)≒-x2,T=T1+ΔTと近似すると,
-x2 = L~1 1 − 1 ≒ L~1 -ΔT R T1+ΔT T1 R T12
ΔT≒ RT12 ・ x2 L~1
これは先程求めた凝固点降下の式に他なりません。
なお,蛇足ですが,曲線1と曲線2を T,および,x2の関数とみて,連立して解けば,共融点を与える温度 T=Tc と組成 x2=xc を求めることができます。
難溶性のイオン化合物が溶媒にごくわずかだけ解離しながら溶けて飽和している(=平衡状態にある)とします。それを化学反応式で,
AmBn →
←mAn++nBm- 固体 溶液中
と表わしてよい場合を考えます。ここでは固相の熱力学状態は溶解・析出反応の進行具合によらず一定なので,その化学ポテンシャルは,
μAB=μAB0(T,P) (固相AmBnの化学ポテンシャル)
と書くことができます。固相中の化学種はAmBnだけなので,その固相のモル分率 xAB(固) は常に1なので,第2項にあるべき,RTlog xAB(固) =0 を省略したと考えてもよいでしょう。一方,液相の溶媒,陽イオンAn+,陰イオンBm-のモル分率を x1,xA,xB とすると,それらの化学ポテンシャルは,
μ1=μ10(T,P,x1=1)+RTlog x1 (溶媒の化学ポテンシャル)
μA=μA0(T,P,xA≒0)+RTlog xA (溶質An+の化学ポテンシャル)
μB=μB0(T,P,xB≒0)+RTlog xB (溶質Bm-の化学ポテンシャル)
となります。(正しくは各変数の右肩に(液)という記号をつけるべきなのですが,今の場合,煩雑になるだけなので省略しています。)ここで希薄溶液を考えているので,μ10(T,P,x1=1)は純溶媒の化学ポテンシャル,μA0(T,P,xA≒0)は溶媒中に極微量のAn+が溶媒中に存在する領域で,μAとRTlog xAとを直線関係で近似したときのy切片となります。μB0(T,P,xB≒0)もBm-に対する同様な量となります。また,x1=1−xA−xB≒1と近似すると,溶媒の化学ポテンシャルの第2項は≒0となり,μ1=μ10 ,すなわち,xA,xB とは無関係な定数です。
次に溶質の化学ポテンシャルをモル濃度[mol/dm3]を用いて書き直しましょう。溶媒,陽イオンAn+と陰イオンBm-の濃度をそれぞれC1,CA,CBとします。溶液が希薄であることから,
xA≒ CA ・ xB≒ CB C1 C1
とおくことができ,
μA≒μA0+RTlog CA C1
= μA0−RTlog C1 +RTlog CA C0 C0
=(μA0−RTlog C1)+RTlog CA
ここで,C0=1[mol/dm3]は基準濃度であって,対数の中身を無次元にするために導入しています。同様に
μB≒(μB0−RTlog C1)+RTlog CB
これらを用いて,平衡条件を書き下ろすと,
ΔG = νjμj
=m μA+n μB−μAB
={m(μA0−RTlog C1)+n(μB0−RTlog C1)−μAB0(T,P) } +mRTlog CA +RTlog CB
=0
さらに,{ } の部分をまとめて,
ΔG0(T,P) ≡ mμA0+nμB0−μAB0(T,P)−RTlog C1m+n
を定義して書き直すと,
ΔG =ΔG0 +RTlog CAmCBn = 0
したがって,平衡定数を,
K=exp (−ΔG0 /RT)
とすると,
CAmCBn=K
と書くことができます。この平衡定数 Kは溶液に飽和している陽イオンAn+と陰イオンBm-の濃度の積を与えるため溶解度積と呼ばれ,Ksp としばしば書きます。
以下は削除した部分
さて,ここでは温度,圧力を独立変数として話を進めますが,そのとき内部エネルギーについて成り立つ関係
,( T,P は状態変数なので,[#] )
U(T,P,n1,n2)=n1U(T,P,1,x) ・・・・・・・ [*]
をxの関数とみて,x=0 の周りにテーラー展開し,第1項までとれば,
ただし,各成分の化学ポテンシャルの意味は,
|
||||||||||||||||||||||||||
|
上の導出では, [*] の両辺を n2 で偏微分して,
であることを使ってます。 (n2/n1≒x) |
[2] 同様に,体積についても
|
V( T,P,n1,n2 ) ≒ n1v1+n2v2 ただし,
|
||||||||||||||||
[3] したがって,組成一定の下では,dU = n1du1+n2du2, dV = n1dv1+n2dv2 であることに注意すれば,希薄溶液のエントロピーの微分量は,
dS= dU+PdV =n1 ・ du1+Pdv1 +n2 ・ du2+Pdv2 T T T
=n1ds1+n2ds2 ( s1 は純粋な物質1の部分モルエントロピーです。s2 はちょっとイミは複雑(^〜^))
と表せます。これを積分して,
S=n1s1+n2s2+C(n1,n2) ・・・・・ (2)
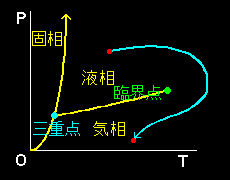 となります。 積分定数:C(n1,n2) は,TやPには無関係です。 注意してほしいのはここまで,対象を混合溶液として議論してきたつもりなのですが,ここまでの式の導出に液体であることを特徴づけたり,話を液体に限定するような要請はありませんでした。実際に臨界点を迂回する右のような経路をたどって,圧力・温度を変化させれば,相転移を経ることなく液体状態は気体状態に連続的に変化します。つまり,今,導いた式(2)は,この系が気体であるときにも成り立つものです。
となります。 積分定数:C(n1,n2) は,TやPには無関係です。 注意してほしいのはここまで,対象を混合溶液として議論してきたつもりなのですが,ここまでの式の導出に液体であることを特徴づけたり,話を液体に限定するような要請はありませんでした。実際に臨界点を迂回する右のような経路をたどって,圧力・温度を変化させれば,相転移を経ることなく液体状態は気体状態に連続的に変化します。つまり,今,導いた式(2)は,この系が気体であるときにも成り立つものです。
そこで,(2)式と以前導いた気体の混合気体のエントロピー[#]:
S=n1s10+n2s20−R(n1 log x1+n2log x2) とを比較して,
C(n1,n2)=−R(n1 log x1+n2log x2)
と定めることができます。すなわち,希薄溶液のエントロピーは,
S=n1s1+n2s2−R(n1log x1+n2log x2)
ただし,x1=n1/(n1+n2),x2=n2/(n1+n2) となり,混合気体[#]と同様な形式で表されます。