12　混合エントロピー
f-denshi.com  [目次へ]　更新日： 08/07/06

１．混合エントロピー　

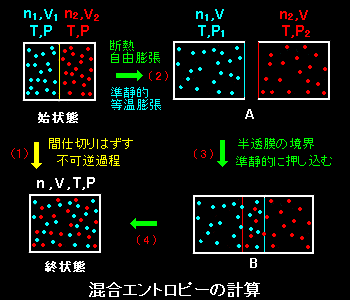
[１]　２種類の理想気体とみなせる n1モルの気体１と n2モルの気体２が，間仕切りで体積が V1，V2 に分離された断熱容器の中にそれぞれ左右分かれて閉じ込められており，同じ温度T，圧力P にあるとします(始状態)。ここで，

(1)　間仕切りを取り除くと，２種類の理想気体は均一に混じりあい，平衡状態に達する(終状態)。このときの温度，圧力は，T，Pのままで，粒子数はn＝n1＋n2，体積はV＝V1＋V2となる。

この現象はもちろん不可逆過程ですが，系は外部と熱や仕事の交換をまったくせず，エントロピー変化だけが起こります。断熱容器の中で理想気体とみなせる２種類の気体を混合する時のエントロピー変化を混合エントロピーといいます。

[２]　この過程は不可逆過程なのでエントロピーを直接計算できません。計算を可能にするためには，始状態と終状態とを結びつける準静的な過程を見つける必要があります [#] が，そこで考え出されたのが半透膜を使う次のような２種類の気体の混合方法(思考実験)です。まず，

(2) 断熱自由膨張によってそれぞれの気体の体積をともに，V1＋V2 にする。

この過程そのものは不可逆ですが，後ほど述べるように同じ状態変化を与える可逆的な等温膨張過程に置き換えることが可能です。ここで，この容積がV1+V2である断熱容器は半透膜でできており，

　　　　気体１を閉じ込めている容器は気体１は全く通さないが気体２は自由に通す。
　　　　気体２を閉じ込めている容器は気体２は全く通さないが気体１は自由に通す。

という性質を持っているとします。次に，

(3)半透膜の容器を互いに入れ子の状態に押し込んでゆくと，容器の重なった部分には両方の気体が入ります。
(4)重なりが完全になるまでゆっくり押し込むと，体積 V1＋V2 の中で２種類の気体も完全に混合されます。(終状態)

このような半透膜を利用した気体の混合過程をすべて準静的な過程とみなせば，エントロピーの計算が可能です。

[３]　それでは計算です。

(2)の断熱(自由)膨張過程は不可逆過程なので，そのまま熱の出入りが0であることを用いてエントロピーの計算をすることはできません[#]。（つまり，エントロピー変化が0とするのは間違い！教科書にはふつう正しいことだけが記述されがちだが，間違いを示して，それがなぜ間違いかを理解することも重要。)　しかし，理想気体はこの過程で温度変化がないので，これを可逆的な等温膨張過程に置き換えて，エントロピー変化を計算することができます。「不可逆過程のエントロピー変化の計算　⇒　その過程と同一の始状態，終状態をもつ可逆変化を探せ！」ということです。

熱力学第一法則 [#] においてdU＝0とすると，TdS＝PdV。これに理想気体の状態方程式を用いて，

dS＝ PdV ＝ nR dV
T V

この関係式より，準静的等温膨張による気体１のエントロピー変化は，

ΔS1＝ V1＋V2 n1R dV ＝n1R log V1＋V2 ≒n1R log n1＋n2 ＝−n1R log x1
V1 V V1 n1

と計算できます。ここで，≒のところでドルトンの分圧の法則[#]を用いています。同様に，

ΔS2＝−n2R log x2

となります。半透膜を押し込む準静的断熱過程(各々の気体についてみると何事も起こっていない！)ではエントロピー変化は 0 なので，結局，いま計算したΔS1とΔS2の和が始状態と終状態とのエントロピー差になります。すなわち，

ΔSmix＝ΔS1＋ΔS2
　　　　＝−R(n1 log x1＋n2log x2)　　[混合エントロピー]

となります。ここで，x1,x2＜1 であることから，必ず，ΔSmix＞0 であることにも注意しましょう。

これに関する「ギブスのパラドックス」について欄外に説明があります。⇒[ギブスのパラドックス]

[４]　これより混合気体のエントロピーは純粋な気体１，２ のモルエントロピーをそれぞれ，s10，s20 として [ 注意 ] ，

S＝n1s10＋n2s20−R( n1 log x1＋n2log x2)

　＝n1{s10−Rlog x1}＋n2{s20−Rlog x2}

と書くことができます。混合後のエンタルピーについては，純粋な気体１，２ の１モルあたりの量をそれぞれ h10，h20　とすれば，

H＝n1h10＋n2h20

と単純な和で表せるので，結局，気体１，２ の混合系について， ギブスの自由エネルギー　G ＝H−TS　は，

G＝n1h10＋n2h20−T[ n1{s10−Rlog x1}＋n2{s20−Rlog x2} ]
  ＝n1{ h10−Ts10＋RTlog x1 } ＋ n2{ h20−Ts20＋RTlog x2 }

と書いてよいでしょう。これをまとめると，

混合気体のギブス自由エネルギーと化学ポテンシャル

G＝n1μ1＋n2μ2　
　＝n1{μ10＋RTlog x1}＋n2{μ20＋RTlog x2}
ただし，μj0＝hj0−Tsj0　　 [純粋な j 成分気体1mol のギブス自由エネルギー]。　
と書き表すことができる。また，　
　μj＝μj0＋RTlog xj　　　
を　混合気体の成分 j の化学ポテンシャル　という。　　　( j ＝ 1,2 )

この議論は成分がm個に増えてもそのまま拡張できるのは説明するまでもないでしょう。

G ＝  njμj     ； μj＝μj0＋RTlog xj　　，xj＝nj /(n1＋･･･＋nm)

　理想気体とみなせる気体どおしの混合系では，成分気体の一つ一つの化学ポテンシャルがその成分の純粋状態の化学ポテンシャルとその成分の組成比だけによって表されるのです。このように各成分ごとに具体的に化学ポテンシャルを書き下すことで，多成分系の熱力学的取り扱いを相対的な比較から絶対的な定量的取り扱いへの足がかりを作ることができました。

補足

化学ポテンシャルが，

μ＝μ0＋RTlog P
P0

で与えられることを通して混合エントロピーを求める方法もありますが，それは別の機会で。

[ 注意 ]

　　前章まではもっぱら２つの状態間の ”エントロピーの差：dS” を問題にしてきましたが，この章では，”絶対モルエントロピー： s0 ” という概念を導入しています。これはいわば，静電気学における，”電圧” と ”電位” の違いのようなものです。実験で直接，確かめられる量は２つの状態間の差(相対的な量)ですが，ふつうこれをそのまま記録，体系化するようなことはしません。基準値(原点)として，適当な状態を一つ選んで，他の状態はすべてこの基準値からの差として記録します。静電ポテンシャルの場合は無限遠を0としましたね。 エントロピーの場合，学術的には絶対零度に基準値を求めます。(熱力学第３法則参照)　





[目次へ]

CopyRight　フジエダ電子出版

［ギブスのパラドクックス］

複数の方々（学生さん）から同じような質問を度々頂いたこともあり，簡単な説明をここに書いておくことにしました。　(2008/9/24)

ギブスのパラドックスとは？

本文中では，それぞれ，n1，n2モルの２種類の気体を混合したときのエントロピー変化が，

（Ａ）　　ΔSmix＝−R(n1 log x1＋n2log x2)　＞　0　[混合エントロピー]

であることを示しました（記号の意味は本文中と同じ）。ところが，間仕切りの左右の気体１と気体２がもし同じ温度，圧力にある同種類の気体だとしたら，間仕切りを取り去っても巨視的には何も変化は起こりません。したがって，エントロピーも変化しないはずで，

（Ｂ）　　ΔSmix＝0

という主張ができるはずです。本文中での混合エントロピー（Ａ）を導出する際には，気体１，気体２の個性を示すような物理量は何も使ってないので，同一種類の気体の混合に対しても（Ａ）のような計算ができます。よって，２通りの結果が導かれるのは矛盾ではないかというのがギブスのパラドックスと呼ばれるものです。

まず，同一種類の気体の混合に対して，どちらの混合エントロピーが正しいかと言えば，（Ｂ）です。同一種類の気体の混合によるエントロピー変化はゼロです。それでは本文中の（Ａ）のような計算はナンセンスなのかと言えば，本文中の計算方法も２種類の異なる気体の混合に対しては，正しいエントロピー変化を与えています。したがってこれはこれで大学生の早い時期にきちんと勉強して理解しておく必要があります。特に化学への応用はこの概念なしでは1歩も前に進みません。

では，同一の粒子に対する（Ａ）の計算方法と（Ｂ）の計算？方法で何が違うのかと言えば，

（Ａ）　　左右にある同一種類の粒子を区別できるものとして扱っている。
（Ｂ）　　左右にある同一種類の粒子は区別できないものとして扱っている。

という違いがあります。つまり，（Ａ）においては，容器の間仕切りの左側にあった気体１も右側にあった気体２も，間仕切りを取り去った後には容器全体に広がるとして，エントロピー変化を計算していることになります。つまり，もともと粒子が左側にあったのか右側にあったかが識別可能として，混合によるエントロピー変化を計算していることになります。もし，左右で異なる気体が入っていたならば，たしかに混合後も気体粒子の一つ取り出したとき，それが元々，右側にあったか左側にあったか言い当てることができます。しかし，左右に同一の気体が入っていた場合はそれができず，（Ａ）の処方箋は無効となるのです。

一方，（Ｂ）の間仕切りを取り払った後に何も起きないという主張には，容器の中を動きまわる同一種類の粒子を一つ一つ区別することは不可能だということが暗に含まれています。この前提があるからこそ間仕切りをとっても何も起きないと主張できるわけです。もし，間仕切りを取り除いてしばらくしてからも，「はじめ右にあった粒子が左に移動しよった」というようなことがわかるのなら，それは，「間仕切りをとっても何も起きない」という主張とは相反します。つまり，（Ａ）と（Ｂ）とでの混合エントロピーの解釈の違いは同一種類の粒子の識別可能性の可否に基づいているのです。

熱力学では（統計力学でも），巨視的に区別ができない熱平衡状態を一つの同じ状態として扱う学問なので，今の場合，（Ｂ）の主張をとることになりますが，では間仕切りが取り除かれた瞬間に，突然，左右にある気体粒子は識別不可能となったのでしょうか？私の理解している限りでは，「間仕切りが存在している状態においても左右にある同一の粒子を区別することは原理的に不可能」とすることが古典統計力学の体系化がもっともスマートにいく方法ということでコンセンサスが得られているのではないでしょうか。

えっ? 間仕切りの左にあった分子は間仕切りがそのままなら，ずっと左にあるはずだって？　じゃあ，もし，あなたがよそ見をしている間に，悪魔のエフがやってきて，間仕切りの左右にある同一種類の気体粒子を，温度，圧力が変化しないようにこっそり，ごっそり同じ数だけ交換したとしたらあなたは気がつくでしょうか？　きっとあなたは全く気がつかずに，エフのやってくる前と同じ物理法則をその系にそのまま適用してしまうことでしょう。

実用的には同一種類の気体の混合エントロピーを計算する必要に迫られることなどまずないので，ここに書いてあることを知らなくてもなにも困ることはないのですが，･･･これはヒミツのハナシ。