化学ポテンシャル
分割した前半です。 多成分系の化学ポテンシャルは 10-2 にあります。
注意： 部分モル量を表す記号として， 「v~,s~,u~,g~,h~,f^」を用いています。
|
10-1 単一成分系の 化学ポテンシャル |
|
| f-denshi.com ［目次へ］ 更新日： 21/11/03 分割した前半です。 多成分系の化学ポテンシャルは 10-2 にあります。 |
||
| サイト検索 注意： 部分モル量を表す記号として， 「v~,s~,u~,g~,h~,f^」を用いています。 |
||
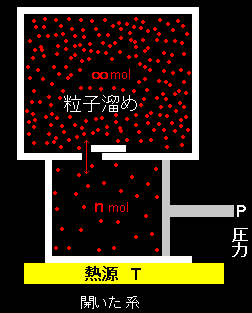［１］ いくつかの専門用語の説明からはじめます。系が熱，仕事だけでなく，質量(物質)も外界と交換する系を開放系といいます。その場合，系の内部エネルギーなども質量の増減とともに変化しますが，系の質量に依存する熱力学変数を示量変数といいました。一方，温度，圧力などは系の質量とは無関係に定まる変数で，示強変数といいました。
それから，部分モル量(partial molal quantity) と呼ばれる用語です。これは熱力学関数(変数)を示強変数 T,P 一定の下で，その系の粒子数（モル数）で偏微分した量で，その変数に ~ をつけて表すこととします。
具体的には，v~，s~，u~，g~，h~，f~ があります。
(一般的な教科書では変数の上に - (bar) をつけて表しますが，web上でこれを出力するのは煩雑なので ~ で代用します。 )
u~≡ ∂U ，g~≡ ∂G ，h~≡ ∂H ∂n T,P ∂n T,P ∂n T,P
f~≡ ∂F ，s~≡ ∂S ，v~≡ ∂V ∂n T,P ∂n T,P ∂n T,P
「部分」という用語は偏微分の偏 (partial) からきています。この化学ポテンシャルという概念は，多成分系に用いたときに真価を発揮するものなのですが，ここでは前ページの話のつづきということで，純粋な一種類の分子から構成される開放系 (不均一系) について考えることから始めます。
ギブス自由エネルギー： G(T,P) の独立変数 T，P はともに系の質量に依存しない示強変数ですが (←このことが熱力学関数の中で G が少し特別な地位を与えている！) ，G自身は示量変数 (〜示量関数) なので，その量は系の質量，つまり，モル数に依存し，n モルからなる系のギブス自由エネルギーを正確には，G(T,P,n) と書く必要があります。このとき，
G(T,P,n) ＝ nG(T,P,1) ･････ [*]
の関係が成立しています。数学では同次関数に関するオイラーの関係式[#]と呼ばれる式です。この式のn による偏微分は，
∂G(T,P,n ) ＝G(T,P,1) ･･･ [**] ∂n T,P
となりますが，この左辺，すなわち，G(T,P,n ) の部分モルギブス自由エネルギー g~(T,P) を系の化学ポテンシャルと定義し，
μ(T,P) ≡ ∂G(T,P,n ) ( ＝g~(T,P) であるがこの表記ではなく，μ(T,P)を使う。) ∂n T,P
と書くことにします。単位は [kJ/mol] がしばしば使われます。
くどいが重要な注意
上式から，１モル当たりのギブス自由エネルギー (＝(平均)モルギブス自由エネルギー) を g(T,P) と書くことにすれば，μ(T,P)＝G(T,P,1)≡g(T,P)が成り立ちますが，この左右だけを見て，化学ポテンシャルを，系の「１モルあたりのギブス自由エネルギーg(T,P)」と定義する，と端折るのは間違いです。もう一回よーく，定義を読み返してください。あくまで，G(T,P,n ) の n による偏微分が化学ポテンシャルです。
決して，μ≡g(T,P) ではありません。 そうやってしまうと，同次関数に関するオイラーの関係式[#]と呼ばれるこの関数G(T,P,n)を制限している重要な条件式[*]を見失うことになってしまいます。[**]は[*]が成り立って初めて成り立つ式なので，μ≡g(T,P)として＝を無視すると，＝も無視したことになります。
どうしてもここで，「１モル」という言葉を使いたければ，
「系の粒子数が等温，定圧下で変化する際の系のギブス自由エネルギー変化を粒子１モル当たりに換算した量を化学ポテンシャルと呼ぶ」としなければいけません。なお，多成分系の化学ポテンシャルと平均モル自由エネルギーとの正しい関係は後ほど説明します。⇒[#]
それから，[**]の物理的解釈ですが，タンクに純水が10キロリットルほど入れてある状況（＝系）を思い浮かべてください。そこへ同じ温度・圧力にある１モル(＝18g)の純水を加えると，この系のギブス自由エネルギー G はどれだけ変化しますか？
その答えは，「純水１モルがもっているギブス自由エネルギー G(T,P,1)＝g(T,P)である。」となります。[**]はこのような当たり前のことを式で表したものです。これも後ほど再考します。
ところが，タンクの中身が水の他にアルコールを含む２成分系の場合は違ってきます。系に水1モルを加えたからといって，そのまま，水１モルが持っているギブス自由エネルギーが系に加算されるわけではありません。もっとずっと慎重な議論が必要となります。
［２］ さて，変数 nが追加され，G(T,P,n)と書くと，G(T,P)と書く場合に比べて純物質の熱力学状態を定める自由度が２つから３つに増えたように思えますが，それは違います。数学的に説明すると，変数 n の追加に対して，条件式
G(T,P,n) ＝ nG(T,P,1)
も追加されているからです。また，変数μも追加されているように見えますが，μに対しては次の定義式，
μ(T,P) ≡ ∂G(T,P,n ) ∂n T,P
が追加されているので系の自由度が増えるわけではありません。追加された第１番目の式はオイラーの関係式で，第２番目の式は化学ポテンシャルの定義式です。この２式は数学的に独立した式です。また，この２式から，
μ(T,P) ≡ ∂G(T,P,n ) ＝G(T,P,1)＝ G(T,P,n) ∂n T,P n
が純粋物質に対して導かれます。すると， G＝nμ を n とμの関数とみなした全微分は，
(1) dG ＝ ndμ＋μdn
となります。一方，G(T,P,n)の全微分は，
(2) dG ＝ ∂G dT＋ ∂G dP＋ ∂G dn ∂T P,n ∂P T,n ∂n T,P
＝−SdT＋VdP＋μdn (← [#])
これら２式から導かれる条件式： (辺々引いて)
−SdT＋VdP−ndμ ＝ 0
をギブス-デュエムの式といいます。名前が付いているようにたいへん有用な関係式ですが，その使い方は後で紹介します。
もう一言，
ギブス-デュエムの式をnで割って，
dμ＝ − S dT＋ V dP ＝−sdT＋vdP， ただし，s＝S/n，v＝V/n n n
と n を見かけ上消去できます。ここで純物質に限っては，μは１モル当たりのギブス自由エネルギーG/nに等しいので，ギブス-デュエムの式とは，自由度が２であることを示している dG ＝−SdT＋VdP なる式を１モルの物質について書き表したものに過ぎないことがわかります。
なお，「nを明示しても純粋物質の熱力学的自由度は変わらない」ということの物理的な意味は，ある決まった温度，圧力のもとにある１モルの水と２モルの水とが異なる熱力学状態にあるとは考えないことと理解してもいいでしょう。コップ１杯の水と２杯の水とで，同じ大気圧下での沸点 (厳密には気液共存状態の条件) が異なったりはしないでしょう？
化学ポテンシャルとはこういった質量に直接依存しない現象を解明するため考え出された最強の武器なのです。状態方程式PV＝RTに従う気体の熱力学的な自由度は２つなのに対して，PV＝nRTに従うとするときは，n も変数にカウントして，気体には自由度が３つあると考えたりしないのも同じ理由。モル数 n というのは人間が適当に決めた単位数量に過ぎず，その決め方によって熱力学的自由度が変わったりはしないのです。熱力学状態の自由度に係わるこの種の量は組成を表す示強変数，モル分率であることが次ページでわかります。
話をもとに戻すと，ギブス自由エネルギーの場合，自然な変数を用いて，
G(T,P,n)＝nG(T,P,1)＝ng(T,P)＝nμ(T,P)
でしたが，他の熱力学変数の場合はこうはなりません。
例えば，ヘルムホルツ自由エネルギー（自然な変数はT,V）については，
F(T,V,n) ≠ nF(T,V,1) であり，正しくは F(T,V,n) ＝ nF(T,V/n,1)
となっています。
ということは，F(T,V,1) ＝f(T,V) のような定義にはあまりメリットが存在しません。同様に自然な変数で表した，エンタルピーH(S,P,1)，内部エネルギーU(S,V,1) に対してもギブス自由エネルギーに対して成り立つ[*]および，[**]の＝のような関係は成り立ちません。
G(T,P,n)に対して，このオイラーの関係式が成り立ち，G(T,P,n)＝nμ(T,P)と書ける理由は，Gの変化が独立変数として，圧力P，温度Tという示強変数の変化のみで記述が可能だからです。つまり，全微分で，
dG ＝−SdT＋VdP
と書けるということです。一方，F(T,V,n) は V が示量変数なので，F(T,V,n) ≠nF(T,V,1)なのです。
この様子は例のウガンダハイフン（右図）[#]を見れば一目瞭然ですね。それゆえ，G(T,P) の変化は直接質量に依存しない現象 (熱平衡状態) の記述に有用なのです。
| H | |||||
| S 示量変数 |
|
P 示強変数 |
|||
| U |  |
G | |||
| V 示量変数 |
|
T 示強変数 |
|||
| F |
ただし，G(T,P)そのものが示強性ということではありません。自由度が２とすぐわかるように，dG＝VdP−SdT と書いて，nを明示しないときであっても，系を構成する ｎ モルの物質のエントロピーや体積いう意味で，S や V に n が潜んでいるのです。つまり，係数，-S，V を通してG(T,P)そのものは示量性なのです。)
力学での例えだと，水に物体が浮くか沈むかが示強変数，密度によって評価できることと同じです。質量も体積も直接は関係ないのです。前ページで２相平衡条件を求めた際，平衡にある相の１モル当たりのギブス自由エネルギー (＝化学ポテンシャルでもある)が等しいという結果[#]がえられた理由はここにあります。１モルのヘルムヘルツ自由エネルギー F(T,V,1) を比較してもダメなんです。Ｆの自然な変数 V が示量変数のために熱平衡条件に直接関与できないのです。(熱平衡状態では，系全体について P，T が一定であることが必ず要請されるのです。)
以上が他の熱力学関数 F，H，U をさしおいて，熱力学関数 G が熱力学の中で特別な地位を獲得している理由です。
［３］ しかし，G(T,P,n) のルジャンドル変換と各熱力学変数の全微分を比較して，
|
の関係を確かめることができます。この等式はこれまで G(T,P,n) が F，H，U に比べて特別だと説明してきた経緯からはちょっと困った不思議な関係式です。
しかし，冷静に考えれば，U，G，H，F は変数変換によって互いに写り変われるのだから，当然のことです。
これ↑は化学ポテンシャルを説明しようとするとき，初学者に混乱を引き起こす原因になっていると思う。)
[***] を眺めるときの注意点として，熱力学関数を n で偏微分する際，一定にさせておく変数が熱力学関数ごとにそれぞれ異なることを指摘しておく必要があります。例えば，
μ＝ ∂F ≠ ∂F ≡f~ ∂n T,V ∂n T,P
であることなどに注意をはらってください。
特に重要な G と F の２つについて偏微分の物理的意味を確認すると，[***]式の左端のギブスの自由エネルギーは，温度，圧力が一定の下で粒子数を変化させると，それに伴って変化するのは体積とエントロピーとなります。一方，ヘルムホルツ自由エネルギー F では，温度，体積一定の下で粒子数を変化させると，それに伴い変化できるのは圧力とエントロピーなのです。
この２つの偏微分の物理的な意味を図に描いてみると次のようになります。(粒子の色の違いは意味がありません，念のため)
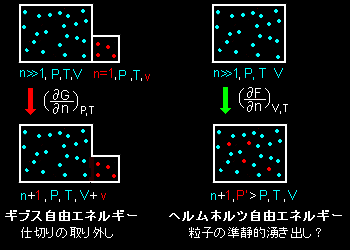
この図で分かるように粒子数が１モル増加したときのエネルギー増加をオイラーの関係式を満たしているギブス自由エネルギーでは，系と同質な１モル分の系(体積)の増加によって表現され，一方，ヘルムホルツ自由ネルギーの場合は系の体積を保ったまま，系と同じ温度で湧き出した粒子１モル分の圧力の増加で表現されることになります。すなわち，
ギブス自由エネルギーの増減は，仕切りの開閉
ヘルムホルツ自由エネルギーの増減は，粒子の準静的湧き出し･消滅
となります。変化するエネルギーの形態は両者でまったく違うのですが，その分量は同じだよということが，化学ポテンシャルの定義式，[***]で述べられているのです。
この違いは，
粒子の増減に際して T，P を変化させない G は，熱平衡状態を考える上でたいへん質のいい関数であり，一方，粒子の増減に際して P が変化してしまう F は，熱平衡状態を考える上で質の良くない関数となっている
ということの理由を説明しています。前ページで見たように，熱平衡にあるときは，すべての相の温度と圧力が同じであることが要請されるので，P，T 一定の下での粒子数の変化に注目することは熱平衡の記述を簡潔にすることができるのです。
（なお，上図やその説明に使われている準静的な粒子の湧き出しなどという用語はここだけの造語なので，あしからず，･･･.
それから１モル粒子数が増加したときの自由エネルギー増加量というのは，あくまで単位の取り方としてそう換算しているのであって，実際に１モル増加させるわけではないことを断っておきます。車が時速５０kmで走るといっても実際に１時間かけて５０km走って見せる必要はなく，ある瞬間，瞬間に速度が定義できるのといっしょです。）
[***] 式が本当に同じかどうかは，各熱力学関数がルジャンドル変換という変数変換で結び付けられていることを利用して確認することができます。
ルジャンドル変換 G＝F＋PV， dG＝dF＋PdV＋VdP と dG ＝−SdT＋VdP＋μdn からdGを消去して，
dF ＝−PdV−SdT＋μdn
| これを F(V,T,n ) の全微分 dF ＝−PdV−SdT＋ |  |
∂F(V,T,n) |  |
dn と比較すれば， | ||
| ∂n | V,T | |||||
μ ＝ ∂F(V,T,n) ∂n V,T
これで，一つ目の”＝”が証明されます。以下同様 ･･･ 。
[3-1] ということで，開放系の熱力学関数に関する全微分は，
dU ＝ TdS−PdV＋μdn
dH ＝ TdS＋VdP＋μdn
dF ＝−SdT−PdV＋μdn
dG ＝−SdT＋VdP＋μdn
と書くことができます。
［４］ これらの式からは開放系におけるいくつかの熱力学公式が導かれます。たとえば一番目の
dU＝TdS−PdV＋μdn
を U，V を一定の下で，dn で除せば，
0＝T ∂S U,V ＋μ ∂n
が得られます。この式は統計力学的エントロピーからグランドカノニカル分布を導く際に拠りどころとする熱力学公式です [#]。他にもいろいろな公式が導かれますが，WEB上ではここまでとしておきます。
［５］ 最後に前ページで求めた２相平衡条件[#] の考察をこのページで導入した化学ポテンシャルを用いて言い直しておきます。
まず，７.で求めた各熱力学関数であらわされる熱平衡条件[#]は，開放系では，
開放系の熱平衡条件
ただし，k はすべての相について和をとる。 以前の書き方は誤解が多いのでこのように書き改めた。ホントは広い意味をもたせて，(δF)T,V,n ≧0 などで済ませた方がベストだと思われるが....紛れのないような書き方にした。 (09/08/19) なお，化学反応の関わる開放系はn=一定ではない。 |
と書き直せます。
これらを示しただけでは，これらをどうやって使うのか分からないかも知れません。そこで具体例として，前ページですでに求めた，
（３）等温定圧条件下[#]での２相共存平衡条件をここでの結果をふまえたやり方でもう一度求めてみましょう。
各相α，βとで粒子の交換(=粒子数の変化)が可能であると考えると，
(δG)T,P,n ＝−(S(α)＋S(β))δT＋(V(α)＋V(β))δP＋μ(α)δn(α)＋μ(β)δn(β)
＝(μ(α)−μ(β))δn(α)≧ 0
が熱平衡条件となります。仮想的な粒子の変分δn(α)は，正負どちらでもよいので，この不等式が成り立つ条件は，
μ(α)＝μ(β) ←これは単一成分系では，g(α)＝g(β) と同じイミ
となります。ここで， (δG)T,P,n において，δT＝δP＝0 は，等温定圧条件下なので最初からわかっていることですが，考え方がわかるように明示しました。これが化学ポテンシャルを用いた等温定圧下での単一成分２相系の平衡条件です。
２つの相の間での粒子の交換を許す場合，他の一定とする２変数がいずれであれ，変分δnが関わる項からは２つの相における化学ポテンシャルが等しいという条件が出てくることもわかりますね？
それと，ここで，n＝一定という意味は，n＝n(α)＋n(β) が一定ということ，つまり，δn(α)＋δn(β)＝0 ということであって，決して，δn(α)＝δn(β)＝0ということではないので勘違いしないように。また，V＝一定という意味も，δV(α)＋δV(β)＝δV＝0 ということなどなど････です。
(２)等温等積の場合については演習問題。
答え α＝気相，β＝液相として，
(δF)T,V,n ＝−(S(α )+S(β))δT−P(α)δV(α )−P(β)δV(β)＋μ(α)δn(α)＋μ(β)δn(β)
↓ δT＝0 ，δV(α )＋δV(β)＝0
＝(P(α)-P(β))δV(β)＋(μ(α)-μ(β))δn(α) ≧ 0
これが任意の仮想的変分 δV(β)，δn(α) について成り立つための条件として，
P(α)＝P(β)，および，μ(α)＝μ(β)
が２相共存条件として得られる。
結局，T（一定)，V を変数として，(δF)T,V,n を考えても，
P(α)＝P(β)
μ(α)＝μ(β) ⇔ g(T,V)(α)＝g(T,V)(β) ⇔ g(T,P)(α)＝g(T,P)(β)
のように熱平衡条件は T と P の関数として与えられるのです。
熱力学的自由度とは
理想気体の熱力学的自由度は２です。状態方程式を
PV=nRT
と書いたときに，変数は気体定数Rを除いて4つあることをもって，熱力学的自由度は3であると考えるのは大間違いです。系の分量 と熱力学自由度とは直接関係ないからです。見かけの変数の数にとらわれてはいけません。
気体の状態方程式を，
P=ρRT ρ=n/V ： 密度 mol/L
と書けば，変数の数を数えて熱力学的自由度を2ということは正しいです。すべて，分量に関係ない示強変数 P，ρ，T で表されているからです。
もし，圧力をP＝F/S と力Fと面積Sで表して，状態方程式を
F V＝nRT S
と表して，理想気体の熱力学的自由度が4であると主張することも当然ナンセンスです。
熱力学的自由度は，系の大きさに関係なく，「熱平衡状態を決定するために必要十分な独立変数の数」のことを指しているのです。
1Lの水蒸気と100gの水が1atmで熱平衡状態にある条件は，10Lの水蒸気と5gの水が1atmで熱平衡状態にある条件は同じであり，温度が100℃であることです（どちらの系も熱力学的自由度=1）。やかんに入れた水の量によって沸騰する温度が変わったりなんかしないでしょう？ 水蒸気の量，水の量は熱平衡条件とは直接関係ないのです。
言うまでもないですが，大学の期末試験で，「この系が平衡であるときの水蒸気の体積を求めよ。」という問題を工夫して作ることはできます。しかし，それとこれとは別次元の話です。分かりますか？
