(前書きに代えて)
| 1 用語と公式の覚え方 (前書きに代えて) |
||
| f-denshi.com [目次へ] 更新日: 03/05/24 | ||
| サイト検索 | ||
熱力学が学問的に確立した時期は19世紀前半で,それは産業革命において中心な役割を演じていた蒸気機関の進歩と密接に関係していることは言うまでもありません。高温の物体から熱を受けとり,それを力学的な仕事に変えることを繰り返す機械を総称して熱機関といいますが,19世紀前半の第一線の多くの技術者たちの関心はその効率,つまり熱機関が受け取る熱を仕事に変える変換効率をどうやって高めるかにありました。
この分野が大きく動き出したのは18世紀末,ワットらによる回転動力を発生させる蒸気機関の実用化を契機とします。ワットや同時代の技術者たちは単なる発明家というだけではなく,「ワットの法則」などを含む熱力学理論を展開していました。結局,その当時の熱力学理論は間違いであったということで,現代の教科書には,「熱素」なる妖しい言葉を残す他,全く登場しないのですが,彼らも当てずっぽうでやっていたのではなく,ちゃんと理論的な指針を作りながら蒸気機関の改良に取り組んでいたのです。その当時の理論は,「正解」を探り当てたクラウジウスの研究に多大な影響を及ぼしたことも知られています。他にも,ジュール(イギリス),カルノー(フランス),ケルビン[=トムソン](イギリス)らの功績があって,1850年頃までには現在,私たちが目に触れるような形での熱力学の基本法則が提示されています。さらに熱力学の成熟に歩調をあわせて,現在,内燃機関と呼ばれる様々なタイプのエンジンが19世紀後半に発明されていきました。もし,熱力学の応用が熱機関にだけとどまっていたならば,熱力学の重要性は限られたものであったかも知れません。ところがそこで得られた概念や結果はその後,熱力学の創設者たちが思いもしなかった広がりを見せました。様々な物理現象,化学反応などの解明に威力を発揮しただけでなく,情報処理や哲学の分野にまで多大な影響を与えつづけています。(以上,2008/10/16,改訂)
熱力学史については,山本義隆先生の「熱学思想の史的展開」という本が圧倒的に優れています。もともとは1982?年頃から数年にわたって「BASIC数学」という雑誌に連載されていた記事で実は私はそちらしか読んでませんが。
他には,I・プリゴジン&I・スタンジュール著「混沌からの秩序」(みすず書房)1987年発行 も熱力学史に詳しいです。当ホームページのカルノーサイクルやクラジウスの原理の説明もこの本から大きく影響を受けています。人類が熱機関という革命的な動力を手に入れた高揚感の中で熱力学が生まれ育っていく過程が瑞々しく描かれています。(2021年9月21日)
熱力学の土台は4つの法則から成り立っています。
|
熱力学の原理 ( 証明なしに受け入れる経験則 ) |
|
| 熱力学第零法則 | 熱平衡状態の存在と推移律 |
| 熱力学第一法則 | 集団に対してのエネルギー保存則 |
| 熱力学第二法則 | 熱現象には時間方向性が存在 |
| 熱力学第三法則 | 絶対零度の定義 |
これらにいくつかの実験的な事実を付け加えることで,化学平衡をはじめとする数多くの物理化学現象を説明することができます。
[1] 本文中でも必要の都度,用語の説明はしますが,重要語句(ちょっと難しそうなもの)についてはじめにまとめておきましょう。
| 系 (system) | 考察の対象となる巨視的な物質集団 |
| 外界,周囲 (surroundings) | 上記以外の部分。系の都合に応じて熱,仕事,物質(質量)を交換する。 |
[2] 系の分類
| 外界・周囲との関係 ⇒ | 熱,仕事の交換 | 質量(物質)の交換 |
| 開放系 (open -) | ある | ある |
| 閉鎖系 (closed -) | ある | ない |
| 孤立系 (isolated -) | ない | ない |
他に断熱系がありますが,これは文字通り外界と熱の交換をしない系です。仕事に関してはどちらでも構いません。
[3] 示強変数と示量変数
| 示強変数(関数):系の質量に無関係な性質 (intensive - ) |
温度(T),圧力(P),化学ポテンシャルμ など |
| 示量変数(関数):系の質量に依存する性質 (extensive - ) |
体積(V),内部エネルギー(U),エントロピー(S)など |
[4] 熱力学平衡状態と定常状態
| *** | 示強変数の時間変化 | エネルギー,物質の流れ |
| 熱力学平衡状態 (thermodynamic equilibrium state) | ない | ない |
| 定常状態 (steady state) | ない | ある |
*定常状態の話題はこの講義ではほとんどでてきません。非平衡熱力学で使う概念です。
定常状態の例としては,ヒーターに一定の電流が流れ,一定温度を保ったまま一定の熱を外界に放出し続けているような状態です。
熱力学的自由度は,系の大きさに関係なく,「熱平衡状態を決定するために必要十分な独立変数の数」のこ
| 熱力学的自由度 | 系の大きさ(分量)に関係なく,熱平衡状態を決定するために必要十分な独立変数の数 | |||||||||||
| ギブスの相律 |
|
[5] 状態量と過程の量
| 状態量:熱平衡状態を指定すれば,唯一定まる量 (quantity of state) |
S,P,V,T,U,G,H,F (状態変数,または状態関数),dS,・・・,dF |
| 過程の量:熱平衡状態を動かすための量 (quantity of process) |
W,Q, d'W,d'Q |
始めの状態 A と終わりの状態 ( =A ) が同じで,途中,異なる状態 B を経由するような状態の動かし方:
A ⇒ B ⇒ A (変化)
をサイクル,またはサイクル過程といいます。このとき,系はサイクルによってもとの状態に戻らなければなりませんが,外界は変化しても構いません。
もし,熱力学状態を鉄道の駅に例えると,各駅の標高は状態量です。どうやってその駅にたどり着いたかには関係なく,一つ駅を指定すれば,唯一定まる量だからです。他方,駅から駅へ移動するために必要な運賃は過程の量です。出発駅と到着駅の両方とその経路を指定しないと値が定まりません。東京から名古屋へ行くための運賃は,どのルートで行くか,何に(各停,新幹線,特急)乗って行くかで違ってしまうからです。
状態量の微小変化は微分記号を用いて,dS,dP,・・・ のように書きます。一方,過程の量の微小量は,d'W,d'Qというように d' という記号を慣用的に使います。その理由は先ほどの例を用いて説明すると,駅と駅との距離を小さくとったとき,状態量である標高差は小さくなるのに対して,過程の量である運賃は必ずしも小さくならないからです。つまり,東京から隣の有楽町まで行くための運賃が初乗り運賃だと決め付けるのは早合点であって,東京を出発し,松本を経由して名古屋に出て,そこから熱海,品川と経由して有楽町にやってくるときの運賃というのもアリだからです。つまり,過程の量とは数学的な微分量という概念とは馴染まないのです。だから, d という記号を使わないのです。それでもどうして小さな過程の量⇔少ない運賃(=130円)というものを考えたいときがあります。そのようなとき,d' という記号を使います。
状態量の微小量を完全微分,過程の量の微小量を不完全微分と言う説明もありますが,本文中[#]で説明しています。
[6] 平均モル量と部分モル量
| 平均モル量:示量変数を系のモル数で割った量 (mean molal property) |
平均モル体積 ( v = V/n ),もしくはモル体積 平均モルエントロピー( s = S/n ) |
||||||||||||||||||
| 部分モル量:示量変数をP,T一定の下で系のモル数で偏微分 (partial molal property) |
|
ここで,偏微分,
∂V ∂nj T,P,ni≠nj
の右下に添え字で,T,Pなどがついてますが,これはnで偏微分する際,変数T,Pなどを一定とすることを意味しています。数学ではこの添え字をたいてい省略しますが,熱力学ではしばしば独立変数の取り方に任意性があるため省略しないことが普通です。
| 注意: 多くの教科書では,部分モル量を表すのに, 「 v~ 」ではなく,「 |
|
」 を用います。 |
WEBの文章の中で後者の記号を多用するのは入力が大変なので前者を使いました。
[7] 系に及ぼす〜作用(〜接触))
| 熱的作用 | 熱伝導,熱放射(赤外線) |
| 機械的作用 | 力学的,電磁気的な力(ローレンツ力など) |
| 質量的作用 | 物質交換 (蒸発のような相転移) |
電磁波の照射が熱的か機械的かは,ビミョーなケースも多いのではないかと思います。意図的に磁性体材料を多量に含む液体に変動磁場をかけて対流を引き起こせば,これは機械的作用と呼んで良いでしょう。一方,電子レンジで”チ〜ン”するのは熱的作用。
[8] 均一系と不均一系
| * | 系内の示強関数の性質 | 系内の界面 | 相の数 |
| 均一系 (homogeneous system) | 空間の連続関数 | ない | 1つ |
| 不均一系 (heterogeneous system) | 空間の不連続関数 | ある | 2つ以上 |
ここで,相 (phase) とは示強変数が連続関数であらわせる領域の数です。均一系を単相系,不均一系を多相系とも言います。似たような用語に純粋系と混合系がありますが,これらは系に含まれている分子の種類(=成分)の数によって分類しています。前者は1成分のみ,後者は2成分以上の分子を含んでいます。具体的な成分の数によって,単一成分系,2成分系,・・・などとも言います。また,相の数,成分の数とを組み合わせて,2成分2相系などいうようにも使います。
[9] 最後になりましが,もっとも重要な単語の定義です。
| 熱 | 系の(内部)エネルギーを増減させる仕事以外のエネルギーすべての総称 |
熱力学の勉強がまったくの初めてという人はこの節は読み飛ばしてもいいでしょう。次の「2状態方程式と内部エネルギー」から読み始め,「8 熱力学関数」のところまで進み,またここへ戻ってきてじっくり読んで実践することをお奨めします。一方,熱力学2度目の挑戦という人はここで,熱力学関数の”構造”を理屈ぬきできっちり頭に焼き付けてしまう方がベターでしょう。「暗記などけしからん」と言ってる場合ではないので。木を見ず森を見るのがここでの目的です。
[1] 熱力学でつまずく最大の原因は似たような熱力学関数がたくさん現れるため消化不良を起こすことではないでしょうか。主要な熱力学関数の公式は熱力学第一法則を次々とルジャンドル変換[#]してゆくことで得られるために高度な対称性を持っています。(そのためどれも似かよっていてかえって覚えられないのですが,・・・)そこで,熱力学が苦手という方は下の図を必要なときすぐに書き下せるように覚えることを強く推奨します。この図がどれほどの優れモノかは,後々わかることと思いますが,この図を覚えるだけで熱力学をだいぶ理解した気になれることは保障します。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
まず,この図の覚え方ですが,この図のすべてを暗記する必要はありません。この表の中心の8つのアルファベットの並びだけ覚えればOKです。覚え方もあります。
[ (Z字に)SPVT,(十字に)UGHF ]
と100回唱えるのです。「すっぱいブトー,ウガンダ,ハイフン」という呪文も追加すればなお記憶は確実に。
なお,ウガンダとはアフリカのタンザニアの隣国です。タンザニアはどこにあるかといえば,ケニアの隣(この3つの国は隣りどおし)で,その国境にアフリカ最高峰の山,キリマンジャロ(5895m)があります。
[2] この8文字のアルファベットの並びを覚えておくと,その周辺に散らばっている熱力学関数の基本関係式(全微分)は,機械的に書き出すことができます。
「 たとえば,ギブス自由エネルギー dG は,
|
(1)G のすぐ近くの変数P と T が独立変数, |
⇒ dP,dT, |
| (2)ただし,下段の変数 T にはマイナスつける | ⇒ dP,-dT |
| (3)それぞれたすきがけの位置の V と S が係数に | ⇒ VdP−SdT |
これで, dG = VdP−SdT が得られます。他の熱力学関数の全微分,
dH=TdS+VdP
dU=TdS−PdV
dF=-SdT−PdV
も(1),(2),(3)の手続きで書き下すことができます。自分で確かめてみましょう。これだけ覚えれば他の熱力学公式は正攻法で計算してもたいした手間なく導けます。
ルジャンドル変換と呼ばれる水色で示した熱力学関数間の関係式もこの図で覚えることができます。たとえば,Fから→Gへ変換するとき,すなわち,G=F+?と表したいとします。このとき,図のF→Gの方向の矢印が右上がりですが,図中の同じ右上がり/で結ばれた赤い変数PとVに注目します。その積PVが?の部分となります。つまり,G=F+PV として,FからGへの変換式を得ます。
他方,GはHを用いて,G=H+?と表すこともできます。図を見ると,H→Gは右下がりです。右下がりに並んだ赤い変数はTとSです。この積が?に対応するのですが,今度は→が下がっているので,マイナス符号をつけて,G=H−TSとしなければいけません。要点を標語にすると,
(1) 右上がりは右上がり。(右下がりは右下がり,左上がりは左上がり,左下がりは左下がり。)
(2) 上がるときプラス,下がるときマイナス。
以上,ゴロよく覚えましょう。すべての結果を表にすると,
| (1) U = H−PV | (1)' U = F+ST |
|
|||||||||||||||||||||||
| (2) H = U+PV | (2)' H = G+ST | ||||||||||||||||||||||||
| (3) F = G−PV | (3)' F = U−ST | ||||||||||||||||||||||||
| (4) G = F+PV | (4)' G = H−ST |
[3] さて,先ほど得た4つの全微分の公式から,割り算だけで次のような関係がただちにでてきます。例えば,
dG = VdP−SdT において,温度一定 ( dT = 0 ) として,両辺 dP で割れば,
| ∂G | = V が得られます。同様に次の関係を必要に応じて導くことができます。 | |||
| ∂P | T |
|
|
||||||||||||||||||||||||||||||
|
|
(さらに次の ”規則” を知っていれば,他の公式も書き下ろすことができます。)
[4] マックスウェルの関係式は熱力学変数の1階偏導関数について成立する等式ですが,先程の図(下に再掲載)に,分母,分子を隔てる線を縦(垂直)か横(水平)に書き込めば一発ででてきます。ただし,縦に線を入れたときはマイナスをつけてから等しいとします。
具体的に一つ例を示せば,横に
| H | |||||
| S |
|
P | |||
| U | 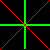 |
G | |||
| V |
|
T | |||
| F |
S P V T
と切ります。この場合,分母のV,Tを独立変数とした,”水平切り” なので符号は+であることに注意すれば,
⇒ ∂S =+ ∂P ∂V T ∂T V
ということになります。残りの式も同様に下のとおり得られます。
|
||||||||||||||||
|
||||||||||||||||
|
||||||||||||||||
|
ほとんどの場合,水平切りか垂直切りで用が足りるのですが,たまに斜め切りが必要となります。そのときに役立つのが次の公式です。
| ∂P | ・ | ∂V | ・ | ∂T | = | ∂V | ・ | ∂T | ・ | ∂P | =−1 | ||||||||||||||||||
| ∂V | T | ∂T | P | ∂P | V | ∂P | T | ∂V | P | ∂T | V |
これは,解析学では陰関数定理[#]と呼ばれているものです。
SUSTAINABLE TOKIWADAIGAK SINCE 2002