７　熱平衡の条件
f-denshi.com 　［目次へ］　更新日： 08/6/19

ここでは，一般的な系(←純粋気体に限定しない系)の熱平衡条件(＝熱平衡条件)について考察します。その際，新しい熱力学関数として，ヘルムホルツ自由エネルギーとギブス自由エネルギーを導入します。

１．熱平衡条件

［１］  熱力学第二法則を認めると熱平衡状態の予測･判定が可能になります。熱力学第二法則法則によれば，孤立系とみなせる十分広い範囲(大風呂敷を広げるなら全宇宙)で考えるときは，系の状態が，

A₀ ⇒ A₁ ⇒ A₂  ････  ⇒ A_n　

と自然に変化してゆくならばそのとき，各状態での全エントロピーは遂次増加しているはずで，

S₀ ≦ S₁≦ S₂  ････ ≦ S_n

という不等式を満たしていなければなりません。ということは，エントロピーを状態 A_k の関数として， S(A_k)と書くならば，関数 S(A_k)に極大を与える状態A_maxに達すると，系はもうそれ以上，自発変化が起こらないということができます。もし，状態A_maxの近傍の異なる状態A_max＋εに変化しようとするとエントロピーが減少することになり，熱力学第二法則に反するからです。このような，それ以上，

「自発的に変化しない状態を熱平衡状態と呼びます。」

　例えるならば，”状態” の動ける範囲と初期値を指定してやると，上を向いて登ることしか知らない ”状態” は上へ上へとエントロピーの山を駆け登り，最初に到達したピークで立ち往生することになる･･･これが熱力学第二法則から予想される自然に起こり得る現象の帰結です。

［２］　このような考察を状況に応じて定量的に取り扱うと，様々な熱平衡条件を導くことができます。まず，最も一般的な熱平衡条件は次のように言えるでしょう。

「系が平衡状態にあるときは，すべての仮想的な状態の変化について計算される系のエントロピー変化が熱力学第二法則に反する。」　

式で書くと，

といえます。この式は，熱力学第二法則：　dQ/T ≦ dS　の不等号の向きを変えて，d の変わりδと置き換えたものです。δ記号を使うのは変化量があくまで ”仮想的な変分量” であることを強調ためです。この式があらゆる熱平衡条件を求めるための出発点となる式です。この[*]式に様々な条件をつけることでいろいろな条件付熱平衡条件が導出されます。

［３］　まず，この不等式は熱の出入りのない(δQ＝0)仮想的変化に対しては，

を意味し，孤立系の熱平衡状態においては，すべての仮想的な状態変化に対して，エントロピーが減少する。つまり，その状態のエントロピーは極大値となっていることを示しています。(極大値と最大値とは同じ意味ではありませんぞ。)　　

［４］　次に熱平衡条件　δQ−TδS ≧ 0　を状態変数だけで表すために，δQ＝δU＋PδV　[#]　を [*] に代入してみましょう。すると，熱平衡条件として，

δU＋PδV−TδS ≧ 0　　　　　　　　　　　 ････････････     [**]

が得られます。ここで条件，δS＝δV＝0 を課すと，

これから等エントロピー･等積変化しか許されないという条件下での熱平衡条件は内部エネルギーが極小であるということができます。エントロピーの性質，すなわち，熱力学第２法則から出発し，内部エネルギーに着目した熱平衡条件が導かれました。

［５］　次に系になされる仕事が体積変化によるものだけのときは，エンタルピー変化は δH＝δU＋PδV＋VδP と書けることを思い出しましょう[#]。この関係式と[**]からδU＋PδV を消去すると，

δH ＋VδP−TδS≧ 0　　　　　　　　　　　　 ････････････     [***]

ここで，δP＝δS＝0と条件を課せば，

が等エントロピー，定圧変化における熱平衡条件となります。　一方，[**]，[***]においてそれぞれ，δU＝δV＝0，δH ＝δP＝0 とすれば，

も示すことができ，これは孤立系の熱平衡条件と同じになります。つまり，エントロピー増大の法則が文字通り成り立つのは次のような条件となります。

拘束条件	一定とする 変数	熱平衡の条件	自発変化が 起こるとき
断熱変化(すべての孤立系で)	Q	S が極大：δS ≦ 0	dS ≧ 0
等内部エネルギー･定積変化	U，V
等エンタルピー･定圧変化	H，P

　そしてこれらの条件が満たされない場合，必ずしもエントロピーが極大のところで熱平衡状態が達成されるわけではないということになります。そのような場合，もはやエントピーは熱平衡状態を記述する最良の指標とはならないのです。新しい熱力学関数を熱力学の舞台に引きずり出してこなければならない理由がここにあります。また，ここで導いた内部エネルギーやエンタルピーを極小とする熱平衡条件も等エントロピー変化というものが実験にどうやって実現させるのか難しいところがあります。したがって，ここまで直接議論されなかった温度という実験的制御が容易な熱力学変数を熱平衡の議論の中に取り込んでゆく必要があるのです。

２．ヘルムホルツ自由エネルギー

［１］　温度・体積が一定の場合の熱平衡条件を考えましょう。この場合，注目している系は一般的に外界と熱を交換するので，熱力学第二法則を適用するときに外部熱源も含めた全体を考える必要があります。

温度，体積一定の場合，熱平衡条件は一般的な熱平衡条件 [**] δU＋PδV−TδS ≧ 0　を書きなおして，

(δU)_T,V−T(δS)_T,V　≧　0　　　　

となります。もちろん，熱平衡条件としてこの表現でもOKですが，もっと簡潔に表現するために次のような状態量 F を定義します。

F ＝ U−TS

この微小量を考えると，

δF ＝δU−TδS−SδT

T，Vを一定とするときは，

(δF)_T,V＝(δU)_T,V−T(δS)_T,V

これをもちいると，先ほどの不等式は，

と簡潔になります。このF をヘルムホルツ自由エネルギーといいます。この用語を用いると，温度，体積一定のもとで系が熱平衡にある条件はヘルムホルツ自由エネルギーが極小となることということができます。

一方，自発変化が起こるならば， (dF)_T,V≦0ということができます。つまり，自発変化にともなってヘルムホルツ自由エネルギーは減少するのです。　　

［２］　ヘルムホルツ自由エネルギーには応用上，重要な意味があります。熱力学のもともとの関心事は熱機関に投入した熱をできるだけ多く ”使いものになる” 仕事(エネルギー) として取り出したいというところにありました。それではいったい理論的にどれくらいまで取り出し可能かというと，それは熱力学第一法則と熱力学第二法則とを組み合わせた式，

d'Q ＝ dU −d'W ≦ TdS　

を，

系が外へする仕事：  −ｄ'W　≦ −dU＋TdS

と書き直してみるとわかります。左辺は系が外部へ行った仕事，右辺がその取り出せる仕事の限界(最大値)を示しています。この右辺をヘルムホルツ自由エネルギーを用いて書き表すと，−ｄ'W　≦−dF−SdT　となりますが，等温変化(dT＝0)のときは，

−d'W	≦	−dF	［等温変化］
(系が外部へする仕事)		−(ヘルムホルツ自由エネルギー変化)

とできます。つまり，熱機関を(連続して運転するときには温度が上昇し続けたたり，下がり続けたりすることはないので)一定の温度下で連続運転する(＝系をサイクルする)ときに取り出せるエネルギーの最大値はヘルムホルツ自由エネルギー変化の値で制限されることがわかります。そのようなわけで　F　を別名，最大仕事関数といいます。もし，dFが負であるならば，−dFは正の値となり，系が外部に対して行う仕事も正の値を取り得ます。しかし，dFが正であれば，決して−d'Wは正の値を取ることができず，外へ対して正の仕事を行うことができません。

［３］　さて，等温，等積下で自発変化が起こるとき，条件付の熱力学第二法則からdF≦0でなければならないことを述べましたが，その際，系は外部に対して仕事を行うこともできます。ではこのとき，エントロピーはどう変化するのでしょうか。エントロピーは増えることもあれば，減ることもあるというのが結論です。その様子を，(dF)_T,V＝(dU)_T,V−T(dS)_T,V に注意して分類すると次のようになります。

エントロピーが自発的変化によって増大するのは，あくまで断熱系での話であって，適当な条件下ではエントロピーが減少しながら，自発的な変化が進行していくこともあり得ます。この図は上にゆくほどヘルムホルツ自由エネルギーFが高くなるように描いていますが，(a)の場合，dF＜0となる推進力は内部エネルギーの減少によるもので，−TdSは正，すなわち，エントロピーは減少(dS＜0)しており，自発変化を妨げる働きをしています。この分，系が外部に対して行える最大仕事（-dF）は減少しているのです。つまり，−TdSは，系から仕事として取り出すことのできないエネルギーとなっており，束縛エネルギーと呼ばれることがあります。ただし，この項がいつも取り出せないわけではなく，(b)のように外部に取り出せるエネルギーの主要部分となることさえもあります。その具体例として濃淡電池の放電反応を例としてあげることができます。(c)は内部エネルギーの減少とエントロピーの増加がともに自発変化に有利に寄与するという場合です。

３．ギブス自由エネルギー

［１］　次に系の温度一定に追加する条件として，圧力が一定の場合を考えましょう。すなわち，等温(δT＝0)，定圧(δP＝0)変化しか許されないときの熱平衡条件を求めます。生命現象も含む多くの実験が大気圧，室温の下で行なわれることを考えるとこれはもっとも重要な条件です。一般的な熱平衡条件 [**]を書きなおして，

(δU)_T,P＋P(δV)_T,P−T(δS)_T,P ＝ (δH)_T,P−T(δS)_T,P　≧　0　　　　　　　　　　　　･････[***]

と書くことから始めます。この不等式もギブス自由エネルギーと呼ばれる新しい熱力学関数 G を定義することで簡潔に書き直します。すなわち，

G ＝ U＋PV−TS 　 ＝ H−TS

を定義すると，

δG＝(δU)＋P(δV)＋V(δP)−T(δS)−S(δT)
　　　↓
(δG)_T,P ＝ (δU)_T,P＋P(δV)_T,P−T(δS)_T,P　
　　　　  ＝(δH)_T,P−T(δS)_T,P

すると，熱平衡条件[***]は，

と簡潔に書き直せます。つまり，等温，等圧における熱平衡条件はその状態のギブス自由エネルギーが極小となっていることです。逆に自発変化が起こるならば，そのとき， (δG)_T,P≦0ということができます。つまり，自発変化に際してギブス自由エネルギーは減少していくのです。　　

ヘルムホルツ自由エネルギーの場合と同様な議論なので詳述は避けますが，等温･定圧変化において，dG＝dH−TdSであることに注意して自発変化の起こる場合のギブス自由エネルギー変化を下図のとおり分類可能です。

ここでも dF を考えたときと同じように，ギブス自由エネルギー変化 dG に対するエントロピー項の寄与はケースバイケースであって，dGの温度依存性も正･負の両方が考えられます。

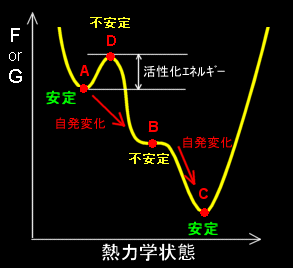［1-2］　さて，右の図を用いて熱平衡とその熱力学的安定性について吟味してみます。横軸は連続的に移り合える熱力学状態を表し，縦軸をその状態に対応するヘルムホルツ自由エネルギー，またはギブス自由エネルギーとしています。そして点A，B，C，Dは，系が互いに移り変われる自由エネルギーの第一変分δFが0，すなわち，その点でFが極値をとる可能性のある点です。これらの点が本当に極値をとるかどうかはさらに第二変分δ²F の符号を調べて見る[#]必要があります。第二変分が正，すなわち，下に凸となる点は，先の４つの点の中ではAとCであることがわかります。

「熱力学的に安定な点AとCは熱平衡状態となり得る。」

と言えます。点Bは第二変分は0，点Dの第二変分は負であり，熱力学的安定点ではありません。実際に系がAとC，どちらの熱平衡状態に達するかは，系に与えられる初期条件に依存し，たとえば，最初に系がAとDとの中間あたりにあれば，Aが熱平衡状態として落ち着く点となります。これは，熱力学第二法則からの直接的な表現，「自発変化がおきる場合，dG,dF≦0となる」ということからの帰結です。

しかし，もっと広い範囲で熱力学状態を考えれば，条件 dF≦0 は，

A　→　B　→　C　　　　　　　　　　　[自発的変化の方向]

という変化が自発的に起るということも可能です。つまり，十分な時間が経過すれば，Aにあった状態はB，さらにCへと変化することが自然な方向であると熱力学第二法則から主張できます。その意味では，「状態BはAより安定な状態」ということができますが，この場合の安定という用語は第二変分から議論される熱力学安定性とは異なった意味で使われていることに注意しなければいけません。

　　なお，状態Bが状態Aより安定であるからといって，AからBへの変化が現実に観測できるかどうかは別問題です。熱力学第二法則がいうところの自発変化は，いわば時間が無限大経過した時の状況を述べているのであって，人間にとって現実的な時間経過後の状況を述べているわけではないからです。AからBへの変化にはDを通らなければいけませんが，DはAより，大きな自由エネルギーを持っています。したがって，活性化エネルギーとも呼ばれるAからDへ至るためのエネルギーが十分大きいならば，実質的にAからBへの変化を見ることはできないのです。どれくらいの時間をかければどれくらいの確率でこの変化を観測可能かというようなことは平衡熱力学において予言することはできません。このような問題は反応速度論や量子統計力学の助けが必要となります。

［２］　最後にこれまででてきた熱力学関数を用いて示される熱平衡条件をまとめておくと，

拘束条件 一定とする 変数 熱平衡の条件 自発変化が 起こるとき 等エントロピー等積変化 S，V U が極小：δU ≧ 0 dU ≦ 0 等エントロピー定圧変化 S，P H が極小：δH ≧ 0 dH ≦ 0 等温等積変化 T，V F が極小：δF ≧ 0 dF ≦ 0 等温定圧変化 T，P G が極小：δG ≧ 0 dG ≦ 0

H S P U G V T F

となります。具体的な熱平衡条件を求めるときの実際の数学的手続きは，δG＝0　などとおき，必要条件を求め，十分条件については第２変分についてδ²G＞0 を確認することとなります。詳細は，Appendix　３　熱平衡状態の安定性のところで確認してください。

なお，右側に再掲した ”ウガンダハイフンの図” をもう一度確認してください。熱平衡条件に見られる美しい対称性もこの図から見てとることができます。

［目次へ］

CopyRight　フジエダ電子出版