| 9 純物質の2相平衡 | ||
| f-denshi.com [目次へ] 更新日: 09/01/22 蒸気圧曲線の図を書き換えました。 | ||
| サイト検索 | ||
このページではいくつかの均一な系が複数集まって平衡状態にある不均一系を考察の対象に加えていきます。均一な系一つ一つを相といいますが,熱力学の言葉では,「示強変数が(空間的に)連続的に変化する領域」として定義されます。たとえば,室温で水の上に水とは異なる物質,ヘキサンが浮かんで接触している場合は,水の相とヘキサンの相の2つからなる不均一系です。水の相とヘキサンの相の間には界面が存在し,これを境に密度のような示強変数は不連続に変化します。この2つの相の間では熱,体積などは交換しますが質量 (物質) は交換しません。一方,水の中に同じ分子から構成される物質である氷が浮かんでいる場合も同じく2つの相からなる不均一系といえます。しかし,この場合,2つの相の間で質量(=水分子)の交換も起こりえます。
ここでは後者の場合で,もっとも簡単な1種類の分子しか存在しない不均一系の熱平衡について考えてみましょう。
[1] nモルの単一成分からなる物質(=1種類の分子だけ含む)が2つの相 に共存して,熱平衡にある状況(=2相平衡状態,または2相共存平衡状態という)を考えます。例えば水蒸気と水 が容器の中で共存して熱平衡にある状況を思い浮かべるとよいでしょう。
(1) 断熱条件下での熱平衡
まず,この系が体積V一定の断熱容器の中に孤立して存在している状況(1)を考えます。そのとき,この系に課せられている拘束条件は,k相(k=α,β)の物質のモル数をn(k),k相の内部エネルギーをk相にある物質のモル数n(k)で割った平均モル内部エネルギーをu(k),同様に求められる平均モル体積をv(k)とすると,
n=n(α)+n(β) =一定 ⇒ δn(α)+δn(β) = 0
U=n(α)u(α)+n(β)u(β)= 一定 ⇒ −n(β)δu(β) =δn(α)(u(α)−u(β))+n(α)δu(α)
V=n(α)v(α)+n(β)v(β)= 一定 ⇒ −n(β)δv(β) =δn(α)(v(α)−v(β))+n(α)δv(α)
と表されます(拘束条件)。そして,孤立系に対する熱平衡条件をこの系に適用するために,この系の全エントロピー を考えます。相α,相βの1モルあたりのエントロピーを
s(α)=s(α)(u(α),v(α)),
s(β)=s(β)(u(β),v(β))
とすると,系全体のエントロピーは,
S=n(α)s(α)(u(α),v(α))+n(β)s(β)(u(β),v(β))
と書くことができます。その変分は,
| δS=s(α)δn(α)+s(β)δn(β)+n(α) | ∂s(α) | δu(α)+n(β) | ∂s(β) | δu(β)+n(α) | ∂s(α) | δv(α)+n(β) | ∂s(β) | δv(β) |
| ∂u(α) | ∂u(β) | ∂v(α) | ∂v(β) |
↓ 公式(9)’[#],δU=TδS−PδV,
| =s(α)δn(α)+s(β)δn(β)+ | n(α) | δu(α)+ | n(β) | δu(β)+ | n(α)P(α) | δv(α)+ | n(β)P(β) | δv(β) |
| T(α) | T(β) | T(α) | T(β) |
↓ 初めに示した3つの拘束条件を用いて,
| =(s(α)−s(β))δn(α)+ | n(α) | δu(α)− | δn(α)(u(α)−u(β))+n(α)δu(α) | + | n(α)P(α) | δv(α)− | δn(α)(v(α)−v(β))+n(α)δv(α) | P(β) |
| T(α) | T(β) | T(α) | T(β) |
| = | 1 | − | 1 | n(α)δu(α)+ | P(α) | − | P(β) | n(α)δv(α)+ | s(α)−s(β)− | u(α)+P(β)v(α) | + | u(β)+P(β)v(β) | δn(α) | ||||||
| T(α) | T(β) | T(α) | T(β) | T(β) | T(β) |
[2] この最初2つの項からδS=0であるために必要条件として,
T(α)=T(β)=T
P(α)=P(β)=P
および,最後の項からは T(α)=T(β)=T, P(α)=P(β)=P なので,(δn(α))/Tで括ったその係数から,
s(α)T−u(α)−Pv(α)=s(β)T−u(β)−Pv(β) ⇔ g(α)=g(β) ← G=U+PV−STを参考に [#]
とかけます。ここで,g(α),g(β) は各相における1mol あたりのギブス自由エネルギー(平均モルギブス自由エネルギー)を意味していますが,より一般的には後に出てくる化学ポテンシャルと呼ばれる概念を介して理解する必要があります。
結局,断熱条件下で,一定体積に閉じ込められている水と水蒸気が平衡に到達している場合の2相平衡条件は,
となります。
[3] 同じく水と水蒸気が熱平衡にある条件を,(2)等温等積,(3)等温定圧の拘束条件下での純物質の2相平衡条件についても,(1)と同様に求めて(演習問題),まとめると次表のようになります。
単一成分系の2相平衡
拘束条件 (一定にする変数) 2相平衡条件 (1)断熱条件
全粒子数
内部エネルギー
全体積n=n(α)+n(β)
U=n(α)u(α)+n(β)u(β)
V=n(α)v(α)+n(β)v(β)T(α)=T(β)
P(α)=P(β)
g(α)=g(β)(2)等温等積条件
全粒子数
全体積
温度n=n(α)+n(β)
V=n(α)v(α)+n(β)v(β)
T=T(α)=T(β)P(α)=P(β)
g(α)=g(β)
(3)等温定圧条件
全粒子数
圧力
温度n=n(α)+n(β)
P=P(α)=P(β)
T=T(α)=T(β)g(α)=g(β)
まず,最初に注意してほしいことは,平衡であるために水蒸気と水の比率,n(α)/n(β)がいくらでなければいけないというような,各相のモル数に関する平衡条件がいずれのケースにおいても含まれておりません。このことは,1気圧の下で沸騰するやかんの中のお湯や蒸気の温度がやかんに残っている水の分量に関わらず,常に100℃であるという経験的事実と照らし合わせればもっともなことでしょう。つまり,単一成分系では,各相のモル数やその比は熱平衡状態を特徴付ける変数ではないのです。
一方,3つのケースすべての拘束条件下での2相平衡条件として,各相における1molあたりのギブスの自由エネルギーが等しい,すなわち,
g(α)=g(β)
という等式が共通してでてきますが,これは偶然ではありません。それにはきちんとした理由があり,多成分系で威力を発揮する化学ポテンシャルと呼ばれることになる重要な概念の萌芽をここに見ていることになります。
2つ以上の異なる成分(異なる分子)を含むもっと複雑な系についての熱平衡条件を考察するためには,化学ポテンシャルについてより正確な定式化を行う必要があり,後ほどじっくり議論します。(2相平衡条件:g(α)=g(β)は単一成分系の場合にだけの条件式で,より普遍的には,2つの相の化学ポテンシャルが等しいという:μ(α) =μ(β) とすべきことが後ほどわかります。)
では,n(α)とn(β)との関係はどのように決まるのでしょうか。これは,2相平衡条件だけを考えているだけでは定めることができません。2相平衡条件下ではどのような比であっても構わないからです。これを定めるためには相転移に伴う潜熱を考慮する必要があります。つまり,水から水蒸気へ相転移する際の気化熱が,その状態に到達するまでにどの程度,系に加えられたか,もしくはその逆の液化に伴う熱の放出がどれくらい行われたかによってn(α)/n(β)が定まるのです。
熱平衡条件が,g(α)=g(β)のみによって与えられる3番目のケースについてその様子を図に描いておくと下のようになります。そして,系に加えられた熱量Qとn(α)/n(β)との関係は物質ごとに異なっているのです。つまり,同じ1モルであっても水をすべて水蒸気にするために必要な熱量とアルコールをすべてをアルコール蒸気にするための熱量は一致しないのです。個々の物質の個性ともいえる気化熱の具体的な値を知らなければ,n(α)/n(β)を求めることはできないのです。
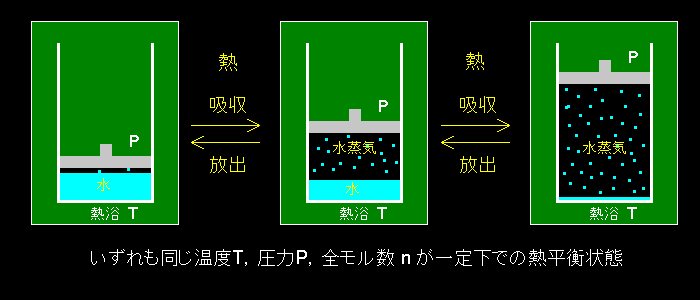
↑ やかんの水が1気圧100℃で沸騰して蒸発するようす(のモデル)。
系に加えられた熱Qによって,気体分子がδn,全体積がδV増加すると,
Q−PδV=δn (u(気体)-u(液体)) だけ内部エネルギーが増加する。)
この図の意味するところは,熱平衡状態でモル比n(α)/n(β)がふらつくということではなく,熱平衡状態に達していれば,n(α)/n(β)は一意的であるが,どのような値を取るかは2相共存平衡条件だけからは予測することはできないということです。 系に出入りした潜熱を考慮して全内部エネルギーUを算出し,全体積V,全粒子数nを指定すればモル比n(α)/n(β)も含めて熱力学状態が定まるということも可能です。ただし,これも単純に熱力学変数をT,P,nではなく,U,V,nに選べばよいという話ではなく,あくまでも潜熱の熱力学体系への導入が,n(α)/n(β)の記述には欠かせません。そして,残念なことに熱力学的理論からは個々の物質の気化熱を導くことは不可能で,実験によって決められるパラメーターです。
|
熱力学は相転移点で破綻しているのか? (初学者にはちょっと高級) 別の例として,始状態として,温度T,圧力P0にあるnモルの水 (←内部エネルギーU=nu(液)は既知!) を, (1) 温度Tの熱源に囲まれた容積Vの真空容器中へ 間仕切りを取るなどして投入した場合を考えます。しばらく放置すると,水の一部は徐々に蒸発して2相共存平衡状態に達します。このとき,系の温度を一定に保つためには熱源から系への熱の移動が必要となります。この熱q は液体の水から気体の水蒸気への相転移に伴う潜熱です。この実験で気体は自由膨張し,仕事をしませんので,先ほどの例 ( T,P一定下での潜熱) とは少し意味が違います。ここで注意すべきことは,このq の値はn,V,Tを定めれば物質ごとに確定値を取りますが,決して熱力学の原理に基づいて予測することのできない量です。これは実在物質の比熱が熱力学の中では実験によってのみ定まることと同じで,潜熱も同様だからです。 ここで,このq が与えられることで,2相共存平衡に達したときの水蒸気のモル数n(気) (当然,水のモル数n(液)も) が一意的に定まることを見ておきましょう。液体状態の水の内部エネルギーの圧力依存性が無視できるとして,熱力学第一法則より, ΔU={n(液)u(液)+n(気)u(気)}−nu(液)=q ここで,u(液),u(気)は平衡状態における水と水蒸気の平均モル内部エネルギーです。ここで, n=n(液)+n(気) であることを用いればすぐに,
であることがわかります。また,平衡に達したときの圧力は,気体が理想気体の状態方程式に従うとして,
となります。以上のようにT,Vを変数とする場合であっても,2相共存平衡状態における水と水蒸気のモル比は,実験によって導入される潜熱q の値を知って初めて求めることが可能なことがわかります。 一方, (2) 真空断熱容器に水を投入 したときは外界から熱の流入がないために,部分的気化によって平衡に達した時の系の温度は低下することになります。その温度幅を予測するためには,水の内部エネルギーの具体的な温度依存性が必要となりますが,これも実験を通して初めて得られる物性値で,熱力学体系の中で導くことはできません。この状況は,熱力学の第一法則や第二法則や各種の熱力学公式をどれだけいじりまわしたところで水の比熱を算出できないことと同じです。 つまり,熱力学には巨視的な変数を用いることによる限界があって,物質の個性が関与する定量的現象の予測に対してはある意味,無力であり,その部分は実験値から定まるパラメーターを天下り的に導入しないと,理論的な予測ができないということです。 300Kの水を301Kに上昇するために必要な熱量は実験によってのみ決定されるのであって,熱力学体系の中で計算することはできません。大学の試験問題で,はじめに300K付近での水の比熱を既知として与え,1K温度を上昇させるに必要な熱量を計算せよということはあり得るでしょうが,それでは話が逆転していることはわかりますね。 ただし,熱力学の予測可能性に限界があることと熱力学体系が破綻しているということはまったく別の話です。ここで,考えているモル比n(α)/n(β)が熱力学平衡条件から定めることができないのは,「熱力学は相転移が起きる点で破綻しているからではなく,限界にぶつかっているから」です。水から水蒸気への気化熱などがわからなければ,具体的にn(α)/n(β)は計算できないということです。気化熱というのは物質ごとに違う個性的なもので,理論予測においてそのような値を必要とするn(α)/n(β)は平衡熱力学の体系から自然に導かれてくることはないということです。 この状況は2相平衡の記述に使う変数をT,P,n からU,V,nなど他の変数の組に変更したからといって解消されるものではありません。Uの中に実験的にしか決められない「潜熱」を表面上隠すことは可能ですが,それは熱力学の問題を解く上での解決策にはなっていません。モル比n(α)/n(β)が熱平衡条件だけから定まらないのは変数の取り方の問題ではなく,もっと熱力学の本質に基づいてそのようになっているのです。 (11/03/25 追加)。 |
最後にもう一つ注意しておくと,ガスコンロに火がついた状態で,ボコボコやかんのお湯が沸騰(突沸)している状態は熱平衡状態ではありません。その状態では系に熱が流入し続けており,水が水蒸気に変化しつづけている状態だからです。あくまで,熱平衡状態とは巨視的な変化が何も起こらない状態を指しているのであって,ガスコンロの火は止めて議論すべきです。それから室温で,コップの水が蒸発してなくなるのも熱平衡状態(2相平衡)を観測しているわけではありません。雨を降らせている雲(霧)の中にでもいないかぎり,地上で H2O の安定な相は気相,つまり,水蒸気なんです。気相-液相の2相共存状態と捉えるのは間違いです。大気圧1atmの中身はほとんど窒素や酸素などで水蒸気の分圧はずっと低いからです。 じゃあ,なぜ,海の水はなくならないかって?それは天の恵みのおかげでしょう。感謝!感謝! この辺は08/09/26 に追記
このように2相共存状態では,n(α)とn(β)はある意味でいろいろな値をとることができるのですが,そのような熱平衡状態を実現できる圧力,温度はまったく自由というわけでなく,g(α)=g(β) という2相共存条件から制約を受けています。次にクラウジウス-クラペイロンの関係式と呼ばれるこの制約下での2相共存状態にある系の圧力と温度の満足すべき条件式を求めてみましょう。
[1] 相転移の定義を厳密に述べておきます,系の温度,圧力などの熱力学変数を連続的に変化させた時にいくつかの性質(比熱,膨張率,電気伝導度,密度など)が不連続に変わることがあります。例えば,1atmにおかれた水の相を室温から100℃を超えて昇温させると水蒸気になり,密度や比熱は不連続的に大きく変わります。この現象を相転移といいます。そして熱力学変数P,T,V,(多成分系ではさらに組成も含めなければいけない)を座標とするグラフにこのような不連続点をプロットしたものを相図,または状態図と言います。相図は高次元空間 (3次元以上) にある図形を何らかの工夫で平面に投影して表示されるので,その規則を理解しておく必要があります。
さて,1.で求めたように純物質の液相と気相とで2相平衡状態にあれば,つまり,液相と気相が共存するとき,それぞれのモルあたりのギブス自由エネルギーは等しくなければなりませんでした。つまり,
g(液)(T,P)=g(気)(T,P)
の関係が成り立っていなければなりません。この関係を満たすような T と P を
T-P 平面に曲線として図示したも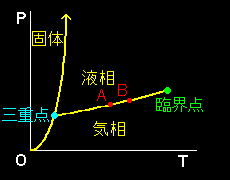 のを蒸気圧曲線といいます。液相,気相に限らず,異なる2相間に対する一般的な用語は2相共存曲線といいます。曲線という理由は,一つの成分からなる均一系の自由度は2です[#]が,このモルあたりのギブス自由エネルギーが等しいという条件式が課せられると,自由度は1つ減って1となるからです。
のを蒸気圧曲線といいます。液相,気相に限らず,異なる2相間に対する一般的な用語は2相共存曲線といいます。曲線という理由は,一つの成分からなる均一系の自由度は2です[#]が,このモルあたりのギブス自由エネルギーが等しいという条件式が課せられると,自由度は1つ減って1となるからです。
さらに3相が共存する点を考えることもできますが,そこでは自由度がさらにもう一つ減って0となり,三重点と呼ばれます。そのときの値 (Pt,Tt) は物質固有の定数です。このように系の成分数,相の数が与えられたときの熱力学自由度については,ギブスの相律と呼ばれる一般式が存在しますが,ここでは純物質の2相共存下での熱力学自由度は1ということだけ確認しておいて,詳しい説明[#]は後回しにしましょう。
[2] 液相と気相の共存する場合に話を戻しましょう。その共存曲線は,T,P,どちらを変数とみなすかによって,
沸点の圧力依存: T=Tb(P)
飽和蒸気圧の温度依存: P=P(T)
という2とおりの記述の仕方が存在しますが,ここでは2番目の圧力Pを温度Tの関数とみなす関係式を求めてみましょう。
気-液曲線上にあって,ごく近くの2点A,B のギブス自由エネルギーをそれぞれ,
g(液)(T,P) = g(気)(T,P) A点 ・・・・・(1)
g(液)(T+dT,P+dT) = g(気)(T+dT,P+dT) B点 ・・・・・(2)
とします。(右図参照)
(2) を1次の微小項まで展開して,
g(液)(T+dT,P+dT)≒g(液)(T,P)+ ∂g(液) dT+ ∂g(液) dP ∂T P ∂P T
↓ 熱力学関数公式 (10),(12) [#]
=g(液)(T,P)−s(液)dT+v(液)dP ・・・(3)
g(気)も同様に展開して,
g(気)(T+dT,P+dT)=g(気)(T,P)−s(気)dT+v(気)dP ・・・(4)
この2式を辺々引いて,(1),(2)を用いると,微分量だけがキャンセルされずに残り,
(s(気)−s(液))dT=(v(気)−v(液))dP
書き直して,
dP = T (s(気)−s(液)) = LB dT T (v(気)−v(液)) TΔvB
と書くことが可能です。ここで,
LB≡T (s(気)−s(液))
↓ΔG=0 なので ΔH=TΔS ですね。
= h(気)−h(液)
=ΔhB (1モルあたりの気化エンタルピー変化(気化熱))
ΔvB≡(v(気)−v(液)) > 0
T:沸点
を導入しました。この関係式をクラウジウス-クラペイロンの式(または気液共存曲線,蒸気圧曲線)といいます。
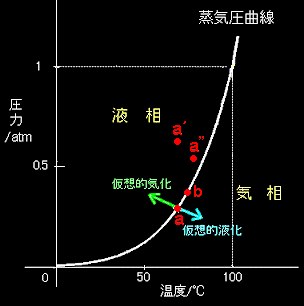 [3] ここでもう一度,1.で議論したやかんの中の水が蒸発する現象について考えてみましょう。水の蒸気圧曲線をラフに描くと右図のようになります。液体と気体が共存する蒸気圧曲線は単調な増加関数になります。これは水が蒸発するときに熱を奪い,水の気化熱LBは正の値をとるからです。
[3] ここでもう一度,1.で議論したやかんの中の水が蒸発する現象について考えてみましょう。水の蒸気圧曲線をラフに描くと右図のようになります。液体と気体が共存する蒸気圧曲線は単調な増加関数になります。これは水が蒸発するときに熱を奪い,水の気化熱LBは正の値をとるからです。
1.では2相共存の平衡条件だけからは水と蒸気の存在比を決めることはできないと述べました。系に熱の出入りがあれば,2相共存平衡を保ったまま,一定の範囲内で水と水蒸気の存在比が変わっていくからです。そのため沸騰しているやかんの中の水の温度は中身がからっぽになるまでずっと近似的に100℃を保っているのです。
その沸騰している温度,圧力で巨視的に変化のない熱平衡状態を実現するためには,熱の出入りを止め,断熱条件とする必要があります。実験的には沸騰しているやかんを100℃で適当な時間だけ加熱を続け,加熱を止めた直後,直ちに断熱材でやかんを囲ってやらなければなりません。(もちろん,やかんのふたはオモリのついたピストンでできており,注ぎ口などあってはならない!)では,本当にこの「2相共存状態」は熱平衡状態として時間変化のない安定な状態なのでしょうか?その答えは先程求めた蒸気圧曲線を使えば,定性的に導き出すことができます。
状態が蒸気圧曲線上の点aにあって断熱条件が課されているとき,仮に液体の一部が蒸発して気体に変化したならばどうなるでしょうか?液体に比べて1モルあたりの容積の大きい気体の割合が増加するので系の圧力は増加します。一方で気化熱によって系の温度は下がるはずです。つまり,図に仮想的気化と示した矢印の方向に状態が移動しようとするはずです。この矢印の先は蒸気圧曲線が増加関数であることを考慮すると必ず液相が安定な領域にあります。言いかえれば,液体の一部に気化が起こると,それを打ち消すように液化が必ず引き起こされるのです。
今度は逆に気体の一部が液化したならばどうなるでしょうか。このときは嵩高い気体分子数が減少するので圧力は減少しようとし,同時に凝集熱も発生して温度が上昇しようとするはずです。ということは,液化が生じると,図の仮想的液化と示した方向,すなわち,気相が安定な方向へ状態が移動して,その液化を妨げようとすることがわかります。
結局,断熱条件を設定したときの水と水蒸気のモル数の比率が,仮にいずれの方向に変化しようとしても,その変化を打ち消すような状態変化が引き起こされることがわかりました。これは,蒸気圧曲線上にある2相共存状態は熱力学的に安定であることを意味しています。
このような熱力学安定性に関する定量的な議論のごく入門的な部分はAppendix3 にまとめてあります(21/10/22)。
ここでいう仮想的と言うのはあくまで仮想的な揺らぎのことであって,実際に2相共存系を圧縮して圧力を上昇させれば液化を引き起こします。このとき,等温条件下ならば系はすべて液体に変化します。これはただ単に図中のa’点では液体が安定ということに相当します。
断熱条件下では,圧力上昇がある一定値より小さければ,部分的な液化による液化熱によって温度が上昇し,新しい2相共存平衡点bに達します。しかし,圧力上昇が一定値より大きければ,系はすべて液体に変化します(a”)。これは熱力学安定性とは全く別の話なので混同しないように。
では,熱力学的に不安定な状態とは,どういう状態を指すのかと言えば,十分時間が経てば,自ずと安定な条件に変化していくような状態で,例としては過冷却状態や過飽和状態などがあげられます。
[4] さて,固-液共存曲線に対する微分方程式もまったく同様に,
dP = (s(液)−s(固)) = LM dT (v(液)−v(固)) TΔvM
LM=T(s(液)−s(固))=h(液)−h(固) (融解エンタルピー変化(融解熱),または凝固熱にマイナス符号をつけたもの)
ΔvM≡(v(液)−v(固))
T:融点
となります。曲線を表す式はそっくりですが,一般に ΔvM は ΔvB に比べて非常に小さいので,固液曲線は気液曲線に比べて傾きが急激になっています。
[5] 固-気共存曲線に対する微分方程式ももこれまでの取り扱いと同様なのはいうまでもなく,結果だけ示すと。
dP = (s(気)−s(固)) = Lv dT (v(気)−v(固)) TΔvv
となります。ここで,
Lv=T(s(気)−s(固))=h(気)−h(固) (昇華エンタルピー変化(昇華熱)
Δvv≡(v(気)−v(固))
T:昇華温度