３　熱力学第１法則と比熱
f-denshi.com  ［目次へ］　更新日： 09/02/01  　
サイト検索

１．熱力学第１法則　

［１］　仕事も熱量も本質的には同じ物理量であり，前回説明した内部エネルギー という概念を介して統合できることを述べているのが熱力学第１法則です。

熱力学第１法則　(エネルギー保存則)
　　熱平衡状態Aにある系に対して，仕事d'Wと熱量d'Qが加えられ，熱平衡状態Bへと変化したとき，

　　系の内部エネルギーの増加 ＝ 系に加えられた仕事 ＋ 系に加えられた熱量
dU d'W d'Q

が成り立つ。

注意：　変数の値がマイナスのときは，「増加」⇒「減少」，「に加えられた」⇒「が与えた」と解釈します。

　ここで，熱平衡状態A，および，Bにおける内部エネルギーをUA，UBとしたとき，その差はdU＝UB−UAとなります。なお，熱平衡状態Aにおける仕事WAとか熱量QAなどという量はナンセンスであり，存在しません。仕事とか熱量 は状態量[#]ではなく，「熱平衡状態を動かすための量」で，過程の量と呼ばれ，その微小量に対しては d'という記号が用いられます。この法則はまた，

熱： 内部エネルギーの変化をもたらす仕事以外のエネルギー形態

という厳密な熱の定義の拠り所となります。

また，この法則を示すためだけならば，あえて微分形で書く必要はなく，

ΔU＝W＋Q

と書いても構わないでしょう。そうすれば左辺が状態量，右辺が過程の量であることからくる微分記号dとd'の使い分けに気を使う必要もありません。ここで，状態量と過程の量についての物理的な意味の違いと数学的な意味の違いがどのように関連しているのか少しわかりにくいので，次のような例えばなしを作ってみました。

　　もし，熱力学状態を鉄道の駅に例えると，各駅の標高は「状態量」です。どうやってその駅にたどり着いたかには関係なく，駅を指定すれば唯一定まる量だからこのように呼びます。他方，駅から駅へ移動するために必要な運賃は「過程の量」です。出発駅と到着駅の両方とその経路を指定しないと値が定まりません。東京から名古屋へ行くための運賃は，どのルートで行くか，何に（各停，新幹線，特急）乗って行くか，その過程によって違ってくるからです。
　状態量の微小変化は微分記号を用いて，dS，dP，･･･　のように書きます。一方，過程の量の微小量は，d'W，d'Qというように　d'　という記号を慣用的に使います。その理由は再び鉄道の駅を用いて説明すると，駅と駅との距離を小さくとったとき，状態量である標高差は小さくなるのに対して，過程の量である運賃は必ずしも小さいとは限らないからです。つまり，東京から隣の有楽町まで行くための運賃が初乗り運賃だと決め付けるのは早合点であって，東京を出発し，松本を経由して名古屋に出て，そこから熱海，品川と経由して有楽町にやってくるときの運賃というのもアリだからです。つまり，過程の量とは数学的な微分量という概念とは本来は馴染まないのです。だから，　d　という記号を使わないのです。それでもどうして小さな過程の量⇔少ない運賃(＝130円)というものを考えたいときがあります。そのようなとき，d' という記号を使います。

以上のような意味の違いをこめて，熱力学第１法則は，

dU ＝ d'W ＋ d'Q

と表記されます。

教科書によってはdUを完全微分，d'W，d'Qを不完全微分と呼ぶことがあります。その数学的な意味は次のようなものです。状態がAからBを結ぶひとつの経路に沿って変化したとき，そのときに加えられた仕事や熱量はAからBへの経路に沿った線積分によって，
W  ＝ A→B 　d'W
Q  ＝ A→B 　d'Q

と計算されるとします。ここで，「'」は線積分を行うべき微小量であることを強調して付けられていると考えてもよいでしょう(しかし，数学のベクトル解析の分野で，「'」を付けるのは一般的ではない)。一方，そのときの内部エネルギーの変化ΔUもAからBへの同じ経路に沿った線積分によって計算されますが，内部エネルギーが状態量（状態関数）であることから，

ΔU＝ A→B 　d'U ＝ UB−UA ＝ 　dU　　　　

と完全微分の積分で書きなおすこともできるのです。ここで，UA，UBはそれぞれ状態A，Bにおける系の内部エネルギーで，ベクトル解析ではこの性質をもつ関数をポテンシャル関数と言います。だから，「数学的には，dU＝d'W＋d'Qと書くのは間違い」とまでは言いませんが，大変，不親切であって，きちんと，

　dU　＝ A→B 　d'W ＋ A→B 　d'Q　［熱力学第１法則］

と積分記号を略さないで書いた方が初学者にはわかりやすいでしょう。このように書けば，「不完全微分どおしを足し合わせて，なぜ完全微分になるのか」などという珍問答が沸き起こることもないでしょう。（このような経緯から私，個人的には不完全微分という用語は使いたくないので，このホームページでは使っていません。蛇足ですが，内部ネルギーが状態量であるのは，内部エネルギーの”個人的事情”によってそうなのであって，仕事や熱量がどのような量であるかには全く何の関係もないことです！　これは先程の駅の標高が状態量である理由と鉄道運賃との間に何の関係もないのと一緒です。）

それからもう一つ，見逃しがちな重要なポイントは，熱力学第１法則は，「どんな変化が起こった場合でも成り立つ」と言うことです。その変化があまりに唐突な場合，そのときの変化を表す経路や仕事量の計算は数学的な線積分で近似することすらできないので，熱力学第１法則は，ΔU＝W＋Q と表す以外に方法はありません。という言い方は，熱力学第１法則に対して失礼であって，「そのような場合でもΔU＝W＋Q と表すことができる」と言った方が熱力学第１法則を正当に評価した真意の伝わる言い方でしょう。熱力学第１法則はスゴイんです！

この熱力学第１法則は，古典力学のエネルギー保存則を普遍化したエネルギー保存則と見ることができます。ニュートンの古典力学をマクロな物体に適用するときは，全く変形することのない剛体球の存在を仮定して，エネルギー保存則を確認しなければなりませんでした。しかし，現実の世界にはそのような物体は存在せず，弾性体であれば必ず変形にともなって熱を発生します。熱力学第１法則は，単に多数の粒子からなる集団に適用される法則という側面からだけではなく，あらゆる現象に適用可能なように古典力学のエネルギー保存則を定式化して述べたものと捉えるべきでしょう。したがって，熱力学第１法則は，特別な条件を課すことなくマクロな系について広く成立する基本法則です。

［２］　熱力学状態を動かす量を過程の量といいました。過程の量は例え，初状態と終状態が同じであっても唯一定まるものではないので途中の様子も含めて明確に指定しなければ熱力学的な議論の対象とすることができません。そこで私たちは理論的な考察を目的とするときはもちろん，実験を行うときも状況を単純化したいがために特定の物理量を一定にして系を変化させることがあります。その条件としてよく使われるのが次の４つです。

　A.断熱変化 （ adiabatic change） ： 外界との熱量の受け渡しがないもとでの熱力学状態の変化。
　B.等積変化 （ isometric change） ： 体積が一定のもとでの熱力学状態の変化。
　C.等温変化 （isothermal change）： 温度が一定のもとでの熱力学状態の変化。
　D.定圧変化 （ isobaric change）  ：　圧力が一定のもとでの熱力学状態の変化。

( isometric の他に isovolumetric も使います。)

A．の下での変化においては文字どおり，d'Q＝0 なので，

dU＝d'W　　　（この場合，仕事も状態量のように扱える。）

ここで，「状態量のように扱える」という意味は，仕事は本質的には状態量ではないが，断熱変化においては，任意の状態に至るまでにある基準点からどれくらいの正味の仕事が加えられたかを状態量である内部エネルギーの変化量を用いて算出できるということです。

B．は多くの場合で系と外界とで仕事のやり取りがない( d'W＝0 )ということと同義語となります。このとき，

dU＝d'Q　　　（この場合，熱量も状態量のように扱える。）

と熱力学第１法則は書き換えられます。ただし，注意すべき点として，系に加えられる，もしくはなされる仕事は体積変化による仕事（＝体積仕事）とは限らないので，そのような仕事が関与する場合は等積変化といえども d'W を落とすことはできません。

［３］　C．D．を説明する前にもう一つ，熱力学においてしばしば，”枕言葉” として使用される重要な語句を説明しておきましょう。それは，

準静的過程　（ quasi-static　process ）

です。「過程」とは，「状態変化」と同義語ですが，前後の状態よりもそのプロセスに関心があるときに使うようです。準静的過程とはいろいろな状態変化のうちで，

（１）　熱平衡状態の記述が状態変化に際して逐次適用できる（正しく成り立つ）こと（連続性）　　
（２）　逆行可能な過程であること。　　　

の条件を満たす過程です。数学的には，「線積分を使って，その過程の仕事量と熱量を計算できる過程」と言った方が実用的かも知れません。

（１）をもっと詳しく述べると，始状態Aから異なる終状態Bへ至る途中の状態として，無限小だけ異なり連続的に連なる無数の平衡状態が存在し，それを順々に辿る道筋が準静的な過程ということになります。このような過程を実際におこうなうとすれば，それは無限にゆっくりと熱力学状態を僅かずつ変化させる操作が必要となります。

（２）の逆行可能の意味は文字通り，その過程の時間の進みを逆転させた現象も実際に起こり得るということです。

これら２つは，仕事や熱量が熱平衡状態を記述する変数についての連続関数であるならば，線積分が可能であり，線積分が可能であるならば，その積分経路を逆行する線積分も可能であり，その値は順方向のものと符号が違うだけであるという数学的内容に対応しています。

具体的には，　　

準静的仕事

実質的には，仕事を微分 ” PdV ” で表すための概念 で，前出の例でいえば，ゆっくりとピストンを動かすことに相当します。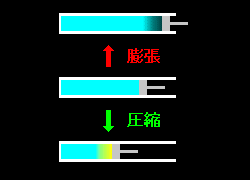
　　　　　
　　　　　実験的な条件：　*　ピストンゆっくり。　
　　　　　　　　　　 　　　　　*　圧力(温度)分布や対流が生じないように。

右図のように気体の密度にムラができる（←このとき熱平衡状態が破れる）ようではダメ，このときピストンに加わる圧力を遂次，実測できたとしても，その圧力を気体の状態方程式　(PV＝nRTなど) に適用することがナンセンスなことは明白です！

もし，（１）が成り立つならば，系の体積が連続的に変化するすべての瞬間において，状態方程式が意味を持ち，状態変化の前後に加えられた仕事をPdVの積分で求めることを正当化します。数学的には，「その経路に沿って連続な関数は線積分可能」ということに対応しています。

準静的熱量の吸収・放出

実質的には，熱量を微分TdSで表すための概念　で，ゆっくり時間をかけた系と熱浴間の熱の移動を意味します。この変数Sとは，もちろんエントロピーと呼ばれる状態量です。ここでは名前だけの紹介に止めておきます。(あとからさんざん出てくる言葉なのでここでは読み流してください。)

　　　　　実験的な条件：　*接する熱浴と系との温度差を小さく
　　　　　　　　　　　　　　　 *圧力(温度)分布や対流が生じないように。

準静的に移動する微小な熱量を，d'Q(可逆) と書くことにします。これは状態量のように扱えるので，「'」を付けなくても良いのかも知れませんが，あまり気にしなくてもいいでしょう。なぜならそのような状況下ではいつもTdS と書くことになるからです。

以上のような準静的な過程を組み合わせることで，過程C．D．を実現することができます。

C．として，理想気体の準静的等温膨張過程を考えてみます。理想気体を膨張させるためにピストンにかかる外圧を気体の圧力Pに比べて微小量δPだけ低い圧力P-δPに設定します。すると，理想気体はδVだけ膨張し，微小な仕事PδVを外界に対して行います。これだけでは熱力学第１法則によって，内部エネルギー，すなわち温度の低下を引き起こしますが，接している大きな熱浴からこれを埋め合わせる分だけの微小量の熱が系に移動して温度を一定に保ちます。ピストンにかかる外圧をさらに微小量低下させて，これを繰り返すことで準静的等温膨張が実現します。

D．の定圧変化として，理想気体の準静的定圧膨張過程を考えます。気体を膨張させるために気体温度Tより，微小量δTだけ高い温度T＋δTの熱浴に系を接触させ，気体温度を上昇させます。このままでは気体圧力が上昇しますが，気体が膨張することで圧力は一定に保つことができます。その際，気体は外界に対して仕事をしますので，その分の熱量が温度T＋δTの熱浴から追加供給されなければいけません。熱浴の温度をさらに微小量上昇させて，これを繰り返すことで準静的等温膨張が実現します。

個人的な悩み：　実質的には，「等温変化は準静的過程の組み合わせによってのみ実現できる」といって構わないと思っていますが，この世には存在しない理想気体の不可逆な自由膨張は等温過程なので，そのように言い切ってしまうと矛盾を引き起こしてしまう。解決方法の一つは理想気体はこの世には存在しないのだから無視しすることにすればよいのだが，そんなことをすると，準静的過程もこの世には存在しないのだから無視しろといわれてしまい，ますます困ったことになる。悩みは尽きない。

［４］　結局，仕事として準静的体積仕事だけ，熱も準静的な出入りだけを考えるのであれば，すべての変数を状態量で表した熱力学第１法則，

dU ＝−PdV ＋TdS

を書き下ろすことができますが，この式を正確に理解できるのはエントロピーの説明の後となります⇒[#]。

最後に，「なぜ，準静的な過程を考えるのか？」という質問に答えておく必要もあろうかと思います。一言で言うと，状態量だけで熱力学を議論したいからです。例えば，仕事d'W を準静的なpdV で表されるものに限ることにすれば，状態量である体積Vを用いて過程の量である系に加えられた仕事を一意的に表すことができるからです。このあとすぐ考察するように一定圧力の下で，体積がVAからVBに準静的に変化したならば，系は，−p（VB−VA） だけ仕事をされたと状態量を用いて計算できるのです。熱量に関しても然りですが，その説明はエントロピーの登場後となります。



２．比熱とエンタルピー

［１］　系の温度を１K上げるのに必要な熱量，すなわち，

d'Q
dT

をその系の熱容量(heat capacity)といいます。コップ一杯の水と浴槽いっぱいの水を１℃上昇させるのに必要な熱量は明らかに違うように，この物理量は系の分量を指定しておかないと，他と実験結果との比較ができません。そこで，モル数当たり，単位重量当たり，単位体積当たりなどさまざまな単位量当たりに換算して示されます。そのような場合，比熱容量とか比熱(specific heat)と呼ばれ，相当する単位によって，モル比熱，重量比熱，容積比熱，・・・　と区別されます。(とはいってもモル比熱を求めるからといってちょうど１モルの試料を使って実験するわけではありません。固体や液体ならば10mgほど量り取ったの試料で熱容量を測定したあとで電卓をたたくことになります。)　また，この値は系に熱を与えるときの条件次第で変わってきますので，その条件を併記することも必須です。実験室でしばしば行われる重要な実験条件として，等積変化と定圧変化があります。ここではこの2つについて考えましょう。

まず，純粋な均一系の熱力学的自由度は２なので，内部エネルギーU は，変数 T と V の関数として，

U ＝ U（ T,V ）　　⇒　　dU ＝ ∂U dT＋ ∂U dV
∂T V ∂Ｖ T

と書いてみましょう。ここで，各偏微分係数の右下の添え字V，およびTは，各変数について偏微分を行う際，定数として扱われる他の変数を明示するためにつけられています。熱力学でよく使われる記法です。

このとき等積変化 dV＝0 であるならば，熱力学第１法則[#]は，d'Q＝dU と書けるので，熱容量は，

Cv≡ d'Q ＝ dU ＝ ∂U 　［等積比熱］
dT V＝一定 dT V＝一定 ∂T V

となります。これを等積比熱 (isometric specific heat )といいます。
(ふつうは系の分量がいくらであるかをあえて指定をせず表記しています。この式のまま必要に応じて1kg当たりの内部エネルギーU [kJ]，比熱Cv [J/gK]というように読み替えればOKです。それからこの定義式やこの周辺の議論は断りのない限り，(1モルの)理想気体に限定する必要はなく，適当量の実在気体を念頭に読んでも構いません。もちろん，この定義は実在液体や固体に適用することもできます。ただし，単に固体の比熱というときは後に述べる定圧比熱をさすことが多い。)

［２］　一方，圧力一定のもとで比熱の測定を行うときは定圧比熱と呼ばれます。加熱によって熱力学状態がAから B に変化する際，系になされた仕事が体積変化のみに由来するならば，熱力学第１法則は，

dU ＝ d'Q−PdV
　　　↓↑
UB−UA＝d'Q−P（ VB−VA ）     　　　　←　U やV ，P は状態量です。
　　　↓↑
d'Q＝｛ UB＋PVB ｝−｛ UA＋PVA ｝　　

と書くことができます。ここで，UA ，UBは系の状態 A，および B における内部エネルギー，また，VA ，VB は系の状態 A，および B における体積であって，最後の式の右辺の変数はすべて状態量であることに注意してください。つまり，d'Q は今の場合，AとBにおける状態量の差となっています。そこで，この状態量を エンタルピーと呼び，

H ≡ U＋PV　　（　⇒　dH ＝ dU ＋ PdV ＋ VdP　）　・・・　[*]　

と定義します。すると，定圧条件下ではd'Q は全微分であり，

d'Q ＝ HB−HA ＝ dH　　←状態量　（定圧変化）

と書くことができます。 (このようにエンタルピーH は定圧条件下での熱力学的な変数の取り扱いの利便性を考慮して定義したものです。しかし，一度 [*] のように定義してしまえば，定義式どおりの関数として他の場面でも使われてゆくことになります。実は奥が深ーいのだ。)

［３］　これより，定圧比熱は，

Cp ＝ d'Q ＝ ∂H 　［定圧比熱］
dT P＝一定 ∂T P

　　　　　　　　（↓　[*]　式でdP＝0　なので）

Cp ＝ ∂H ＝ ∂U ＋P ∂V       ・・・   （1）
∂T P ∂T P ∂T P

と表すことができます。

（参考：　比熱はエントロピーを用いてあらわすことができます　⇒　[#]　）

３．断熱関係式

［４］　最後に Cp と Cv [#] との間に成立する重要な関係式を導いておきましょう。Cp と Cv とは，実験条件が異なるだけで気体（物質）の温度を１K上げるために必要な熱量には変わりありません。したがってどちらか一方がわかればもう片方も求まりそうな気がします。しかし，気体固有の性質も関係してくるであろうことも予想できます。まず，内部エネルギー U(T,V) の全微分から

dU＝ ∂U dT＋ ∂U dV
∂T V ∂Ｖ T
　　＝Cv dT＋ ∂U dV　　　　　　　　　・・・・・　[**]　
∂Ｖ T

圧力 P 一定のもとで，dT で除して，

∂U  ＝ Cv ＋ ∂U ∂V      ・・・　　（２）
∂T P ∂V T ∂T P

（１），（２）を辺々たし合わせると，

Cp と Cv の関係式：　　　　　　　理想気体の場合はこちら　⇒[#]

　Cp ＝ Cv＋ ∂U ＋P ∂V
∂V T ∂T P
⇔
または
Cp−Cv ＝ ∂U ＋P　　・・・（３）
βV ∂V T

ここで，右側の等式を導くために熱膨張率β[#]

βV＝ ∂V
∂T P

を用いました。すると，準静的な仕事のみが関わるときの熱力学第１法則　（ d'Q＝dU＋PdV ）に，[**]を代入し，（３）を用いると，

d'Q ＝ CvdT ＋ ∂U dV ＋ PdV
∂Ｖ T
d'Q ＝ CvdT ＋ Cp−Cv dV　　　　　　［熱力学第１法則 ］
βＶ

と実測可能な量 Cp，Cv，β，V 用いて熱量を表すことができます。

［５］　なお，この式で断熱条件 d'Q＝0　，つまり，左辺を0とした式，

dT ＝− γ−1 dV　；　ただし，γ＝　Cp/Cv　［断熱関係式 ］
βＶ

を断熱関係式といいます。ここで，γは断熱定数と呼ばれる気体物質によって決まる定数です。この式から系の準静的断熱変化における体積の温度依存性を求めることができます。

特に理想気体では，β＝1/T でした[#]。したがって，

dT ＝−(γ−1) dV
T V

積分して，

(γ−1) log V＋log T ＝ (定数)　　
　　　⇔
log(TVγ-1) ＝ 定数

よって，TVγ-1＝定数，および，　PVγ＝定数'　が得られます。これらは断熱曲線と呼ばれます。

理想気体の断熱曲線

　　　　　TVγ-1 ＝ 定数c　　　

　　　　　PVγ　 ＝ 定数c　　ただし，　γ＝Cp/Cv　（＞1）

最後に，この断熱曲線と等温曲線との関係をP-V図上で簡単に調べておきましょう。各曲線を表す式は，

P ＝ nRT 　　　　　　　　等温曲線
V
P ＝ c 　　　　　　　　断熱曲線
Vγ

となります。それぞれの曲線P(V)は，パラメーターT，c を変えることで，P-V図上の曲線群を与えます。今，状態(P0,V0,T0)において，等温曲線と断熱曲線が交わっているとします。このとき，

P0＝ nRT0 ＝ c
V0 V0γ

が成り立ちます，ここで，曲線に沿って膨張させたとき，どちらの方の圧力の低下が大きいのかはこの点での各曲線の傾きを調べてみればわかります。

dP ＝− nRT 　　等温曲線の傾き
dV V2
dP ＝− cγ 　　断熱曲線の傾き
dV Vγ+1

［６］　したがって，状態(P0,V0,T0)において，

　(断熱曲線の傾き)−(等温曲線の傾き) ＝ − cγ − −nRT0 ＝ nRT0 (1−γ) ＜ 0
V0γ+1 V02 V02

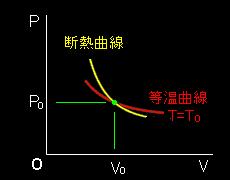つまり，断熱定数γ＞1であることから，断熱曲線の傾きの方が等温曲線の傾きより小さいことがわかります。これらの曲線の傾きがともに負であることを考慮すると，

「断熱曲線の傾きの方が等温曲線の傾きより急峻である。」

といった方がわかりやすいでしょう。P-V線図にすると，次のような関係にあります。これらは後ほどカルノーサイクルの説明に用います。

［目次へ］

メモ書き

d'Q ＝ dH − VdP　　

まだ，エントロピーの話は出てこないが，

κT ＝ − 1 ∂V 　　等温圧縮率
V ∂P T
κS ＝ − 1 ∂V 　　断熱圧縮率
V ∂P S

κT ≧κS＞0

Cp ＝ κT
Cv κS

熱力学と統計力学の関係

「統計力学は新しい学問であり，熱力学は古い学問。だから統計力学を勉強すれば，熱力学は不要である。」と主張する人にときどき出会います。（２０世紀の公理主義の影響かな。）その根拠の一つとして，このページで議論した比熱が原理的に導出できるか否かという事実をあげてきます。しかし，私はそのようなことを根拠にした主張ならば，それは絶対に違うと答えます。不用意に比喩を使うのは好きではないのですが，その理由を代数学の例から一つ示しておきます。
代数学の基本定理というのがあります。

定理：
複素数を係数とするn次方程式(n≧1)，

r0＋r1x＋r2x2＋・・・・＋rnxn ＝ 0

は複素数の中に１つ解をもつ。
つまり，実数を係数とする代数方程式（たとえば，x2＝−１）は実数の中に解を見出せないことがあるのですが，複素数の中で考えるならば，代数方程式には１つ，解が必ず存在するということを主張しています。(もちろん，この定理からすぐにn次代数方程式はn個の複素数解を持つことまでも帰結されます。)　つまり，複素数は究極の数であって，代数学の立場からは，自然数から数を順に拡張していって辿り着いた究極の数が複素数であり，これ以上数を拡張する必然性はないことをも意味しています。
「数学１００の発見」（日本評論社）にも選ばれているたいへん美しい定理です。ベスト１０を選んでもその中に入るに違いないような定理です。しかし，この定理は具体的にその解がどのようなものか教えてはくれません。具体的に求めようとするならば，コンピュータを用いた数値解析に頼るしかありません。もう，私の言いたいことは推測できますね。あることをその学門体系の中で解決できるかできないかで，学問体系の優劣や包含関係を議論することに意味があるとは思えないのです.....。
人それぞれ，いろいろな意見（美学？）があることとは思いますが，「熱力学を知らないと統計力学はちゃんと理解できない。」というのは確実です。熱力学を知らないと，統計力学の教科書にある，
「ここで，熱力学の結果を思い出してほしい。・・・・。したがって，今，我々が導出した・・・は熱力学によるところの・・・に等しいことがわかった。」
というようなの記述を意味不明のものとして読み飛ばすことになります。でもそれだと，統計力学は理解できない。たぶん。絶対かな？
ほんとうは知ってるんだけど，熱力学を知らないことにして，統計力学の理論体系を作っていくことはできるんだろうけど。
追伸：
熱力学と統計力学を分かつ業績を残したボルツマンは，よく知られているように原子が実在すること(その証拠)を知らないままこの世を去った。つまり，実証主義者（＝科学的な態度の持ち主，ワタシのことさー）からすれば，ボルツマンの仕事は空論に過ぎず，ボルツマンもこれに悩んだ。しかし，歴史はその後，ボルツマンの仕事が科学史上，第１級の発見であることを認めることになる。
ということは，科学は正論ばかり言っとってもダメだっちゅうことか？