| 2 状態方程式 | ||
| f-dennshi.com [目次へ] 更新日: 08/08/05 | ||
| サイト検索 | ||
[1] 日常生活で我々がふつう手にとって扱う程度の多数の物質量(数)を巨視的な量といいますが,そのような集団(考察の対象を系,それ以外の部分を外界と呼びます)の挙動をニュートンの運動方程式を用いて解決(記述)することは実質的に不可能です。しかし,熱平衡状態という概念を導入すれば,数少ない変数(パラメーター)で系を特徴付け,いろいろな問題を解くことができるようになります。その学問を熱力学といいます。
[2] 熱力学において使われるもっとも素朴な変数は圧力,体積,温度です。前の2つは特に問題がないと思いますが,温度については少しコメントが必要でしょう。人間が温度という概念を獲得したのは太古の昔ですが,温度に対する正確な知識を得たのはごく最近ことです。
簡単に言うと温度とは物質の種類によらない熱い冷たいという感覚に対応する熱力学変数ですが,温度とこれと似た熱力学変数である熱量とは区別されなければいけません。この2つの違いは,たとえば,水道からとったコーヒーカップ一杯分の水と浴槽いっぱいに張った同じ温度の水をそれぞれ同じ温度のお湯にまでわかすのに必要なエネルギー( =熱量 )が全く違うことを指摘すれば十分理解できることでしょう。
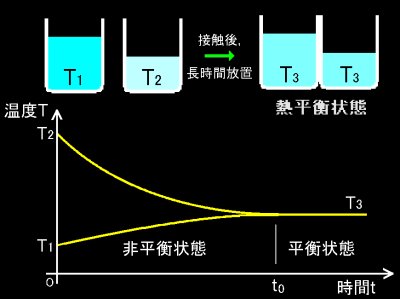
[3] 温度を有意義な物理量として一意的に定義できることは,たとえば私たちが日常生活で,水銀の熱膨張を利用した温度計なるもので様々な物質の温度を定量的に測定し比較できることから疑いありません。このことをきちんと ”公理” として述べたのが熱力学第零法則です。ある2つの物体を熱的に接触させて放置するとそれ以上時間がたっても見かけ上変化の起こらない状態に達することを経験的事実として認めます。そのような状態を熱平衡状態,または単に平衡状態といいます。そのとき,
| 熱力学第零法則 系 A と B が熱平衡状態にあり,系 B と C が熱平衡状態にあるならば,系 A と C も熱平衡状態にある。 |
という主張が熱力学第零法則です。数学で言うところの推移律が成り立つ”何か”を系の中に見出せることを熱力学では出発点におきます。ここでの”何か”とはもちろん温度のことです。 (←正確に言えば温度はその一つで,系によっては様々なパラメーター,圧力,体積,組成,熱力学関数などが熱平衡条件を特徴付けます。)
[4] この法則だけでは,温度の目盛りの振り方は勝手に決めることができ,どのようにも定義可能です。実際,日常生活では国によって摂氏や華氏などいろいろな温度が使われています。このように導入された温度(目盛り)を経験的温度と呼びます。
分子論が確立される以前は”熱素”なるものが接触している2つの物質の間を移動して温度変化が生じると考えられましたが,現在では温度が分子のもつ力学的運動エネルギーの平均値であることがわかっています。そのような観点から「理想気体」なるものを介して定義される温度を絶対温度といいます。
温度が分子の運動エネルギーであるならば,分子が完全に運動を止める状態,つまり,それ以下に下がらない最低の温度というものが存在するはずです。その温度を絶対零度といい,およそ,-273℃です。絶対温度(目盛り)ではその温度を原点(0[K])とし,温度の刻み幅(=1[K]相当のエネルギー)は水の三重点[#]の温度が273.16[K]となるように定めています。単位[K]はケルビンと呼びます。
[5] 熱力学的状態を表すための変数,「温度,圧力」 が体積のような物理量とは ”同質” でないことは,そのまま加算法則(演算)が意味をもたないことからも気が付きます。
例えば,300Kのコップ1杯の水どおしを加えると,体積は2倍になりますが,その温度はやはり300Kのままです。単に100Kと200Kの温度の足し合わて300Kと計算するようなことは算術的には可能でも物理的な意味はないのです。つまり,温度とはその系の分量,もっと正確に言えばその系の質量とは無関係な物理量であることがわかります。
このような物理変数を示強変数(または示強量)といいます。ほかには濃度(組成),密度などがあります。一方,そのままで加減算が意味を持ち,その系のもつ質量に依存するような物理変数を示量変数と言います。先程,温度との対比で述べた熱量は示量変数です。20℃水を90℃のお湯に暖めるために必要なエネルギーは,その水の質量に比例し,コップ2杯の水ではコップ1杯の場合に比べて2倍のエネルギーが必要だからです。
[1] さて,これから熱平衡状態を具体的に記述してゆきたいのですが,しばらくは純粋な気体についてのみ考えてゆきましょう。1モルの気体の熱力学的な状態は気体に関して3つの変数,圧力 P,体積 V,温度 Tを示すことで紛れなく指定することができることにはだれも文句はないでしょう。すなわち,3次元空間内の一つの点を一つの熱力学的状態に対応させることができます。そして,このように熱平衡状態を指定したときに唯一定まる圧力,体積,温度を状態量と呼びましょう。
しかし,実験事実として,独立変数の数はそのうちの 2 つであることがわかっています。これを気体の熱力学自由度は2であると言います。これは熱力学の体系の中では公理と呼ぶべきもので,証明抜きに受け入れることにしましょう。たとえば,気体の状態は圧力 P と温度 T を定めると,残りのもうひとつの気体を特徴付ける量である体積 V は一意的に決まります。このことを数学的には3つの変数の関係で次のように表せます。
(1) V = V(P,T)
または,
(2) f(P,V,T) = 0 ← これは3次元空間の中の曲面の方程式です。
これら気体の熱的性質を特徴付ける方程式を(気体の)状態方程式と呼びます。このように3変数がある関係にある場合,関数 f がどうであれ,
| ∂P | ・ | ∂V | ・ | ∂T | = | ∂V | ・ | ∂T | ・ | ∂P | = -1 ・・・ [*] | ||||||||||||||||||
| ∂V | T | ∂T | P | ∂P | V | ∂P | T | ∂V | P | ∂T | V |
という式が成り立つことに注意しましょう (陰関数定理参照 [#] )。もちろん,各微分係数が存在する範囲での話です。
[2] 一方,(1)式の微分形は,
dV= ∂V dT+ ∂V dP ∂T P ∂P T
となりますが,実験的に測定可能な物理量(パラメーター):
β ≡ 1 ∂V 熱膨張率 V ∂T P
κ = κT ≡ − 1 ∂V 等温圧縮率 V ∂P T
の2つを用いて書き直すと,一般的な気体の状態方程式
気体の状態方程式 [ 実験で測定可能な量だけで表現 ]
|
が得られます。(これは自由度は2であることも示しています。)
[3] また,実験的に得られるもうひとつのパラメーター:
γp≡ ∂P 圧力係数,または熱圧力係数 ∂T V
とは, β=κγp なる関係があります。( [*] を参照 )
[4]気体の状態方程式 f の具体的な関数としては,理想気体と実在気体モデルのひとつ,ファンデルワールス状態方程式(van der Waals Equation) が有名です。
(以後,様々な熱力学関数が出てきますが,この2つの方程式を具体的な計算練習のための教材とします。)
代表的な状態方程式:
Pv = RT, [ 理想気体の状態方程式 ] ただし, v = V/n で,nは気体のモル数,Rは気体定数で,8.31[J /(mol・K)], a,b>0 は気体ごとに定められる定数。 |
||||||||
このように示強変数P,T,v だけで状態方程式を表示すれば,純粋気体の熱力学的状態的自由度が2であることは明白です。ところが,示量変数V,nを用いて理想気体の状態方程式を,
PV=nRT
と書いたとき,nの分だけ1つ自由度が増え,3になったと考えてしまいそうです。もちろん,それは間違いです。1モルというのは人間が分量を表すために勝手に定めた単位量であって,その単位量でもって気体が1モルの時の自由度は2,それ以外のときは3というのではいかにもおかしいでしょう?熱力学では系の分量を表すnを熱平衡状態を定める変数とは考えないのです。
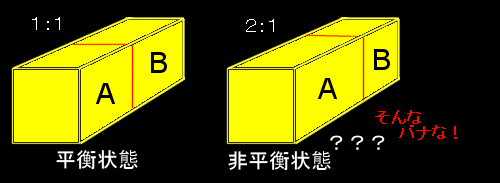
熱平衡状態を記述する状態方程式は,本来,示強変数だけで表わされなければならないはずです。なのになぜ,v→V/nとして示量変数を導入して,PV=nRTと書かれることも多いのか?
それは熱平衡状態の定義そのものにはその分量を指定する必要はないというよりそのようなものを含んでは不都合なのですが,熱平衡状態にある系が別の異なる熱平衡状態に変化する様子を考えるときには系の分量がものをいうのです。
つまり,コーヒーカップ1杯の水と浴槽いっぱいの水とでは,1atm,20℃から1atm,90℃の熱平衡状態に変化するために必要な熱量がまったく違うからです。そのように示強変数と示量変数が使い分けられていることをきちんと意識することはとても重要なことです。
[5] 最後にこの2つの気体モデルについて熱膨張率などを計算すると次のようになります。
- 熱膨張率β 等温圧縮率κ 圧力係数γp 定義
1 ∂V V ∂T P
-1 ∂V V ∂P T
∂P ∂T V 理想
1 T
1 P
P T ファンデル
Rv 3Pv2−2(Pb+RT)v+a
(v−b)v 3Pv2−2(Pb+RT)v+a
R v−b
理想気体,ファンデルワールス状態方程式の物理的な解釈はAppendixにありますが,今は知らなくても構いません。