| 1 多様体の定義 | ||
| f-denshi.com [目次へ] 最終更新日: 22/02/23 校正中 | ||
| サイト検索 | ||
1.位相多様体
[1] 多様体の定義に必要な用語について説明していきましょう。
| 定義 [局所座標 (系)]
位相空間 X の開集合 U から m次元数空間 Rm のある開集合 U’への同相写像, φ: U → U’ を U上の局所座標系 という。また,U とφの組(U,φ)を m次元座標近傍 という。 |
用語:
位相空間 ⇒ [#] を見よ
m次元数空間 Rm (m個の実数の組と考える。m次元ユークリッド空間として読み進めて差し支えない。)
同相写像 ⇒ [#] を見よ
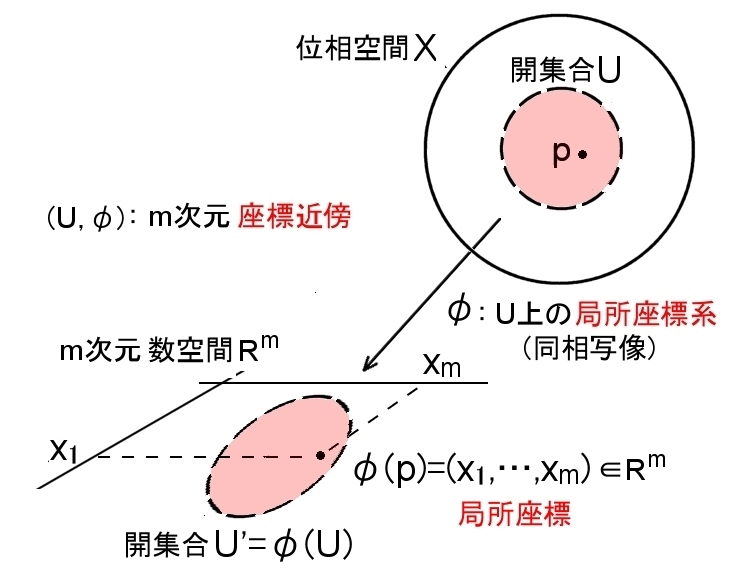
このとき,位相空間の1点 p は同相写像によって,Rmの1点,
φ(p)=(x1,x2,…,xm)
へ写されます。
この (x1,x2,…,xm) を座標近傍 (U,φ)に関する pの局所座標といいます。
やや抽象的ですが,ここに出てきた3つの用語 (↑黄色のゴシック) は繰り返し利用するので,そのまま正確に記憶する必要があります。
[2]
| 定義 [位相多様体]
ハウスドルフ空間 M の任意の点 p について,p を含む m次元座標近傍が存在するとき,M
を m次元位相多様体 という。 |
用語:ハウスドルフ空間 ⇒ [#] を見よ
ユークリッド空間から抽出された距離の公理を満たす空間を距離空間 [#] と言いました。さらに距離空間から開集合の満たす性質を抽出して位相空間[#], なるものを定義しました。
ここで,位相空間としてハウスドルフ空間を持ち出したのは,
ハウスドルフ空間では一意的な点列の収束が保証され,ユークリッド空間の微分に相当する概念 (微分構造) を位相空間に持ち込むことができる
からです。
もちろん,距離空間でも構わないのですが,余計な贅肉をそぎ落とした最低限の本質的条件下で理論を構築するためにハウスドルフ空間を選んでいるのです。
しかし,しばらくはユークリッド空間の部分空間を例に使いながら話をすすめるので,当面,ハウスドルフ空間のかわりにユークリッド空間をイメージしておけば十分です。
[3]
半径1の球面 S2 は R3の部分集合であり,
S2={ (X1,X2,X3)|X12+X22+X32=1}
と定義されます。
ただし,この座標表示は2次元ではなく,3次元の「天空」の座標であり,2次元の局所座標で表示し直す必要があります。
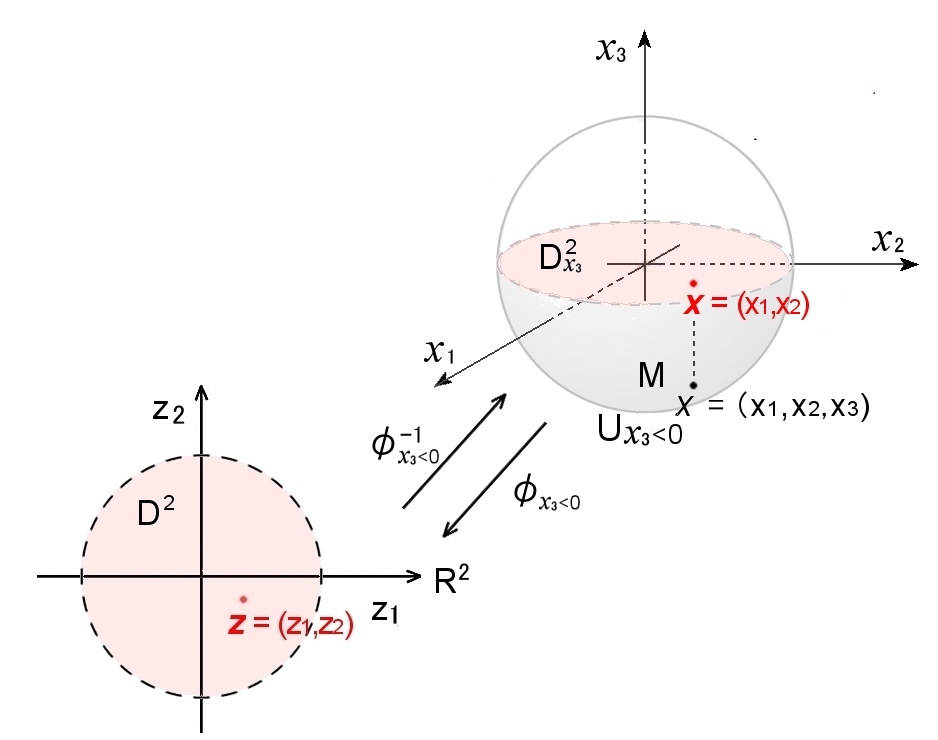
S2の赤道を含まない南半球 Ux3<0 (=多様体 M ) から x1-x2 平面上の半径1の開円板 Dx32 へ射影φx3<0 は同相写像であり,次のように表されます。
x = (X1,X2,X3)∈ Ux3<0 ⇒
φx3<0(x )=(z1(X1,X2,X3), z1(X1,X2,X3))
=(x1,x2) ∈D2⊂ R2 [局所座標表示]
この逆写像は,
z =(z1,z2)∈D2 ⊂ R2 ⇒
φx3<0-1(z ) =(X1(z1,z2),X2(z1,z2),X3(z1,z2))
= z1,z2,-
1−(z12+z22) ∈ Ux3<0 (=M)
[4]
例2
同じ多様体 M −{Ps} に対しての同相写像の例をあげておきます。
ユークリッド空間の球座標を参考にして,
X1 = sinθcosφ,
X2 = sinθsinφ,
X3 = cosθ
のような対応関係を利用します。
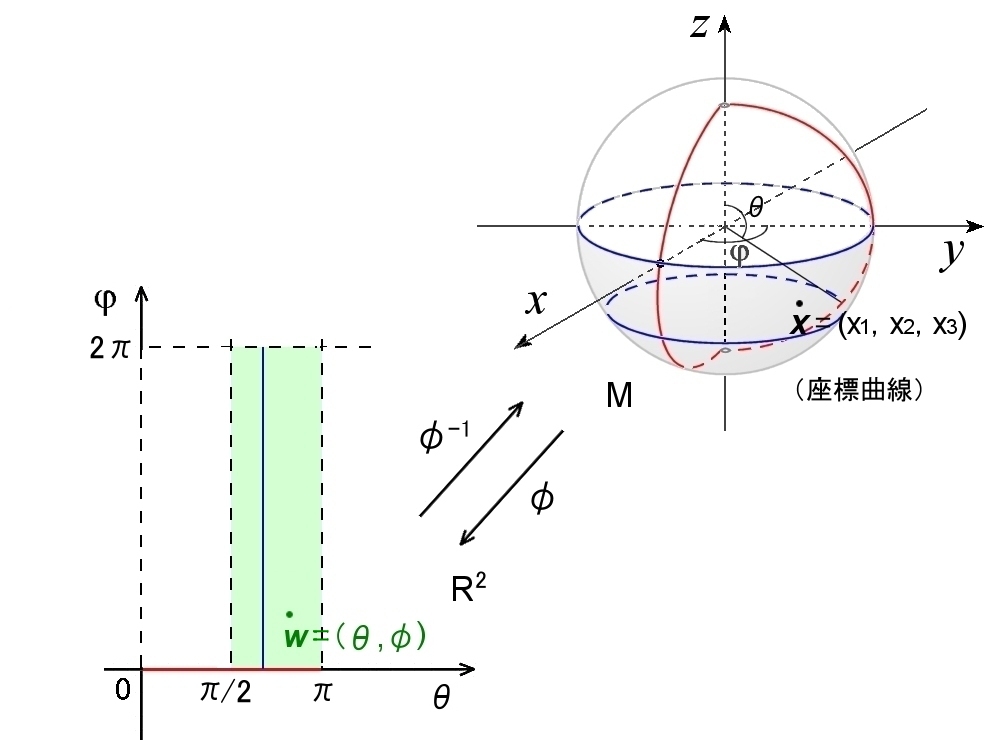
この関係を逆に解くと,
1 = ( X12+X22+X32 )1/2
θ= cos-1( x3/(x12+x22+x32)1/2 )= cos-1( x3)
φ= tan-1( x2/x1 )
ただし, π/2 <θ≦π, 0≦φ<2π。
すると,Ux3<0 から2次元数空間θ-φ⊂ R2 への同相写像を,
x = (X1,X2,X3) ∈ Ux3<0 ⇒
φsp(x )=(θ(X1,X2,X3),φ(X1,X2,X3))
=( cos-1( x3 ),tan-1( x2/x1 ))
∈{ π/2 <θ<π, 0≦φ<2π} ⊂ R2 [局所座標表示]
逆写像は,
w =(θ,φ) ∈ {π/2 <θ<π, 0≦φ<2π} ⊂ R2 ⇒
φsp-1(w )=((X1(θ,φ ) ,X2(θ,φ ) ,X3(θ,φ ) )
= ( sinθcosφ,sinθsinφ,cosθ )∈ Ux3<0
とすることができます。
多様体 M の座標近傍は(U,φ) と表記するとしました [#] が,φの写った先 U’の局所座標を用いて議論するときは,φの代わりにその座標を明記して,
(U,x1,x2,…,xm)
と書いた方が明快です。しばしば,そのように表記することもあります。上の例では座標近傍 (U,z1,z2),(U,θ,φ)のように表します。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
多様体に入る局所座標は一つとは限りません。地図に様々な図法があるように目的に応じて様々な局所座標が導入されます。その様々な局所座標を互いに翻訳する方法が座標変換です。
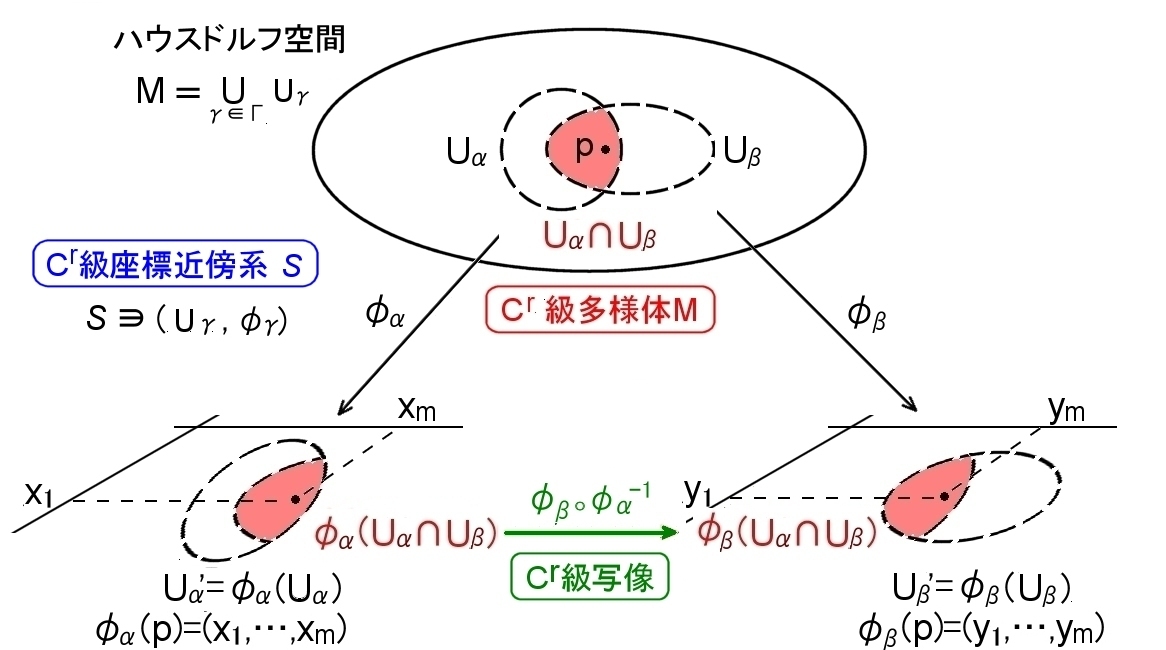
[1] m次元位相多様体M の2つの座標近傍 (Uα,φα),(Uβ,φβ) が共通部分を持っている場合を考えます。その共通部分 Uα∩Uβ にある点 p が,それぞれの局所座標で,
φα(p)=(x1,x2,…,xm)
φβ(p)=(y1,y2,…,ym)
で示されているとします。このとき,局所座標φα(p)と局所座標φβ(p)が1対1に対応するので, (x1,x2,…,xm) と (y1,y2,…,ym) の関係は,
y1 = y1(x1,x2,…,xm)
y2 = y2(x1,x2,…,xm) ← x1,x2,…,xm の関数ということ
…
ym =ym (x1,x2,…,xm)
のように書くことができるはずです。(言うまでもなく,xk=(y1,y2,…,ym) と逆に解くこともできます。) ここで,左辺の yj は局所座標の j 番目の具体的な数値,右辺の yj ( ) は (x1,x2,…,xm) から yj を求める関数を表しています。これらの関係式を座標変換の式といいます。
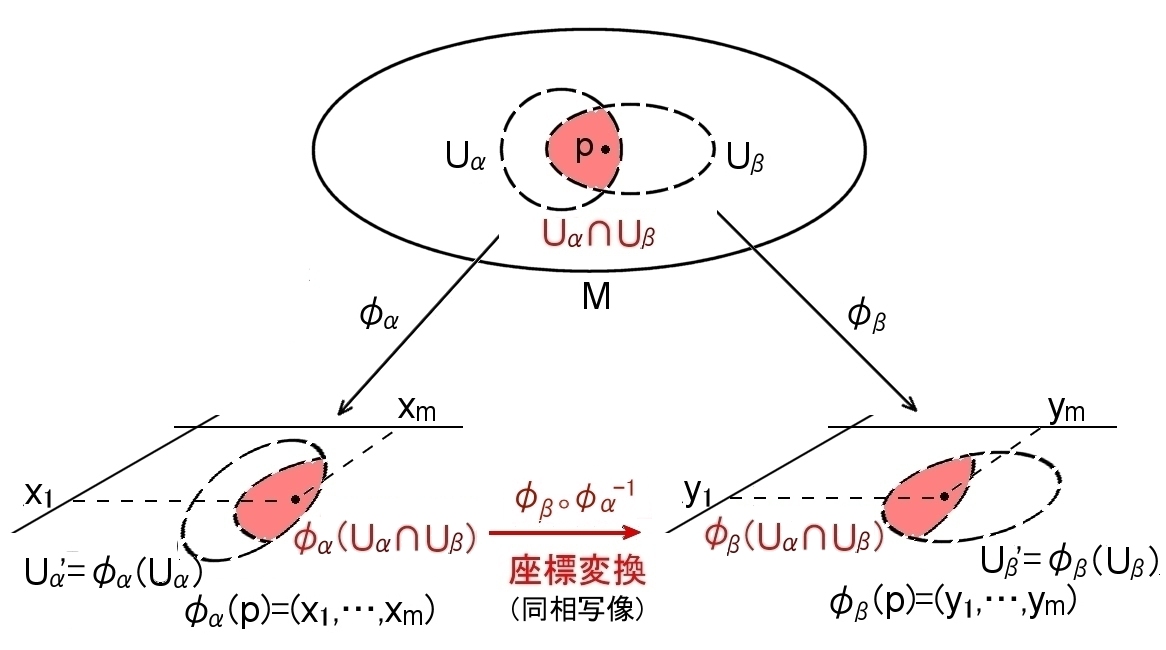
一般的には上図を参考にすれば分かるように,座標変換の式はM上の Uα∩Uβ の領域に定義域を制限した,局所座標系φαの逆写像φα-1と局所座標系φβの合成写像として,φβ゜φα-1 と書くことができます。φα,φβともに同相写像であることから座標変換も同相写像,つまり,上への1対1写像です。
[2] この定義をまとめておくと,
| 定義 [座標変換]
位相多様体 M 上の2つの開集合 Uα,Uβ にそれぞれ座標近傍 (Uα,φα),(Uβ,φβ) が与えられていて,開集合に共通部分が存在するとき, 同相写像, φβ゜φα-1 : φ(Uα∩Uβ ) → ψ(Uα∩Uβ ) を 座標近傍(Uα,φ)から座標近傍(Uβ,ψ)への座標変換という。 |
例3
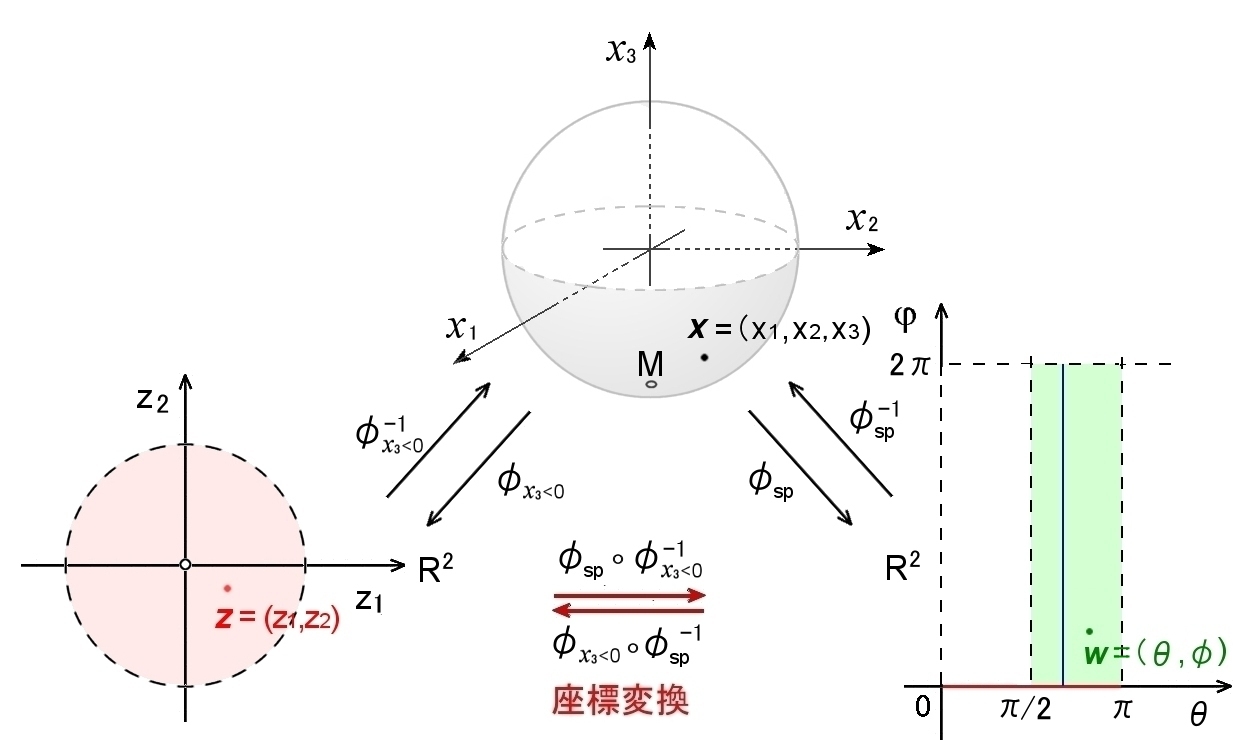
例1,例2の計算結果より
φx3<0-1(z ) = z1,z2,-
1−(z12+z22) =x
φx3<0(x ) =(x1,x2)
φ-1sp(w ) = ( sinθcosφ,sinθsinφ,cosθ ) =x
φsp(x ) =(cos-1(x3), tan-1 x2/x1) )
より,座標変換の式は,
(z1,z2) → (θ,φ)
w =(θ(z1,z2),φ(z1,z2)) =φsp(x )οφx3<0-1(z ) (z1,z2) ← (θ,φ) z =(z1(θ,φ),z2(θ,φ)) |
ここでは,Mの3次元のユークリッド座標 X1,X2,X3 (外在的) が消えて,曲面にふさわしい2次元数空間の座標変換として表されていることに注目してください。
| 定義 [Cr級 (微分可能) 多様体]
位相多様体 M が(m次元)座標近傍の族 [#] {(Uγ,φγ)γ∈Γ} に被覆され[#] , であるとき, S ={(Uγ,φγ)γ∈Γ}を座標近傍系(=アトラス)という。 さらに,Uα∩Uβ≠φ(空集合) であるような任意のα,β∈Γについて, φβ゜φα-1 : φα(Uα∩Uβ) →φβ(Uα∩Uβ) が Cr級写像であるとき, S をCr級座標近傍系, といい,(M,S ) と書く。 |
アトラスとは,一般には地図帳という意味ですが,多様体でのアトラスもまさにそのような意味です。
要するに,座標近傍系(アトラス)とは座標近傍(地図)の集まりということです。そして,
Cr級多様体とは,その 「局所座標間の座標変換の式 が Cr級写像である」 ということです。
具体例として球面を表す多様体について調べてみます。先ほどは南半球だけを考えましたが,ここでは球面全体を考えて,完全な地図帳を作ってみましょう。
例4 6頁からなる球面 S2のアトラスの例
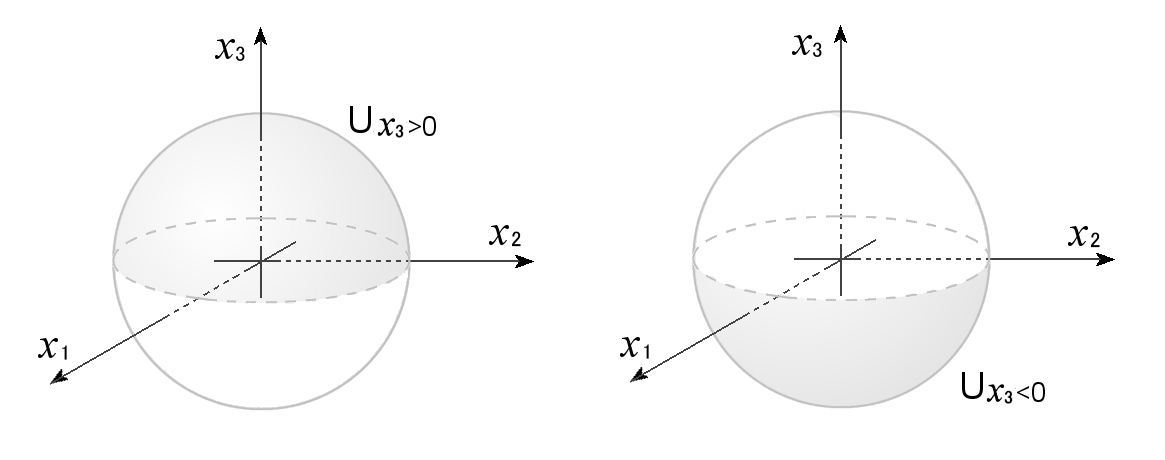
一部繰り返しになります。
S2はR3の部分集合であり,
S2={(x1,x2,x3)|x12+x22+x32=1}
S2の開集合 Ux3>0 を
Ux3>0 ={ (x1,x2,x3) ∈S2|x3>0 }
また,Dx32 を x1x2平面内の半径1の開円板 ,
Dx32 ={ (z1,z2)∈R2|z12+z22<1 }
とします。このとき,x ∈Uz>0 から z ∈Dz2 への対応 ,
φx3>0: x =(x1,x2,x3) → z =(z1,z2)
を x1x2 平面への射影として,
φx3>0(x ) =(z1(x ),z2(x )) =(x1,x2)
と定めます。
[3] この逆関数は,z1=x1,z2=x2 と x12+x22+x32=1 を用いると,
φx3>0-1(z )
=((x1(z ) ,x2(z ) ,x3(z ) )
= z1,z2,
1−(z12+z22)
で表されます。すなわち,φx3>0 は,(1) Ux3>0 から Dx32 への同相写像であることが分かります。
Ux3<0 から Dx32 へ射影φx3<0 も同相写像であり,すでに計算したように,
φx3<0(x )=(x1,x2)
φx3<0-1(z ) = z1,z2,-
1−(z12+z22)
2つまとめると,球面から赤道を除いた部分について,
(1) Ux3>0 ,Ux3<0 から Dx32 への同相写像
が定められます。
同様に,
(2) Ux1>0 ,Ux1<0 から Dx12 への同相写像,
(3) Ux2>0 ,Ux2<0 から Dx22 への同相写像
を考えることができます。
[4] これら同相写像をまとめておくと,
| 局所座標系 と その逆関数 | ||||||||||
| φx3>0(x )=(x1,x2,) |
|
|||||||||
| φx3<0(x )=(x1,x2) |
|
|||||||||
| φx1>0(x )=(x2,x3) |
|
|||||||||
| φx1<0(x )=(x2,x3) |
|
|||||||||
| φx2>0(x )=(x1,x3) |
|
|||||||||
| φx2<0(x )=(x1,x3) |
|
|||||||||
ただし,逆関数の変数∈D2 は,
(z2,z3)→(z1,z2) ← Dx12 ≡D2 の場合
(z1,z3)→(z2,z1) ← Dx22 ≡D2 の場合
と統一した方が見栄えがよいでしょう。(開円板という意味で,Dx12 =Dx22=Dx32 ≡D2 と書く)
また,これらの6つの開集合は位相空間 S2 を完全に被覆して,
S2= Ux1>0 U Ux1<0 U Ux2>0 U Ux2<0 U Ux3>0 U Ux3<0
であるので,S2の座標近傍系 は次の6つの座標近傍 [#] から構成されていると述べることができます。
Sxyz ={ ( Ux1>0,φx1>0),( Ux1<0,φx1<0),( Ux2>0,φx2>0),
( Ux2<0,φx2<0),(Ux3>0,φx3>0),( Ux3<0,φx3<0) }
ただし,これは S2の座標近傍系の一つに過ぎず,次のように別の座標近傍系も存在します。
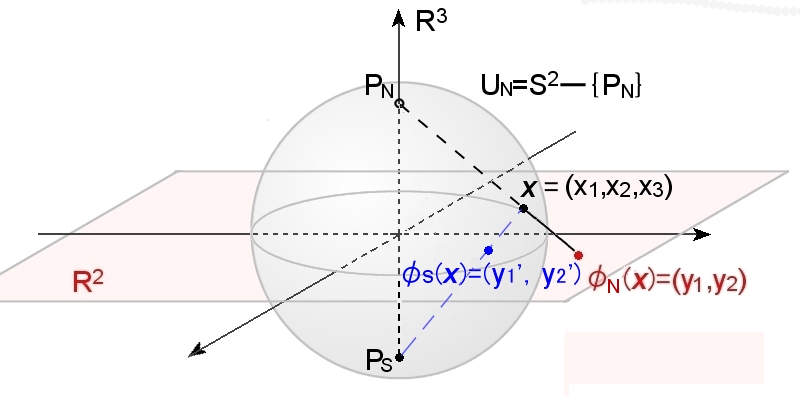
例5 2頁からなる球面 S2のアトラスの例
立体射影を利用します。
単位球面 S2上の開集合の一つをS2から1点 (ここでは北極PN と呼ぶ) を除いた
UN = S2−{PN}
とします。また,そして,PN から UN上の点 x ( この R3での座標を (x1,x2,x3) とする ) を通る直線を考え,その直線が赤道面とよばれる平面 ( R3の3番目の座標 x3=0 で定まるR2) と交わる点を y とします。このとき,x ∈UN から y ∈R2 への対応
φN: x=(x1,x2,x3) → y =(y1,y2)
を立体射影と呼ぶことにします。(下図参考)
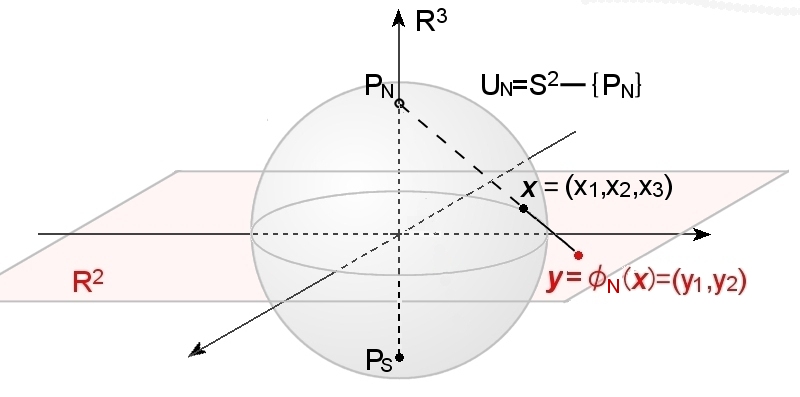
R3 におけるP N とx =(x1,x2,x3) ∈ UN を通る直線のパラメータ t による表示は,
tx+(1-t)PN =(tx1,tx2,tx3+1-t)
この直線が赤道面と交わる点は,tx3+1-t=0 より, t について解き,上式に代入して,第3番目の座標(=0)を無視すると,
φN(x)= x1 , x2 ←同相写像 1-x3 1−x3
となります。ここで,φNは局所座標系で, (y1,y2) が局所座標です。そして,(UN,φN)が S2 の座標近傍ということになります。
一方,この逆関数φN-1(y) は,上式と x12+x22+x32=1 から
φN-1(y)= 2y1 , , 2y2 , y12+y22−1 ・・・・[*] 1+y12+y22 1+y12+y22 1+y12+y22
で与えられます。
[7]
同様に北極点の代わりに,南極点PSを起点にして考えることもできて,開集合
US=S2−{PS}
の立体射影φS,及び,その逆写像φS-1は,UN の場合と同様な計算から
y' =(y'1,y'2)=φS(x)= x1 , x2 ・・・・ [**] 1+x3 1+x3
φS-1(y' )= 2y'1 , , 2y'2 , 1−y'12−y'22 1+y'12+y'22 1+y'12+y'22 1+y'12+y'22
となります。すると,S2= UN ∪ US であり,S2の座標近傍の族,
S NS={ (UN,φN), (US,φS) }
は S2 の座標近傍系となっています。
[8]
次に座標近傍 (UN,φN) から座標近傍 (US,φS) への座標変換の式を求めます。
座標変換可能な範囲は,UN ∩ US =S2−{PN,PS} です。
一方, [*] を [**] 式に代入して,
φS(φN-1(y ))=
2y1 1+y12+y22 ,
2y2 1+y12+y22
1+ y12+y22−1 1+y12+y22
1+ y12+y22−1 1+y12+y22
= y1 , y2 ≡(y'1,y'2) y12+y22 y12+y22
これが座標近傍 (UN,φN) の局所座標 (y1,y2) から座標近傍(Us,φS) の局所座標 (y'1,y'2) への座標変換を表す式です。
この関数はC∞級の関数です。すなわち,
S ={(UN,φN) ,(Us,φS) }
はS は S2 のC∞級座標近傍系です。
S2はC∞級微分可能多様体 (または,C∞級多様体) で,(S2,S ) と書くことができます。
| 定義 [同値]
Cr級多様体 M の2つの座標近傍系 S,T が同値であるとは,S,T との和集合が M上の Cr級座標近傍系となることである。すなわち,S に属する座標近傍とT に属する座標近傍の間の座標変換も Cr級であるとき,2つの座標近傍系 S,T は同値であるという。 また,Mの座標近傍系 S に同値な座標近傍系すべての和集合をM (S ) と書き,S から決まる M の (Cr級) 極大座標近傍系と言います。 さらに (U,φ) が極大座標近傍系M (S)に属する座標近傍であるとき,これを単に Mの Cr級座標近傍という。 |
例1,例2で調べた S2 の2の座標近傍系 Sxyz ,S NS はC∞級の座標変換が存在して同値です。S2の同値な座標近傍系はこの2つだけでなく,他にもたくさん考えることができますが,それらすべての同値な
C∞座標近傍系を含む
M (Sxyz) =M (SNS) =Sxyz ∪S NS ∪ ・・・・
と書いて,S2の (C∞級) 極大座標近傍系と言います。
可微分多様体の存在
1,2,3次元の位相多様体には一意的に可微分構造が入る。
4,8次元位相多様体には可微分構造が入らないものが存在する。
7次元位相多様体には複数の可微分構造が入る。特に7次元球面には28個の可微分構造が入る。
コンパクトで単連結な3次元多様体は3次元球面と同相である。(ポアンカレ予想=ペレルマンの定理)
積多様体
多様体 M と多様体 N の積多様体
M×N
例
T2=S×S トーラス
リーマン球面
双曲幾何学 ロバチェフスキー,ボヤイ,ガウス 曲率<0
楕円幾何学 リーマン 曲率>0