| Appendix 5�@�@�@�ʑ���ԂP�@�Z���� | |
| f-denshi.com �@�m�ڎ��ցn�@�@�ŏI�X�V���F�@ | |
| �T�C�g���� | |
�ʑ���Ԃ̊T�v���܂Ƃ߂Ă����܂��B
�m�P�n�@�܂��C��������i���[�N���b�h��Ԃ��܂ށj�ɂ�����J�W���E�W���͈ȉ��̐�����[#]���Ƃ��v���o���܂��傤�B
|
�J�W���ƕW���̐��� (X�Cd�j�̊J�W���CO1�CO2�CO3�C����C��W���ӁCX���g�ɂ��Ď��̏W���͂������ X�̊J�W���ł���B �iO�P�j�@X�C����сC�� (X�Cd�j�̕W���C�e1�C�e2�C�e3�C����C��W���ӁCX���g�ɂ��Ď��̏W���͂������ X�̕W���ł���B �iF�P�j�@X�C����сC�� |
�����ŁC������Ԃ̊J�W���̐����𒊏o���āC�ʑ���Ԃ����̂悤�ɒ�`���܂��B
|
��`�@�@�@�ʑ��ƈʑ���� X�������W����U [#] �����̏����i�J�W���n�̌����ƌĂ��j���݂����Ƃ��CU ���ʑ��i�܂����J�W���n�j�Ƃ�сCU �̗v�f Uk ���J�W���ƌĂԁB �iO�P�j�@X�C�Ӂ�U �܂��C�ʑ�U ����߂�ꂽ�W��X ���ʑ�����Ƃ�сC(X�CU ) �ƕ\�L����B(�P�Ɉʑ���� X �ƕ\�L���邱�Ƃ������B) |
�����܂ł�����܂��C������ԁiX�Cd�j�̊J�W���nO (d) [#] �͏�̏��������Ă���C
������ԁ@�ˁ@�ʑ����
�����藧���܂��B�ʑ���Ԃ͋�����Ԃ��܂T�O�ł��B
���ɁC
(1) �ŏ��̈ʑ��� {�ӁCX}�@�����ʑ��@�@�@���ł��ア �i�e���j
(2) �ő�̈ʑ��� ��(X)�@�@���U�ʑ� �@�@���ł������i�ׂ����j
�͕K��X�̈ʑ��ƂȂ邱�Ƃ͂����ɂ킩��܂��B�����ŁC��(X) �� X �ׂ̂��W���ł��B
(1)�������ʑ��ƌĂ�C�ł��J�W���̐������Ȃ��܂ށC�ア �i�e���j �ʑ��ł��B(2)�����U�ʑ��ƌĂ�C�ł��J�W���̐��𑽂��܂ލł������i�ׂ����j�ʑ��ł��B
�m�Q�n�@�܂��C(�n�Q)�ɂ�����h�C�ӔZ�x�h�Ƃ́C�L���Z�x�C�Z�Z�x�C�A���̔Z�x�ł��\��Ȃ��Ƃ������Ƃł��B
�Ⴆ�C������Ԃł���������� R �̎��R�Ȉʑ��C���Ȃ킿�C�C�ӂ� p��R �Ƃ̋����� r �ȉ��ł���_�̑S�̏W���ŗ^������J��Ԃ���Ȃ�W�����C���Ȃ킿�C
OR �� {�@(p�|r�Cp�{r)�bp�Cr��R }
�͘A���̔Z�x�����ʑ��ł��B�Ȃ��C��قǏڂ����������܂����C����OR �̒�`�ŁCp�Cr ��L�����Ƃ��Ă��C�����̊J��Ԃ�������̒ʏ�̈ʑ�������i�^����j���Ƃ��ł��܂��B�Ⴆ�C���������J��Ԃ̏���ł����Ă��C�J�W���n�̌����i�O�Q�j����C
(0�C�j��(0�C3) �� (0�C3.1) �� (0�C3.14) U ���
�ƗL����������Ƃ���J��Ԃ̉Z�̘a�W���Ƃ��ĕ\�����Ƃ��ł��܂��ˁB
�m�R�n�@�ł́C�ʏ�̎����̈ʑ��ɑ��āC���J��� ( ] ���J�W���ƔF�߂ĉ�������ǂ��Ȃ�ł��傤���B�����́C����ł�������ƈʑ���Ԃɂ͂Ȃ�̂ł��B���̈ʑ���Ԃ��]���Q���t���C���� (R�COs) �ƌĂ�Ă��܂��B������ƒ�`�������Ă����܂��傤�B
|
��` �]���Q���t���C���� (R�COs) �́C�����̏W�� R �̔��J��ԑS�́C B���o (a�Cb] ��R�bp�Ca��R�Ca��b } ���琶�������W�������ʑ�Os �Ƃ��Ď��ʑ���Ԃ������B(�����J��ԑS��B ���J�� [#] �ɂ�������̈ʑ����) |
�����ŁC�h����������h�W�����Ƃ́CB ���܂݁C�J�W���n�̌��������ł������ȏW�����̂��Ƃ������܂��B��̓I�ɂ́C�����̔C�ӂ� (a�Cb) �̌`�̊J�W�������J��ԂŁC
(a�Cb)��
a�{b�| b �Cb�| b n n�{1
�̂悤�ɕ\����� [#] ���Ƃ��v���o���C�]���Q���t���C�����̈ʑ�Os �ɂ́C�ʏ�̃��[�N���b�h�����̈ʑ�OR ���܂�ł��邱�Ƃ�������܂��B
���̈ʑ���Ԃ́C����Ȍ���ʑ���Ԙ_�̗p���T�O��������邽�߂ɓx�X���p���Ă��炢�܂�
�m�S�n�@�����ЂƂC�v�f�̐����L���ł��� X��{a,b,c}�@�ɂ��ė���グ�Ă����܂��B�܂��CX �ׂ̂��W�� ��(X) �ł����C���̗v�f�������o���ƁC
�ӁC{a}�C{b}�C{c}�C{b,c}�C{c,a}�C{a,b}�C{a,b,c}
��8����܂��B����炷�ׂĂ�v�f�Ƃ��Ċ܂ފ܂ޏW���� U ��O1�@�́C
O 1�F�o�ӁC{a}�C{b}�C{c}�C{b,c}�C{c,a}�C{a,b}�C{a,b,c}�p�@[���U�ʑ�]
�� X��{a,b,c} �̗��U�ʑ��ł���CX �ɗ^������ʑ��̒��ōł������ʑ��ł��B
�t�ɁC��W����X�S�̏W����������Ȃ�C
O 9�F�o�ӁC{a,b,c}�p�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�m�����ʑ��n
�͍ł��ア�����ʑ��ƂȂ�܂��B
���̒��Ԃɂ���ʑ��͗��U�ʑ��̗v�f����ӂ� {a,b,c} ��������6�̗v�f���܂ނ��܂܂Ȃ��� 26��64�̑g�ݍ��킹�ɂ��āC�J�W���n�̌��������邩�ǂ����V���~�ׂ��ɒ��ׂ��������̂ł����C���̂Ƃ���8�^�C�v�C27���K���ł��邱�Ƃ�������܂��B
O 2�F�o�ӁC{a}�C{b}�C{a,b}�C{b,c}�C{a,b,c}�p
�o�ӁC{a}�C{b}�C{a,b}�C{a,c}�C{a,b,c}�p
�o�ӁC{b}�C[c}�C{a,b}�C{b,c}�C{a,b,c}�p
�o�ӁC{b}�C[c}�C{a,c}�C{b,c}�C{a,b,c}�p
�o�ӁC{a}�C[c}�C{a,c}�C{b,c}�C{a,b,c}�p
�o�ӁC{a}�C[c}�C{a,b}�C{a,c}�C{a,b,c}�p
O 3�F�o�ӁC{a}�C{b}�C{a,b}�C{a,b,c}�p
�o�ӁC{b}�C{c}�C{b,c}�C{a,b,c}�p
�o�ӁC{a}�C[c}�C{a,c}�C{a,b,c}�p
O 4�F�o�ӁC{a}�C{a,b}�C{a,c}�C{a,b,c}�p
�o�ӁC{b}�C{a,b}�C{b,c}�C{a,b,c}�p
�o�ӁC{c}�C{a,c}�C{b,c}�C{a,b,c}�p
O 5�F�o�ӁC{a}�C{b,c}�C{a,b,c}�p
�o�ӁC{b}�C{a,c}�C{a,b,c}�p
�o�ӁC{c}�C{a,b}�C{a,b,c}�p
O 6�F�o�ӁC{a}�C{a,b}�C{a,b,c}�p
�o�ӁC{a}�C{a,c}�C{a,b,c}�p
�o�ӁC{b}�C{a,b}�C{a,b,c}�p
�o�ӁC{b}�C{b,c}�C{a,b,c}�p
�o�ӁC{c}�C{a,c}�C{a,b,c}�p
�o�ӁC{c}�C{b,c}�C{a,b,c}�p
O 7�F�o�ӁC{a}�C{a,b,c}�p
�o�ӁC{b}�C{a,b,c}�p
�o�ӁC{c}�C{a,b,c}�p
O 8�F�o�ӁC{a,b}�C{a,b,c}�p
�o�ӁC{b,c}�C{a,b,c}�p
�o�ӁC{a,c}�C{a,b,c}�p
�m�T�n ��̈ꗗ��M�p���Ĉȉ��̐��������Ă��n�j�ł����CO 5 �̈�ԏ�̏W�����o�ӁC{a}�C{b,c}�C{a,b,c}�p��O51 �ɂ��āC�J�W���n�̌��������Ă��邩�O�̂��߃`�F�b�N���Ă݂܂��傤�B
�i�n�P�j�ɂ��ẮC�ӂ� X�� {a,b,c} ���m���Ɋ܂܂�Ă��܂�
�i�n�Q�j�ɂ��ẮC
�Ӂ�{a}��{a}�@�@�@�@�@�@��O51
�Ӂ�{b,c}��{b,c}�@�@�@�@��O 51
�Ӂ�{a,b,c}��{a,b,c}�@�@��O 51
{a}��{b,c}��{a,b,c}�@�@�@��O 51
{a}��{a,b,c}��{a,b,c}�@�@��O 51
{bc}��{a,b,c}��{a,b,c}�@��O 51
(O3)�ɂ��ẮC
�Ӂ�{a}���Ӂ@�@�@�@�@�@��O 51
�Ӂ�{b,c}���Ӂ@�@�@�@�@��O 51
�Ӂ�{a,b,c}���Ӂ@�@�@�@��O 51
{a}��{b,c}���Ӂ@�@�@�@�@��O 51
{a}��{a,b,c}��{a}�@�@�@�@��O 51
{bc}��{a,b,c}��{b,c}�@�@��O 51
�Ɗm�F�ł��܂��B����āC�iX�CO 51 �j�͈ʑ���Ԃł��B
�����������Ă����܂��B
|
���� �ʑ���� (X�CU ) �� X �̕����W�� S ���^����ꂽ�Ƃ��C U |S���oS��U�bU��U �p �� S ���Ƃ蓾��ʑ��̈���ł���B�iU |S ���uU ����U�����ꂽ S �̈ʑ��v�Ƃ����B�j |
��̓I�Ȉʑ���� (X�CU ) �C�������C
X���oa,b,c,d�p�C
U ���o�ӁC{d}�C{a,d}�C{a,b,d}�C{a,c,d}�C{a,b,c,d} �p
���ɐ������܂��BX �̕����W���Ƃ��āC
S���oa,b,c�p
���^����ꂽ�Ƃ��CS��U�@�iU��U �j�@�ׂ�݂�ƁC
U �@���o�ӁC{d}�C{a,d}�C{a,b,d}�C{a,c,d}�C{a,b,c,d} �p
�@�@�@�@�@�@�@�@�@�@�@�@�@���@S��U�@��U�@�@�@ ���@�e�W������v�f d �������悢
U |S���o�ӁC �@�@{a}�C {a,b}�C {a,c}�C {a,b,c} �@�p
�ł��邱�Ƃ�������܂��B�����ŁC����̈Ӗ����邱�Ƃ́C(S�CU |S) �͈ʑ���Ԃł���Ƃ������Ƃł��B
(S�CU |S) ���ʑ���Ԃ̏���(O1)�C(O2)�C(O3)�����Ă��邱�Ƃ͂����Ɋm�F�ł��܂��B�i�ʑ���ԁi{a,b,c}�CO 4�j�Ɠ������B�j
���̂悤�ɁC�v�f�i���W���j�̈ꕔ���o���ē���ꂽ�ʑ���Ԃ���������i�܂��������ʑ�����j�ƌ����܂��B����ʓI�ɂ́C�\���������ς��Ď��̂悤�ɒ�`���܂��B
|
��`�@�@������ԁC���Έʑ� �ʑ���� (S�CU S) ���ʑ���� (X�CU X) �̕�����Ԃł���Ƃ́C�@S �� X�������Ƃł���BU S�����Έʑ��Ƃ����B |
�����ŁC���ӂ��ׂ��́C��̖���̐����ŗp�����C�ʑ� U |S �Ƃ̈Ⴂ�́CS��U ������W���̂��ׂĂł͂Ȃ��CU S �̌���S��U �����Ă���C����ł悢�Ƃ������Ƃł��B
���Ƃ��C
U S���o�ӁC{a}�C{a,b,c} �p�@�i�@���@O |S���o�ӁC{a}�C {a,b}�C {a,c}�C {a,b,c} �p�j
�����ʑ���� �iS�CU S�j �����̒�`�ɏ]���āC (X�CU )�̕�����Ԃł��B�܂�C
U S�@�� U |S�@��U
�̊W�����藧���Ă��āC�ǂ���ʑ���Ԃ����o�����Ƃ��\�ȏW�����ł��B
�m�P�n�@������ԂƓ��l�ɁC�ʑ���ԏ�ɂ��A���ʑ����`���邱�Ƃ��ł��܂��B�������C�ʑ���Ԃɂ͋����Ƃ����T�O���Ȃ����߁h�����h�̔�r�̂悤�Ȃ��Ƃ͂ł��܂���B���̑��苗����Ԃ̘A���ʑ��ɂ����Đ��藧�J�W���̕�܊W�̐����𗘗p���܂��B���̏����Ƃ��āC���̗p����������܂��B
|
��`�@�ߖT�n �i�P�j�@�ʑ���� (X�CU ) ���_ p ���܂ފJ�W�����C�uX �ɂ����� p ���J�ߖT�C�܂��� p ���ߖT�v�Ƃ����CN �܂��� N(p) �Ə����B |
������Ԃł́C�u��-�ߖT�v�ƌĂ�ł������̂ɑΉ����܂��B�ʑ���Ԃł́C�����ɓ�����Â͕s�v�ƂȂ�܂��B�ʑ���Ԃł͊J�W��������p���āC2�̓_ (�v�f)�̋߂���\���̂ł��B
���Ȍ��t���g���āC�ߖT�Ƃ́C�q�����Ă���u���ԁv�Ƃ���������������������܂���Bp�N�̒��Ԃ́C�������̒��ԁC��Ђ̒��ԁC�n��Љ�̒��ԁC�Ƒ��Ȃǂ��낢�날��܂��B�����͂��ꂼ��Cp�N�̋ߖT�ł���C���̂炷�ׂĂ��Z�b�g�ɂ������̂�p�N�̋ߖT�n�Ȃ̂ł��B
�m�Q�n�@���̗p���p����ƈʑ���Ԃɂ�����A�����͎��̂悤�ɒ�`����܂��B
|
��`�@�A�� �i�P�j�@�ʑ���� (X�CU X) ����ʑ���� (Y�CU Y) �ւ̎ʑ� f �� p ��X ���A���ł���Ƃ́C �i�Q�j�@�ʑ���� (Y�CU Y) �̔C�ӂ̊J�W�� UY ��U Y �̋t�����ʑ���� (X�CU X) �̊J�W���ł���C ���Ȃ킿�Cf-1(UY)��U X �ł���Ƃ��C f ���A���ʑ��Ƃ����B |
�i�P�j�C�i�Q�j�ǂ���ł��\���܂���B����͋�����Ԃ̘A���ʑ��ɂ����ėv�������ËߖT V���ip�j�̐��� [#] ���C�ʑ���Ԃł͋ߖT N(p) �̐����Ƃ��� �v���������̂ł��B
�܂��C�A���ʑ��ł��邱�Ƃ͈ʑ���Ԃ��W����p���Ď������Ƃ��ł��܂��B
|
���� �ʑ���� X ����ʑ���� Y �ւ̎ʑ� f ���A���ʑ��ƂȂ�K�v�\�������́C�ʑ����
Y �̔C�ӂ��W���̋t�����ʑ���� X ���W���ƂȂ邱�Ƃł���B |
��
X���oa�Cb�Cc�p�CY�o1�C2�C3�p�C
U X���o�ӁC{a}�C{a,b}�C{a,c}�C{a,b,c}�p
U Y���o�ӁC{1}�C{1,2,3}�p
�Ƃ���B
�ʑ����(X�CU X)����(Y�CU Y)�ւ̎ʑ� f ��
f(x)�� 2�@�@�@�@�ix��a�j 3�@�@�@�@(x��b) 1�@�@�@�@(x��c)
�ƒ�߂�Ƃ��CX�́C
a�_�ł͘A���ł���B
b�_�ł͘A���ł���B
c�_�ł͘A���ł͂Ȃ��B�@
�Ȃ��Ȃ�C
f(a)��2�̋ߖTN(2)�́C{1,2,3}�@�݂̂ł��邪�Ca�̋ߖTN(a)�i��{a}�C{a,b}�C{a,c}�C{a,b,c}�j�̑��͂���{1,2,3}�Ɋ܂܂�Ă���B�����a�_��f�͘A���ł���B
f(b)��3�̋ߖT�͂�͂�{1,2,3}�@�݂̂ł���Ca�_�Ɠ��l�ɍl���āCb�_�ŘA���ł��邱�Ƃ�������B
f(c)��1�̋ߖT�́C{1}�C{1,2,3}�@�Q�ł��邪�C{1}�ɂ��ẮCc�̋ߖT�̑����Cf({a,c})��{1,2}�Cf({a,b,c})��{1,2,3}�ł��邩��C�������{1}�ɂ͊܂܂�Ȃ��B���������āCc�_��
f �͘A���ł͂Ȃ��B
���@�����Ɨǂ���͂Ȃ����H
�m�R�n�@�A�����ƈʑ��̋���Ƃ̊W�ɂ��ďq�ׂĂ����܂��B
�����W���ɑ��ĈقȂ�ʑ��CU �CU �f�iU ��U �f�j����ꂽ�ʑ���Ԃ��iX,U �j�C�iX,U �f�j�Ƃ���Ƃ��C
����
�����ʑ���ԁiX,U �j����ア�ʑ���ԁiX,U �f�j�ւ̍P���ʑ� �͘A�����ƂȂ�B�@ |
��F
���� R �ɋ����ʑ��Ƃ��āC���ׂĂ̊J��Ԃ���Ȃ�W����U �ƁC������ア�ʑ��Ƃ��āC���Cn�Cm��n ��C�ӂ̐����Ƃ���J��� �im,n�j ����Ȃ�W����U �f���l���܂��B���̂Ƃ��C�iR,U �j����ʑ���ԁiR,U �f�j�ւ̍P���ʑ��͘A�����ƂȂ��Ă���B�@
�C�ӂ� f(x) ���܂� N(f(p))��U �f�ɑ��Ă��C���� x ���܂� N(p)��U �����݂��āCf(N(p))��N(f(p)) �Ƃł���B
���Ƃ͊m���߂��܂����CU ��U'�f���t�ɂ���Ɠ��l�ȊW�͐��藧���܂���B�ʑ����A���Ƃ������Ƃ́C��`��̈ʑ����l��̈ʑ���苭���i�ׂ����j���Ƃ������Ă���ƍl���邱�Ƃ��ł��܂��B
�m�S�n�@�ʑ���ԁiX�CU X) ����P�Ȃ�W�� Y �ւ̎ʑ������݂���Ƃ��CY �̕����W����
U Y��{ UY��Y�bf-1(UY)��U X }
���l����ƁCU Y �� Y �̈ʑ��̏����������Ƃ͗e�ՂɊm�F�ł��܂��B����U Y ��U X �����ʑ��Ƃ����C�iY�CU Y �j���iX�CU X) ��������Ƃ����܂��B���̂Ƃ��C
����
�ʑ���� �iX�CU X�j���� ����� �iY�CU Y �j�ւ̎ʑ� �͘A�����ł���B�@ |
�Ƃ������Ƃ��ł��܂��B���ʑ��̒�`����CUY ���J�W���ł���C f-1(UY) �� X �̊J�W���ƂȂ��Ă��邩��ł��B
|
��`�@�����ʑ� |
����͋�����Ԃ̏ꍇ�Ɠ����ł��B
|
���� �i�P�j�@X �̔C�ӂ̊J�W�� UX �̑� f(UX) �� Y �̊J�W���ł���B |
�m�P�n
|
��` X �� U1��U2�@���CU1��U2���� �Ƙa�W������������Ȃ����Ƃł���B�܂��C�A���łȂ��ꍇ����A������Ƃ����CX �̂��ׂĂ̓_�łQ�̘a�W���ɕ����ł���Ƃ������S��A���ł���Ƃ����B �i�Q�j�ʑ���� X �������W�� S ���A���C�܂����A�������W���ł���Ƃ́CS �Ƌ��ʕ���������X �̊J�W�� U1�CU2�ɂ���āC S �� U1��U2�@���CU1��U2��S���� �Ƙa�W������������Ȃ����Ƃł���B�A�������W�����C��W����X�̂P�_�W���݂̂ł���Ƃ��CX �����S��A���Ƃ����B |
����グ�����܂��B
��P�@���[�N���b�h���� (R�COR) �͘A���ł���B
��Q�@�]���Q���t���C���� (R�COs) �͔�A���ł���B�C�ӂ�R�̓_ p �ŁCR��(�|���Cp] �� (p�C��) ��2�̊J�W���̘a�W���ŕ\�����Ƃ��ł���B����āC(R�COs) �͊��S��A���ł���B�@�@�@�@
��R�@ R�̕����W��Q�͔�A���ł���B�Ȃ��Ȃ�CR�̋��ʕ����������Ȃ��Q�̊J�W��(-���C��2)��(��2�C+��)�ɂ����Q�͂Q�ɕ��������B���l��R�̕����W���ł��閳�����S�̂̏W���iR����Q���������W���j��R�Ŕ�A���ł��B
��S�R�@�L���W�� X��{a,b,c} �Ɏ��̈ʑ�O k����ꂽ�ʑ���� (X�CO k) �̘A���C��A���̔���͈ȉ��̂Ƃ���B
| O 1�F�o�ӁC{a}�C{b}�C{c}�C{b,c}�C{c,a}�C{a,b}�C{a,b,c}�p�@ F 1�F�o{a,b,c}�C{b,c}�C{c,a}�C{a,b}�C{a}�C{b}�C{c}�C�Ӂp |
��A���@ �ˁ@�J�W��{a}��{b,c}�Ȃǂ� X ���ł���B |
| O 2�F�o�@�ӁC{a}�C{b}�C {a,b}�C{b,c}�C{a,b,c}�p F 2�F�o{a,b,c}�C{b,c}�C{c,a}�C{c}�C{a}�C�Ӂp |
��A���@ �ˁ@�J�W��{a}��{b,c}�� X���ł���B |
| O 3�F�o�ӁC{a}�C{b}�C{a,b}�C{a,b,c}�p F 3�F�o{a,b,c}�C{b,c}�C{c,a}�C{c}�C�Ӂp |
�A�� |
| O 4�F�o�ӁC{a}�C{a,b}�C{a,c}�C{a,b,c}�p�@ F 4�F�o{a,b,c}�C{b,c}�C{c}�C{b}�C�Ӂ@�p |
�A�� |
|
O 5�F�o�ӁC{a}�C{b,c}�C{a,b,c}�p�@�@ |
��A���@ �ˁ@�J�W��{a}��{b,c}�� X���ł��� |
| O 6�F�o�ӁC{a}�C{a,b}�C{a,b,c}�p�@ F 6�F�o{a,b,c}�C{b,c}�C{c}�C�Ӂp |
�A�� |
| O 7�F�o�ӁC{a}�C{a,b,c}�p�@ F 7�F�o{a,b,c}�C{b,c}�C�Ӂp |
�A�� |
| O 8�F�o�ӁC{a,b}�C{a,b,c}�p�@ F 8�F�o{a,b,c}�C{c}�C�Ӂp |
�A�� |
| O 9�F�o�ӁC{a,b,c}�p�@ F 9�F�o{a,b,c}�C�Ӂp |
�A�� |
�@�@�i���@�J�W��Ok �ɑΉ�����W���̑���Fk �Ƃ��ĕ��L���Ă��܂��B�j
�ȏ�̂悤�ɏW�� X �������ł����Ă��ʑ��̈Ⴂ�ŘA���ł�������C��A���ł������肵�܂��B
�m�Q�n�@�܂��C��̈ꗗ�ɂ́CX�̊J�W���̕�W����X�̕W���ł��邱�Ƃ���CO k�ɑΉ������W������F 8�Ƃ��Ď����Ă��܂��B����������ƁC���̂悤�ɘA�����`���邱�Ƃ��\���Ƃ킩��܂��B
|
�m�A���̒�`�̌��������n �J�W���C���W���ł���W�����ӂ�X�݂̂ł���Ƃ��ʑ���� (X,O )���A���ł���Ƃ����B |
���Ƃ��C�ʑ���� (X�CO 2) �̏ꍇ�C
O2�F�o�@�ӁC �@{a}�C�@ {b}�C {a,b}�C{b,c}�C{a,b,c}�p ���@�ʑ����J�W��
�@�@�@�@���@�@�@���@�@���@�@���@�@���@�@���@�@�@���e�v�f�̕�W���͕W���Ȃ̂�
F 2�F�o{a,b,c}�C{b,c}�C{a,c}�C [c}�C�@{a}�C�@�Ӂ@�p�@�@���@�e�v�f�͕W��
���ꂩ��C�ӂ� X={a,b,c} �ȊO�ɂ� {a}�C��{b,c}���J�W���ł���W���ƂȂ��Ă���̂ŁC
O2�́C�A���ł͂Ȃ��B����A���Ɣ��f����܂��B
�m�R�n �@�A���Ɋւ��邢�����̒藝�ɂ��ďЉ�܂��B
�����ɂ킩�邱�Ƃ͈ʑ���� X �̕������ S1�CS2 �����ꂼ��A���ł����āCS1��S2���ӂȂ�CS1��S2���A���ł���B
�����A���ȏW��S�������Ƃ���W���� {S��}�������ɂ܂Ŋg�����āC
|
�܂�C�A���ȏW���͂����̋�łȂ����ʕ�������āC�h�Ȃ���h���ƂŐV�����A���W��������Ƃ������Ƃł��B
�m�S�n�@�K�������A���łȂ��ʑ���� X �̒��̈�̓_ x1 ���܂ޘA���� X �̕������ S���S�̂̏W�����oS���p�������Ƃ��܂��B����ƁCS���̘a�W�����A����X�̕�����ԂɂȂ�܂����C������C
C(x1)�� S��
�Ə����āC�u x1 ���A�������v�ƌĂԂ��Ƃɂ��܂��B�������C�uC((x1) �� x1 ���܂ލł��傫�ȘA���ȋ�ԁv�ł��B
�����CX ���A���Ȃ�C�C�ӂ� x��X �ɂ��āCC(x)��X �ƂȂ�܂��B
�����łȂ��Ƃ��́CC(x1)�ɑ����Ȃ��_ x2 �����݂��āCC(x1)��C(x2)���ӂƂȂ�܂��B�܂�CX �͏��Ȃ��Ƃ����݂��A���łȂ��Q�̘A���������܂�ł���͂��ł��B
�����āCC(x1)�CC(x2) �̂ǂ���ɂ������Ȃ�x3 ������C���݂��A���łȂ� C(x1)�CC(x2)�CC(x3) �� X �Ɋ܂܂�Ă��邱�ƂɂȂ�܂��B
������J��Ԃ��CX �����݂����ʓ_�̂Ȃ��A�������ɕ�������邱�ƂɂȂ�܂��B
���̕����̂��߂̌J��Ԃ��͗L���̏ꍇ������܂����C������J��Ԃ��K�v������ꍇ������܂��B
�Ⴆ�C������ԂƂ��ėL�����S�̂̏W�� Q ���l�����ꍇ�C�L�����͘A���I�ɑ��݂��Ă��Ȃ��̂Ŋe�L���� q �ɑΉ�����A�������� q ���g��������Ȃ�P�_�W���ł��B�܂�C
�uQ �͉Z�̘A�������ɕ��������v
�̂ł��B������uQ�����S��A������v�ł���Ƃ������܂��B�@�����̌������̂Ƃ��͋�W���ӂ��A�������Ɋ܂߂܂��B�n
�Ȃ��C�u�J���g�[���W���͔�Z�Z�x�������S��A������v�ł��B
�܂��C���ׂĂ̈ʑ���Ԃɂ����āC�u��W����1�_�W���͘A���v�ł���C���S��A����Ԃ��A���ȕ����W���i�A�������j�́C��W����1�_�W���݂̂ł��邱�Ƃ������܂��B
�m�T�n�@�L�����̘b���o�Ă��܂����̂ŁC�ʑ���Ԃł��f���̒�`�������ɏ����Ă����ƁC
|
��`�@�ʑ���ԏ�ł��f���̒�` �ʑ����X �̕����W��S ���CX�̋�łȂ��C�ӂ��J�W��U �ɑ��āC U��S���� �ł���Ȃ�CS��X���f���ł���Ƃ����B ����� S���Z�W���ł���CX �����ł���Ƃ����B |
����R�̕����W��Q�i�L�����j��R�̔C�ӂ̊J�W�� U �� �o (a�Cb) �b a�Cb��R �C-����a��b���� } �ɑ��āC
U��Q���Ӂ@�@�@���@(a�Cb)�@�ɂ͕K���L�������܂܂�Ă���Ƃ�������
�Ȃ̂ŁCQ �� R ���f���ł����C�Ƃ����܂��B
��@�@�]���Q���t���C���� (R�COs) �� Q ���f���ł���B����āC (R�COs) �͉��ł���B
�m�U�n�@�@���̊�{�I�Ȑ����Ƃ��āC
|
���� �i�P�j�@���S��A����Ԃ̕�����ԁA�ϋ�Ԃ͊��S��A���ł���B |
�ؖ���
|
�藝 |
�ؖ���
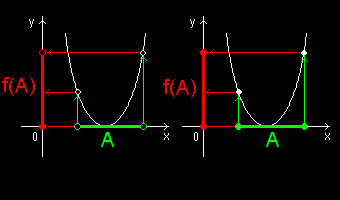
�t�͐��藧�����܂���BA �� Y �̘A���W���ł����Ă� f-1(A) ���A���Ƃ͌���܂���B
 |
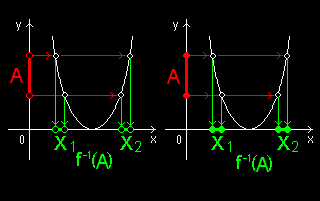 |
��}�͊ȒP�ȗ�ł��B
������ƁC
|
���� |
������ԂɊւ��ẮC
|
���� |
�ؖ���
�m�V�n�@�ʏ�A���ɂ��Ăł��B
�ʏ�A�� �F ������Ԃ̔C�ӂ̂Q�_ x�Cy �ɑ��Ă������n�_�C�I�_�Ƃ���A���Ȑ�������Ƃ��CX ���ʏ�A���ł���Ƃ����܂��B�u�A���v�Ƃ̊W�́C
�ʏ�A���@�@�ˁ@�A���@�@�@�@�@��
�A���@�@�@�@�@�ˁ@�ʏ�A���@�@�~�@�@�A���ȋ�Ԃ��ʏ�A���Ƃ͌���Ȃ�
�ł��邱�Ƃ�������܂��B�A���ȋ�Ԃ��ʏ�A���Ƃ͌���Ȃ���������Ă����ƁC���̋Ȑ�A�ƒ���B�̘a�W���C
A�F�@�@�@����sin�i1/x�j�@�@�@�@�@�@�@�@0��x��1 B�F�@�@�@-1��y��1�@�@�@�@�@�@�@�@�@�@x��0
�͘A�������ʏ�A���ł͂���܂���B�A���ł��邱�Ƃ́CA�̗̈�ł͖��炩�ɘA���ł���C���̕�ł���A��B�͂�����̖���i�Q�j����A���ł��邱�Ƃ�������܂��B
�m�P�n�@�ʑ���Ԃɂ͋����i���j�����݂��Ȃ����ߋ߂��C�����C���邢�́C�������C�傫���Ƃ����T�O������܂���B���̑��ɁC�ߖT�C�J�핢�Ƃ����T�O�����p����C�����̔Z�x�ƕ�܊W���d�v�ƂȂ�܂��B
|
��`�@��{�ߖT�n �ʑ���� X �̓_�@p �̋ߖT�nN (p) [#] �̕����W���� B (p) ���C�C�ӂ� N(p)��N (p) �ɑ��āC |
���̊�{�ߖT�n��p���Ĉʑ���Ԃ��J�W���̔Z�x�Ɋւ����ڂ̉Z���������̂悤�ɒ�`����܂��B
|
��P�Z���� �ʑ���� X�̔C�ӂ̓_ p �ɂ����āC��{�ߖT�nB (p) �����݂��C���̔Z�x�����X�Z�ł���Ƃ��C ���Ƃ���P�Z���������Ƃ����B |
����͓_�ɂ�����J�W���n�̊��̔Z�x���߂Ă��邱�ƂɂȂ�܂��B
�u������ԂȂ�C��P�Z�Z���������B�v�Ƃ����悤�Ȍ�����������܂����C
��P�@�@���ۂɋ�����Ԃ́C
Vn(p)��{ x��X�bd (p�Cx)��1/n }
�Ƃ���C�C�ӂ� N(p) �ɑ��ď\���傫�� n ��I�ׂCVn(p)��N(p) �Ƃł���̂ŁCV ��{ V1(p), V2(p), �c�@} �͊�{�ߖT�n�ƂȂ�܂��B
��Q�@�@�]���Q���t���C���� [#] �͑�P�Z���������Bp �̊�{�ߖT�n�́C�Ⴆ�C
V��{ (p�|1/n�Cp]�bp��X�Cn��1�C2�C�c�@}�@
�̂悤�Ɏ�邱�Ƃ��ł��܂��B
�m�Q�n�@�ȏ�� X �̓_�ɂ��Ăł������C���x�͕����W���ɂ��Ă̓��l�ȕ����J�W�������l���܂��B
|
��`�@�J�� �i���̂P�j �i�P�j�@�ʑ���� X �̕����J�W���� B ���o B�� �p�������@��p���āCX �������W�� S ���C�iS��X �ł��悢�j
�ƕ\����Ƃ��CB �� S ���J�핢�Ƃ����B���ɁC �h����1�C2�C3�C�c�h �̂Ƃ����Z�J�핢�C �h����1�C2�C����Cn �h�̂Ƃ����L���J�핢�Ƃ����B �i�Q�j�@�܂��CX ���C�ӂ̊J�W��U �ɑ��āC X �̕����J�W����B ���o B�� �p������ ����ꕔ���o B���f �p���f�����f�����o���āC
�ƕ\����Ƃ��CB ���ʑ���� X ���J���Ƃ����B�@���ɁC �h����1�C2�C3�C�c�h �̂Ƃ����Z���Ƃ����B |
�����ŁC�Y�������͔�Z�W���ł��\���܂���B�Ⴆ�C��ԁ@(0�C1) �̎����Ȃǂł��ǂ��킯�ł��B
�m�R�n�@�Ⴆ�CX ����� (0�C1)�@�i��R�Ɠ����j�Ƃ���Ƃ��C
�i �� �j �J�W�����Ƃ��āC{ (1/n�C1�|1/n)�bn��3�C4�C�c }�@�Ƃ���ƁC�����X�̉Z�J�핢�ł��B
�i�A�j �J�W�����Ƃ��āC�o (0�C1/2)�C(1/3�C1) �p�Ƃ���C�����X�̗L���J�핢�ł��B
�i�������j �J�W�����Ƃ��āC{ (0�Ca)�ba��(0�C1) }��{ (a�C1)�ba��(0�C1) } �Ƃ���C��Z�Z�x�̊J�핢�ł��B
�ȏ�̏W�����͊J�핢�ł͂����Ă��J��ł͂���܂��C
(iv)�@�J�W�����Ƃ��āC B��{ (qm�Cqn)�b0��qm��qn��1�Cqm�Cqn ��Q }
���l����ƁC����� X�� (0�C1) �̉Z��ƂȂ�܂��B
��̈ʑ���Ԃɑ��āC�l�X�ȊJ�핢���l������̂ł����C�ʑ��̋����C�ア�ɑ�������悤�Ȏ��̗p�ꂪ�g���܂��B
|
��`�@�@�ו� �ʑ���� X �̊J�핢 U ��V �ɂ��āAV ��U ���ו��ł����Ƃ́A�C�ӂ� V��V �ɂ��� U��U �����݂��� V��U �������Ƃ������B |
�m�S�n�@�J��̕ʂ̒�`�Ƃ��āC
| ��`�@�J��i���̂Q�j �C�ӂ� p��X �̔C�ӂ̋ߖT N���m �ɑ��āCp��B��N�@�ƂȂ�悤�� X �̕����W����B �̌��i�W���jB �����݂���Ƃ�B �� X ���J���Ƃ����B |
�Ƃ����̂��ؖ��ɂ悭�g���܂��B��قǂ̊J�W���� (iv)B��{ (qm�Cqn)�b0��qm��qn��1�Cqm��Q�Cqn��Q } ���Ƃ�C (0�C1)�̔C�ӂ̋ߖT (s�Ct) �ɑ��āCs��qm��p��qn��t �ƂȂ�悤�� (qm�Cqn)��I��ŁC�i���̂Q�j���������܂��B�������C����B �̗v�f�͉Z�Ȃ̂ŁCB ���Z���ƂȂ��Ă��܂��B
��P�@�@�P�������[�N���b�h��Ԃ͉Z������BB��{ (qm�Cqn)�b-����qm��qn��+���Cqm��Q�Cqn��Q } �Ƃ���悢�B
|
��`�@��Q�Z���� �ʑ���� X ���Z�������Ƃ��C�ʑ����X����Q�Z���������Ƃ����B |
�P�ɁC�u�ʑ���� X ���Z�������v�Ƃ����悤�Ɉ��p���邱�Ƃ������ł��B
�m�T�n
��@�@�]���Q���t���C�����͑�Q�Z���������Ȃ��B
�]���Q���t���C���� (R�COs) ���Z��B �����Ɖ��肵�Ė������B
�C�ӂ� p��R �C(p�|1�Cp] ��Os �ɑ��āC
p��Bp��(p�|1�Cp] �@�@�������ŁCp�̉E���h ] �h �ł��邱�Ƃ������Ă���I
�����CBp��B�@�����Ȃ��Ƃ���͑��݂���B�i�����Z�����̒�`�i�Q�j����j
�����ŁCR ���`��Ƃ���ʑ� f �F
p�@���@Bp
���l����ƁC�������Z�Z�x��������R�����Z�Z�x�̏W����v�f�Ƃ��镔���W����B �ւ̒P�˂ƂȂ薵������B
����āC�]���Q���t���C���� (R�COs) ���Z��������Ȃ��B
�Ȃ��Cf ���P�˂ł��邱�Ƃ́C���̂悤�ɔw���@�ŏؖ��ł���B���Ȃ킿�C
�����C�P�˂ł͂Ȃ���C ���� p��Bp�Cq��Bq �i p��q ) �����݂��āCBp��Bq �ƂȂ�B�Ƃ��낪�C��ʐ����������ƂȂ� p��q �Ƃ���C
q(p�|1�Cp]�@�Ȃ̂ŁCq
Bp�@(��Bq )�@�������ł��Cp�̉E���h ] �h �ł��邱�Ƃ������Ă���I
�ł��邱�ƂƂȂ�C��������B����āCf �͒P�˂ł���B
�m�U�n
|
�藝 |
���̒藝����C
��P�@���ł���C�ʏ�̎����̈ʑ����瓱����鋗�������������͑�Q�Z���������B
��Q�@��Q�Z���������Ȃ����ȃ]���Q���t���C���� (R�COs) �͋�����Ԃł͂Ȃ��B
�܂�C��������(R�COs) ��ɒ�`���邱�Ƃ��s�\�Ȃ��Ƃ�������܂��B
�m�P�n�@�L���핢�Ƃ����p���p���āC���̂悤�Ɉʑ���Ԃɂ�����u�R���p�N�g�v�̒�`���Ȍ��ɏq�ׂ邱�Ƃ��ł��܂��B
|
��`�@�@�R���p�N�g |
X ����ł��L�������핢���܂܂Ȃ��J�핢������CX �̓R���p�N�g�ł͂���܂���B�������CX�̗L�������핢����Ꭶ��������Ƃ����āCX ���R���p�N�g�Ƃ������Ƃ͂ł��܂���B
���������āC�R���p�N�g�łȂ����Ƃ��ؖ�������C�R���p�N�g�ł��邱�Ƃ�����������ʓI�ɓ���킯�ł��B
����R�̋�� X��(0�C1) �͉Z�̊J�W���ŁC
X�� �� (1/���C1) ����2�C3�C�c
�ƊJ�핢����܂����C����͗L�������J�핢���܂݂܂���B�i���͕K�����܂łƂ�K�v������j�B����āC�����̋��(0�C1) �̓R���p�N�g�ł͂���܂���B
����C�ʑ���ԂƂ��āC
�u������̕�� X���m0�C1�n �̓R���p�N�g�v
�Ƃ������Ƃ��ł��܂��B�i�ǂ�����ďؖ����܂����H������ł��傤�H�j
�m�Q�n�@���̂��߂ɂ͎��̒藝���K�v�ƂȂ�܂��B
|
�n�C�l�E�{�����̔핢�藝 Rn�̗L�E�W�����J�핢�ł���Ȃ�C��������I�L���̊J�W����p���ėL�E�W����L���J�핢�ł���B |
���̒藝��������̗L�E��ԂɌ��肵���i�ؖ����₷���悤�ȕ\�L�Łj�q�ׂ�ƁC
|
��� F0��[a�Cb] �̔C�ӂ̉Z�J�핢��B �� { B1, B2�C �c } �Ƃ���ƁC
�ƕ\����B���̂Ƃ��CB ����L���̊J�W�� �oB01�C����CB0n �p��I��ŁC [a�Cb] �� B01�������B0n �Ƃ��邱�Ƃ��ł���B �������Z�J�핢�������Ƃ͂��łɏq�ׂĂ��܂�[#]�B |
�m�R�n�@�ȏ��w���@�ŏؖ����邽�߂ɁC
�u�@�@�`�@�@�CB ����ǂ�ȗL���́oB01�C����CB0n �p��I��ł��C
[a�Cb] �� B01�������B0n
�Ƃ��邱�Ƃ��ł��Ȃ��B�v
���������āC�����т��܂��傤�B
�ؖ�
�܂��C��� [a,b] ���Q�������āC[a,c] �� [c,b] �Ƃ���B
��� [a,b] ��B ����I�L���̊J�W���ł͔핢�ł��Ȃ��Ƃ���ƁC�Q�������[a,c] �� [c,b] �̂����ŏ��Ȃ��Ƃ��ǂ��炩�����B ����I�L���̊J�W���ł͔핢�ł��Ȃ��B
[a,c] �� [c,b] �̂����ŗL���핢�ł��Ȃ����� F1 = [a1�Cb1] �Ƃ���B
�������C[a,c] �� [c,b] �̗����Ƃ��L���핢�s�\�Ȃ�C�ǂ����I��ł��悢�B
����ɁC[a1�Cb1] ��c1�łQ�������ĂQ�̕�� [a1�Cc1]�C[c1�Cb1] ���l����ƁC�ĂсC���Ȃ��Ƃ��ǂ��炩�����B ����I�L���̊J�W���ł͔핢�ł��Ȃ��B
�����ŁC�L���핢�ł��Ȃ������@F2 = [a2�Cb2] �Ƃ���B
������J��Ԃ��ƁC
F �� F1 �� F2 �� �E�E�E
�ƂȂ��Ԃ̗����邱�Ƃ��ł���B�������C��Ԃ̕��́C�bFk�b���bbk-ak�b��(1/2)k�bb�|a�b �Ȃ̂ŁC
�bFk�b��0�@�@�@�@�@�@�@�@�@[**]
�ƂȂ�B
�����āC�����̘A�����i��ԏk���@�j���C�Ɍ��ɂ����Ď��� p0��[a,b] �����݂���B
�i���ӁF�J��ԁia�Cb�j�œ��l�ȍl�@������ƁC�Ɍ��Łia�Cb�j�̋��E�ւ͂ݏo���\�������邪�C��Ԃł͂��̐S�z���Ȃ��B�j
[*] ���Cp0 �� Bn �ƂȂ� Bn �����݂��C����ɁCBn �͊J�W���i�J��ԁj�Ȃ̂ŁC����J�W�� V(p0) �����݂��āC
V(p0) �� Bn
�Ƃ��邱�Ƃ��ł���B�܂��C[**]���C�\���傫�Ȑ��� k ���Ƃ�ƁC [ak�Cbk] �͂�����ł��k���ł��āC
p0 �� [ak�Cbk] �� V(p0) �� Bn
�Ƃ��邱�Ƃ��ł���B
�Ƃ��낪�C�Ō�̊W���́CB ����I�L���̊J�W���ł͔핢�ł��Ȃ��悤�ɑI�͂��� [ak�Cbk] ��B �̈�̊J�W��Bn �ɂ���Ĕ핢����Ă��邱�Ƃ������Ă���C�����������Ă���B
���������āC�w���@�ɂ��ŏ��̉���͔ے肳��C
�uB ����K���ȗL���� { B01�C����CB0n} ��I�ׂC
[a�Cb] �� B01�������B0n
�Ƃ��邱�Ƃ��ł���B�v
���Ƃ��ؖ�����܂����B
��
�]���Q���t���C���� (R�COs) �̓R���p�N�g�ł͂Ȃ��B
OR �� Os�@�@��(R�COR )���R���p�N�g�łȂ�����B
�m�S�n�@�R���p�N�g��Ԃ̊�{�I�Ȑ����ɂ͎��̂悤�Ȃ��̂�����܂��B
| ����
�i�P�j�@�ʑ���� X �ƈʑ���� Y ���ʑ����^�ł���Ƃ��CX ���R���p�N�g��ԂȂ�CY ���R���p�N�g��Ԃł���B �i�Q�j�@�R���p�N�g��Ԃ̔C�ӂ̕W���̓R���p�N�g�ł���B �i�R�j�@�ʑ���� X ����ʑ���� Y �ւ̘A���ʑ� f �ɂ���Ĉڂ����CX �̃R���p�N�g�W�� A �̑� f (A) �́CY �̃R���p�N�g�W���ł���B �i�S�j�@�R���p�N�g��Ԃ̔C�ӔZ�x�̒��ς́C�R���p�N�g��ԂƂȂ�i�`�R�m�t�̒藝�j�B |
�ʑ��I�Ȑ���
�i�P�j�̐������C�R���p�N�g�Ƃ͈ʑ��I�Ȑ����ł���Ƃ����܂��B����ŁC�W���C�L�E�W���Ƃ����͈̂ʑ��I�Ȑ����ł�����܂����B
����
| - | �]���Q���t���C ���� |
���[�N���b�h�@ ���� |
| �ʑ� | Os�@�@�@ ���@�@�@OR | |
| �� �F Q��R���f�� | �� | �� |
| �R���p�N�g | �~ | �~ |
| �Z�R���p�N�g | �~ | �~ |
| �ЃR���p�N�g | �~ | �� |
| �Ǐ��R���p�N�g | �~ | �� |
| �p���R���p�N�g | �� | �� |
| �����f���[�t | �� | �� |
| �A���� | ���S��A�� | �ʏ�A�� |
| ��P�Z���� | �� | �� |
| ��Q�Z���� | �~ | �� |
| �n�E�X�h���t | �� | �� |
| ���� | �� | �� |
| ���K | �� | �� |
| �������\ | �~ | �� |
|
��` U����V�ւ̑S�P�� f �Ƃ��̋t�ʑ� f-1 ���Ƃ���Cr���ʑ��ł���Ƃ��Cf ��Cr�����������ʑ��Ƃ����B ���̂Ƃ��CU �� V ��Cr�����������ł���Ƃ����B |