| Appendix 3 距離空間 | |
| f-denshi.com [目次へ] 最終更新日: 2014/6/21 追記しました(仮)。 | |
| サイト検索 | |
ルベーグの偉業は,”長さ” の概念の変革ということができます。もちろん,これだけでも価値のあることですが,ルベーグ積分が20世紀の数学の不可欠な道具として位置づけられた理由は,この概念の適用範囲がユークリッド空間の ”長さ” にとどまらず,これから述べる距離空間と呼ばれる集合の抽象化された長さ=”距離” に適用されていったからです。抽象とはいっても,工学的な応用において重要なフーリエ変換や量子力学の基礎理論であるヒルベルト空間論の屋台骨となっているので,数学者だけなく,物理学者やエンジニア等多くの人々の関心惹きつけていきました。「The講義」においてもルベーグ積分をディリクレ関数の積分で終わらせてはもったいないので,距離空間について話を進めていくことにします。
[1] ユークリッド幾何学において,”2点の間に1本だけひくことができる線分の長さ” のもつ性質から次のようなエッセンスを抽出した(2つの点から”線分(実数値)”への)写像を距離と呼び,集合の任意の2つの点(元)に対して距離が定義可能な集合を距離空間(metric space,distance space)と呼びます。もちろん,普通のユークリッド空間は距離空間のもっとも典型的な例です。
|
距離空間の定義: 集合 X の任意の2つの元 x,y から実数 d への写像 d(x,y) : d(x,y): x,y → d が与えられて, (1) d(x,y)≧0 を満たすとき,d(x,y)を距離,集合 X を距離空間 (X,d)という。 |
ここで,(3)はユークリッド幾何学における「三角形の2辺の長さの和は他の1辺の長さより長い」ということに基づいていることは言うまでもありません。距離空間は話の流れから d が自明な場合は ” 距離空間 X ” と書かれることもあります。
[2] 3次元ユークリッド空間はもちろん,距離空間であって,
集合 X ⇒ R3={r | r =(r1,r2,r3); r1,r2,r3∈R } ← r∈R3 とも書いてもよい
の任意の2つの元 x =(x1,x2,x3),y =(y1,y2,y3)について写像,
| 距離 d2≡d2(x,y)= | |x1−y1|2+|x2−y2|2+|x3−y3|2 | [ユークリッド空間の距離 d2] |
を導入したものです。
他にどのような写像がRn,Cn に導入可能な距離となり得るか,例を挙げておくと次のようになります。
| 距離空間 X |
距離 d の定義 |
||||||||||
|
(1) 離散距離空間 |
|
||||||||||
| (2) (Rn,dp) |
|
||||||||||
| (2)’ (Rn,d∞) |
|
||||||||||
| (3) (x1,・・,xk,・・)∈R∞ (R∞,d) |
|
||||||||||
| (4) n次元ユニタリ空間 (Cn,d2) |
|
* 念のために注意しておくと,ただ,距離空間 というときには集合の元の間にいわゆる内積が定義されている必要はありません。
[3] 距離空間を作りだせる集合として,ユークリッド空間,ユニタリ空間以外の重要な例としては,” 関数の集合 ”となります。その場合に距離として導入される写像とは,2つの関数に対して1つの実数が対応するような関数を定義域とする写像,すなわち汎関数です。具体的な例を挙げておくと次のようになります。
| 距離空間 X |
距離 d の定義 |
||||
| (5) 閉区間[a,b]上の連続関数:C[a,b] (C[a,b],d∞(f,g)) |
d∞(f,g)=Max|f(x)−g(x)| ; a≦x≦b | ||||
| (6) 閉区間[a,b]上の連続関数:C[a,b] (C~[a,b],d1(f,g)) |
|
(関数を元とする集合に)距離を導入することを,「位相を入れる」というような言い方をします。(5)で定義される距離は,初等解析学で「一様収束」なるものを考えるときに使いましたね。覚えてますか⇒[#]
[1] ユークリッド空間上で展開される初等解析学で学んだ距離,すなわち,距離d2 が関与するいくつかの定義を,
距離 d2 → d (=ここで定義された一般化された距離)
とすることで,距離空間 (X,d) における定義として用いることができます。 例を挙げておきます。
距離空間 (X,d) が与えられ,その部分集合を S,O,F (∈X) とするとき,
| 用語 | 記号 | 定義 | ||||
| ε-近傍 | Vε(x) |
x∈X と正数εに対して, { y | d(x,y)<ε } |
||||
| 境界点 | p,∂ | Xのε-近傍がSに属する点と属さない点の両方を含む点 x ∈X (境界点全体の集合を境界といい,∂S のように書く。) |
||||
| 内点 | x | x∈Sで,十分小さなεを選べば,Vε(x)⊂S である。 | ||||
| 集積点 | a | S から適当な相異なる無限点列 { x1,x2,・・・,xn,・・・ } を取り出したとき, これが n→∞ で収束する点 a ( つまり,n→∞ で d(xn,a)→0 となる点 a。) |
||||
| 閉包 |
|
S と S のすべての集積点との和集合。 | ||||
| 開集合 | O | 任意の点 x∈O について十分小さなεを選べば,Vε(x)⊂O である。 (=内点だけからなる集合,つまり,∂O∩O=φ) |
||||
| 閉集合 | F | F の任意の集積点が必ず F に属する。 または,Fの境界が必ずFに含まれる。(つまり,∂F⊆F ) |
これらの用語はユークリッド空間に対して使われる場合[#]を理解していればとりあえず,問題ありません。
開集合と閉集合は相反する概念ではありません。つまり,
(1)閉集合でも開集合でもない集合がある。
(2)閉集合であり,かつ,開集合である集合がある。
例を挙げておくと,(1)はRの半開区間,(0,1] などですが,(2)の例としては,
例:有理数の全体を距離空間 X=Q とするとき,その部分集合 S={ q∈Q:q2<2 } は,Qの開集合であり,Qの閉集合でもある。
この例はXとして,Qを考えるのでなく,実数とすれば,X=Rの開集合となります
[2] 集積点 a は S に含まれていることも S に含まれないこともあるのはユークリッド空間の場合と同様ですが,閉包,閉集合に関しては,次の定理が重要です。
| 定理: S の閉包 [S] は S を含む最小の閉集合である。 |
[3] 次にコンパクトという用語ですが,ユークリッド空間上の初等解析学ではコンパクトは有界な閉集合という意味でしかありませんでしたが,距離空間においては,次のような定義がそのまま意味をもつので,そのまま解釈する必要があります。
|
定義: |
定義から,有界であっても開区間(-1,1)はコンパクトでないことはすぐにわかります。この開区間は,例えば,連続関数 y=tan(πx/2) を用いて,とてつもなく大きい区間(−∞,∞)に全単射で対応させることができますので,文字どおりコンパクトではないのです。
日常生活でも「コンパクトなサイズ」というような言い方をしますが,数学では単に有限の範囲に収まるというだけでなく,全単射連続写像を用いて無限に引き伸ばすことが不可能なときに初めてコンパクトと呼ぶことができるのです。
「コンパクト」が初等解析学における「有界閉集合」の単なる言い換えではないというもう一つの例を次に挙げておきましょう。
正確に言うと,次に述べる集合は,ヒルベルト空間 (←後で,正確な定義を述べます⇒[#])と呼ばれるものですが,ここでは無限次元のユニタリ空間 [#] くらいに考えて読んでください。
無限次元の複素数を成分とする無限次元のベクトル,
C∞={z =(z1,z2,・・・) | zk∈C }
の部分空間である単位球面:
SH ={z | |z |=1} ( ← 半径=1 )
の集合を考えます。ここで,SH の元,z,w との距離は,ユークリッド空間の場合の自然な拡張として,
(4) d(z,w)= |z1−w1|2+|z2−w2|2+ ・・・
で定義することとします。 すると,SH が閉集合(集積点はSH 内にある)であり,
(1) 任意の z,w ∈SH について, d(z,w)≦2 (←直径) ,つまり,SH は有界閉集合である。
ことが分かります。一方,SH の部分集合として, C∞ の基底ei からなる無限集合を考えるとその中から異なるものを取り出してつくった無限列は,
||ej−ek||= 2 ; j ≠ k
であることから,決して収束しません。(収束するならば,||ej−ek||→0 (コーシー列)でないとだめ) つまり,この無限列は集積点をもちません。すなわち,
(2) SH はコンパクトではない。
といことになります。このような事態に陥った原因は,もちろんベクトルを無限次元としたからです。無限とはやはりいろいろと厄介者なんです。
以下,追加 (2014/6/21)
[4] 距離空間の閉集合と開集合の定義を少し表現を変えてもう一度書くと,
|
定義 距離空間の閉集合と開集合 Vε(x)⊆O が成り立つことである。 距離空間(X,d)の部分集合FがXの閉集合であるとは,任意の点 x∈Fc に対して,ある正数εが存在して, Vε(x)∩F=φ が成り立つことである。ただし,Fc≡X−F [Fの補集合] |
定義から,O が X の開集合であるならば,補集合 Oc はXの閉集合であり,F が X の閉集合であるならば,補集合 Fc は X の開集合であることもわかります。
閉集合と開集合は相反する概念ではありません。例えば,下図に示されたようなR2の部分空間 X=A∪B を考えると,AはXの開集合とXの閉集合の両方の定義を満たしていることが分かります。
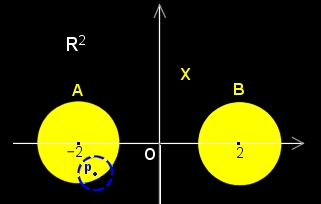 |
XはR2の部分集合で,X=A∪B ただし, A=((x,y)|(x+2)2+y2≦1) B=((x,y)|(x−2)2+y2≦1) とする。 このとき,R2,またはXの部分集合Aについて, (1)AのR2に対する境界はAの円周であるが, (2)AのXに対する境界はφである。 (3)AはR2の閉集合であるが, (4)AはXの開集合であり,閉集合でもある。 (Aの任意の点xのVε(x)はεが十分小さければ, XのAc (=B)へはみ出さないので開集合ですが, 一方,任意のy∈Ac (=B) について,εが十分小さければ, Vε(y)∩A=φであるからAはXの閉集合です。) |
* 境界,開集合,閉集合は相対的なもので,どの集合に対するものかで違ってくることに注意が必要です。
もう一つ例を示しておきます。
例: 距離空間 X={ x∈R:0≦x<2 } の部分集合
A={x∈R:0≦x<1}
B={x∈R:1≦x<2}
を考えると,AはXの開集合であり,BはXの閉集合である。
(なお,A,BともにRの閉集合でもRの開集合でもない。)
[5] 距離空間の開集合,閉集合に関しては次のことが確かめられます。
|
開集合,閉集合の性質 (X,d)の開集合,O1,O2,O3,・・・,空集合φ,X自身について次の集合はいずれもXの開集合である。 (O1) X,および,φ (X,d)の閉集合,F1,F2,F3,・・・について,空集合φ,X自身について次の集合はいずれもXの閉集合である。 (F1) X,および,φ |
(O3)で有限個の条件を外すことはできません。たとえば,Rの部分集合,
On=(−1/n,1/n)
n∈N(自然数)を考え,この可算無限個の共通分の集合を考えると,
On = {0} ←点0からなる集合
となりますが,{0}は開集合ではありません。しかし,有限個に止めておけば, O1∩O2∩O3=(-1/3,1/3) は開区間で開集合です。
(F2)で無限濃度の和集合について,例えば,
Fn=[-1+1/n,1−1/n]
を考えると,有限個に止めておけば, F1∪F2∪F3=[-2/3,2/3] で閉区間ですが,無限に和をとれば,
Fn =(-1,1)
となり,これは閉区間ではなくなり,開区間です。
上の性質は距離空間で定義された開集合,閉集合から導かれた性質ですが,距離空間が背景にあったことを完全に忘れてしまって,上に示した(O1),(O2),(O3)を満たすような集合Oj の集合(=位相と呼ばれる部分集合族 [#])を改めて公理として含むような空間を考えることができます。そのような空間は位相空間と呼ばれます。位相空間についてはこちら⇒[#] を参考にしてください。
[6] 余談ですが,開区間は可算個の半開区間の和でも表せます。
(0,1)=
1− 1 ,1− 1 n n+1
[1] ユークリッド空間での連続写像と同様に,距離空間における連続写像を次のように定義します。
|
定義 連続写像 距離空間(X,d)から距離空間(X’,d’)への写像 f(x) ,x∈X が,xで連続写像であるとは, 任意の正数εに対して,あるδが存在して, (1) f(Vδ(x) )⊆ Vε(f(x)) が成り立つことである。 (Vε(x):ε近傍 [#] ) また,すべてのXの点で連続であるときは,f(x)はXで連続写像であるという。 (2) d(x,y)<δ ⇒ d’(f(x),f(y))<ε が成り立つ。 |
連続写像であることの別の表現は,任意の点列 xn について,
xn→x ならば,f(xn)→f(x)
であることを示しても構いません。
[2] また,定義域と値域の距離関数 d とd’とは異なっても構いません。ユークリッド空間上の初等解析学では距離はd2だけなので,連続写像であるかどうかは一意的でしたが,一般的な距離空間では,同じ集合Xであっても,距離関数によって連続であったり,不続連続であったりというこも起こり得ます。
例: 恒等写像 f(x)=x : (R,d2)⇒(R,d2) は連続写像であるが,像の距離関数を離散距離関数d0 [#] とした,
恒等写像f(x)=x : (R,d2)⇒(R,d0)は至るところ不連続である。(どんなにxをx0に近づけて,d2(x−x0)→0 としても,d(f(x)−f(x0))=1 (x≠x0)であり,決して0に近づかないからです。)
逆に,同じ距離関数であっても集合 X が違えば,連続性が変わってくることもあります。
例: 距離空間 (Q,d2) 上で定義された関数 f (x): x∈Q ⇒ {0,1}
f(x)= 0 (x<√2) 1 (x>√2)
はQ (有理数)上の連続関数である。もし,f(x)が距離空間 (R,d2) 上で定義された関数 x∈R ⇒ {0,1}であるならば,f(√2)の値を 0 か 1 に対応させてやらなければなりませんが,どちらに定めようともこの点で関数は連続とはなりません。
[3] 距離空間における連続写像の性質は次のように開集合,閉集合を用いて表すことができます。
|
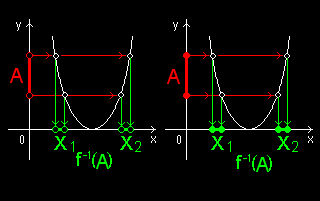
定理 連続写像と開集合・閉集合との関係 距離空間(X,d)から距離空間(Y,d’)への写像 f(x)∈Y ,x∈X が連続写像であることは,次の2つと同値である。 (1) Yの任意の開集合Oに対して,f-1(O)はXの開集合である。 |
証明 「f(x)が連続写像」 ⇒ (1) は,下図を参考にして,
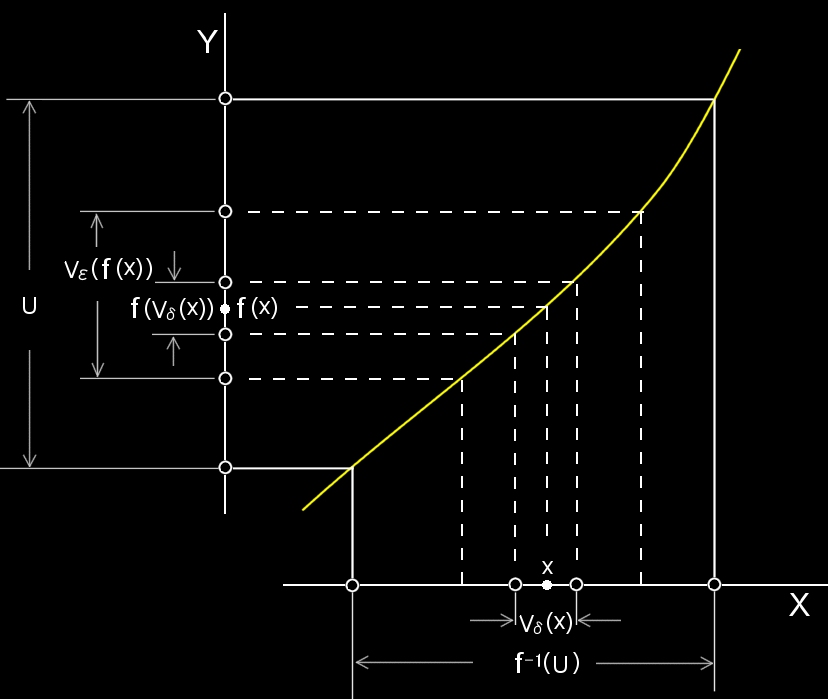
任意のY の開集合Uに対応する f-1(U) における任意の点x の像 f(x) の近傍Vε(f(x)) に対して,あるδ>0 が存在して,
f(Vδ(x)) ⊆ Vε(f(x)) ⊆ U ←連続写像の定義 [#] & 開集合の定義
とすることができる。すなわち,(上式の両端を見て)
Vδ(x)⊆f-1(U) ⇔ f-1(U) は X の開集合 ←開集合の定義は ⇒ [#] をみよ。
(1)⇒「f(x)が連続写像」(上の説明を逆に辿る)
(2)の証明は演習問題 (2)はほとんど使われない。
 |
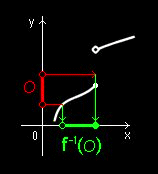 |
距離空間では,これは定理として得られますが,後述の位相空間{#]においては,連続写像の定義として(1),(2)の開集合の性質がそのまま用いられます。
|
定義 開集合系 距離空間(X,d) のすべての開集合からなる集合族は開集合系と呼ばれ,τ(X,d),または,τ(d) と表される。 |
一般に,τ(X,d)⊂β(X) (Xのべき集合)ですが,X が Z (整数)の場合や,離散距離空間 (X,d0) では,τ(X,d)=β(X) となります。
そのような場合,X のべき集合β(X)を離散位相と呼びます。
一般に,同じ集合に対しても距離が異なれば,開集合系も異なりますが,τ(X,d )⊂τ(X,d' )であるとき,前者を弱い位相,後者を強い位相といいます。もっとも強い位相は離散位相となります。
例 距離空間 (Rm,d2) の連結な部分集合 O に含まれる点 p について,あるε>0 をとると Vε(p)⊂O
とできるとき,O はRm の開集合であるが,このようなRm の開集合全体からなる開集合系をOR と書き,Rmの自然な位相という。 ( τ(Rn,d2)≡OR ということ。)
例 τ(Rn,d2)=τ(Rn,d1)=τ(Rn,d∞) である。
さらに詳しいことは位相空間のところで説明します。 ⇒ [#]
[1] 連続写像を用いて,同相写像が次のように定義されます。
|
定義 同相写像 同相を位相同型と言うこともあります。 |
これはトポロジー(幾何学)では,図形の連続的に互いに移り変われる”変形”を厳密に定義するために使われます。
例1: 距離空間(I,d)と(R,d)は同相写像 y=tan(πx/2),y∈I,x∈R によって同相。ただし,Rは実数全体,I は開区間(-1,1),距離関数 d(x,y)=|x−y|
例2: 距離空間(Rn,d2)と(Rn,d1)と(Rn,d∞)は同相,ただし,
d2(x,y)= |x1−y1|2+|x2−y2|2+・・・+|xn−yn|2
d1(x,y)=|x1−y1|+|x2−y2|+・・・+|xn−yn|
d∞(x,y)= max
1≦k≦n|xk−yk|
ここでは,恒等写像: f(x)=x が同相写像となっている。
例3 同相写像でない例:
距離空間 (C(I),d∞) から距離空間 (C(I),d1) への恒等写像f を考えると,f は連続写像であるが,逆写像 f-1 は連続ではない。
例4: ユークリッド (R,d2) の部分空間 (Q,d2) と (Z,d2) との間に同相写像は存在しない(証明略)。 つまり,ZとQの濃度は等しいが,同相ではない。
[2] 同相写像の性質
|
同相写像 X→Y で移り合う性質(やや,あいまいな言い方だが): (1) xn → p ⇔ f(xn) → f(p) (2) V が X の点 x の近傍 ⇔ f(V) は Y の点 f(x) の近傍 (3) O が X の開集合 ⇔ f(O) は Y の開集合 (4) F が X の閉集合 ⇔ f(F) は Y の閉集合 (5) [S] が X の閉包 ⇔ f([S]) は Y の閉包 |
もう一つ。
|
距離空間 (X,d) と (X,d’) が同相ならば,それらの開集合系は等しい。τ(X,d)=τ(X,d’) |
結局,同じ開集合系を持つ空間が同相であることから,(必ずしも距離d が定義されていない)開集合系τ[#] を集合 X に付与した空間を,同相写像によって不変の性質をもつ空間として,位相空間 (X,τ) を定義することができます(位相空間論)。この場合,位相(または位相構造)とは開集合系のことで,また,開集合は公理として,先の(O1),(O2),(O3)を満たす X の部分集合[#] と定義されます。
例 位相空間としては,(Rn,τ(Rn,d2))=(Rn,τ(Rn,d1))=(Rn,τ(Rn,d∞)) である。
位相空間では距離が定義されないため,近さ(距離の大小)の概念がほとんどありません。”ほとんど”と述べた理由は,距離が無限大の状況は位相空間ではコンパクトという概念で区別されるからです。
位相空間では同相な空間は区別しないということなので,一次元ユークリッド空間では有界な開区間 (-1,1) も位相空間では無限空間 (−∞,∞)と同じとみなされます。つまり,位相空間では距離に相当するものは,伸び縮みの自由度が無限であるか有限 ( =コンパクトであるか否か) の2通りしかありません。詳しくは「Appendix1位相空間」,「Appendix2位相空間」のところで説明します。
最後に定理を一つ紹介します。
| 定理 任意の距離空間は2点間の距離が常に1以下であるような適当な距離空間と同相である。 |