| Appendix 6�@�@�ʑ���ԂQ�@�������� | |
| f-denshi.com �@�m�ڎ��ցn�@�@�ŏI�X�V���F�@�@�Z�����@�@�@ | |
| �T�C�g���� | |
�m�P�n�@������ԂƂ��̕����W���ɂ��Đ��藧���ʂ̃G�b�Z���X�̈���u �W�� X �ƊJ�W����O �v�Ƃ����`�Ŏ��o���Ĉʑ���ԂƂ����T�O���u�ݒ�v���Ă��܂��B���̉ߒ��ł́C������ԂŐ������鑼�̐��������O���ꂽ���ߋ�����Ԃł͂��肦�Ȃ��悤�Ȑ���������Ԃ��ʑ���ԂɊ܂܂�邱�Ƃ��������Ă��܂��B
���̈ʑ���ԂƋ�����Ԃ̌��Ԃ̕����́C�������̈ʑ��ɑ��ĕt�����������������p���ĕ��ށE�c�_����܂��B
���ɁC�ʑ��ɂǂ̗l�ȏ��� (����) ���ʑ���Ԃɕt�^���������ԂɂȂ�̂ł��傤���B���̖��ɂ��Ĉ�̓�����^�����̂��E���]�[���ł��B���̓����͎��̒藝�Ƃ��Ēm���Ă��܂��B
| �藝 �ʑ���Ԃ��Z��������K��ԂȂ�A����͂��鋗����ԂƓ����ƂȂ�B�m�E���]�[���n |
�ȉ��C���̒藝�̓��e�𗝉����邽�߂̕K�v���������ɐ������Ă����܂��傤�B
�m�Q�n�@��������
�܂��A���K����̐����ł��B�ӂ����������ƌĂ�Ă���S�̏���������
| �iT1�j | �@��x�C��y �ix��y�j�@�ˁ@y ���܂܂Ȃ��ߖT N�ix�j�����݁B �@�@�@�@�@�@�@�@�@�@�@( x �� y ���������Ă����藧�� �� ) |
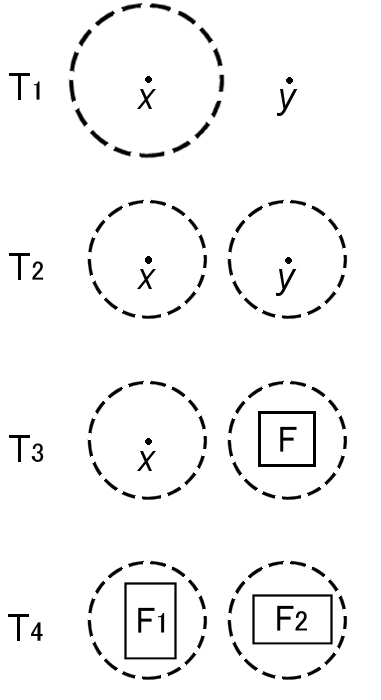 |
| �iT2�j | �@��x�C��y �ix��y�j�@�ˁ@�iT1�j�ł����āC �@�@�@�@�@�@�@�@�@�@�@�@�@�@����� N�ix�j��N�iy�j���ӂ����݁B |
|
| �iT3�j | �����̂Ȃ���x�A�W�� ��F�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�ˁ@N�ix�j��N�iF�j���� �����݁B |
|
| �iT4�j | �����̂Ȃ��W�� ��F1�A��F2�@ �@�@�@�@�@�@�@�@�@�@�@�@�@ �ˁ@N�iF1�j��N�iF2�j���� �����݁B |
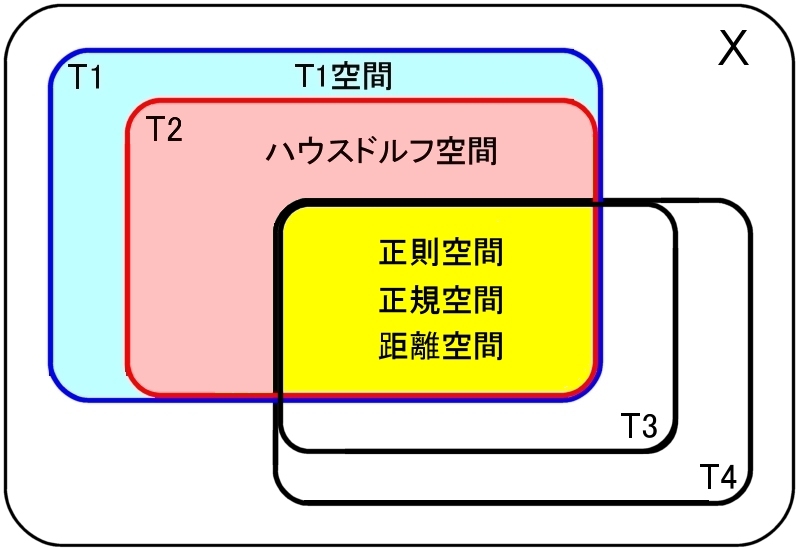
���������Ɋ�Â������I�Ȉʑ���Ԃ̖��́i���ށj�ɂ͈ȉ��̂��̂�����܂��B
�t���V�G��ԁF T1���݂����B �n�E�X�h���t����F T2���݂����B�@ �@�@�i�����I��T1���݂����B�j ��������F T3��T1���݂����B�i�����I��T2���݂����B�j ���K����F T4��T1���݂����B�i�����I��T2�CT3���݂����B�j
���̏��ɏ������������Ȃ�C�������������Ȃ��Ă����悤�Ɍ����܂��B����قǒP���ł͂���܂���B
�����̌��������Œ�܂�ʑ���Ԃ̕�܊W�������Ǝ��̂Ƃ���ł��B
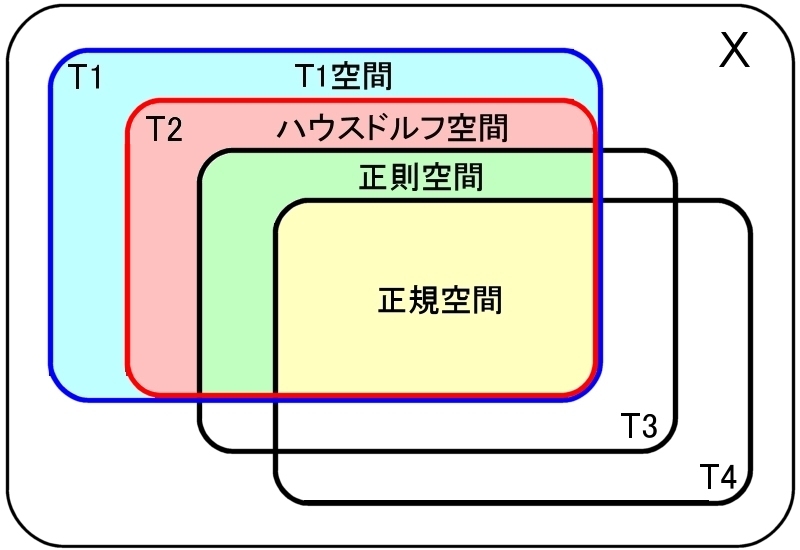
�m�R�n�@�e��Ԃ̊ȒP�Ȑ����ł��B
T1���
T1���������ʑ���Ԃł���C
| ����@�@�@ �ʑ���� X �� T1��Ԃł���C �i�P�j�@x��X �̓_�W���ox�p �͂��ׂĕW���ł���B(�t�����藧��) �i�Q�j�@X �̗L�������W���͂��ׂĕW���ł���B |
�Ƃ������Ƃ������܂��B
��P�@�@X��{a�Cb�Cc} �ŁC���U�ʑ�O 1����(X) �����ʑ����(X�C��(X))�̏ꍇ�ɂ��āC
O 1�F�o�ӁC{a}�C{b}�C{c}�C{b,c}�C{c,a}�C{a,b}�C{a,b,c}�p�@
F 1�F�o{a,b,c}�C{b,c}�C{c,a}�C{a,b}�C{a}�C{b}�C{c}�C�Ӂp
���C�i�P�j�C�i�Q�j���������Ă��邱�Ƃ��m�F�ł��܂��B�@�@
(��ʂɗ��U�ʑ���Ԃ�T1��Ԃł���C�L���W���ł͋t�����藧�B)
�m�S�n�@�@
T2��ԁ@�i�n�E�X�h���t��ԁj
T2��Ԃ��n�E�X�h���t����Ƃ������C�����ւ�d�v�ȋ�Ԃł��B
|
���� |
T2�����C�����I��T1���������Ă��܂��B
|
���� ���U�ʑ������ʑ���� (X�C��(X)) �̓n�E�X�h���t��Ԃł���B |
��Q�@�@X��{ a�Cb�Cc } �̈ʑ���� (X�C��(X)) �ɂ��āC
a��b�ɂ��āC
a���܂܂Ȃ�b�̋ߖT{b}�����݂��Cb���܂܂Ȃ�a�̋ߖT{a}�����݂��C{a}��{b}���ӁB
a��c�ɂ��āC
a���܂܂Ȃ�c�̋ߖT{c}�����݂��Cc���܂܂Ȃ�a�̋ߖT{a}�����݂��C{a}��{c}���ӁB
b��c�ɂ��āC
b���܂܂Ȃ�c�̋ߖT{c}�����݂��Cc���܂܂Ȃ�b�̋ߖT{b}�����݂��C{b}��{c}���ӁB
��T2�������m�F���邱�Ƃ��ł��܂��B
����ɁC���U�ʑ������ʑ���� (X�C��(X)) �́Cx�Cy��X �ɑ��Ď��̗��U���� d0 [#] �����o�����Ƃ��ł��܂��B
d0(x,y)�� 1�@�@�@(x��y) 0�@�@�@�ix��y)
���������āC�ʑ���� (X�C��(X)) �͋��������邱�Ƃ��\���ƕ�����܂��B����́C
| ���� ���U�ʑ������ʑ���Ԃ������t�\����ł���B |
�̋�̗�ł��B
��R�@�@�W�����CX���oa,b,c�p�C�ʑ����@O 4���o�ӁC{b}�C{a,b}�C{b,c}�C{a,b,c}�p
�Ƃ���ƁC(X�CO 4)�@�͈ʑ���ԂƂȂ�B�������C�n�E�X�h���t��Ԃł͂Ȃ����Ƃ͂����Ɋm���߂��܂��B
O 4�̓_�@a �� b �� c �ƌ݂��Ɍ����Ȃ��ߖT���������Ȃ��̂ŁC(X�CO 4)���n�E�X�h���t��Ԃł͂���܂���B
���������āC(X�CO 4) �͋�����Ԃł͂Ȃ����Ƃ�������܂��B
����
���U������Ԃ̈ʑ��͗��U�ʑ��łȂ���Ȃ�Ȃ����Ƃ�������̂ŁCO 4�̈ʑ������ʑ���Ԃ͗��U���������邱�Ƃŋ�����Ԃɂ͂ł��܂���B���U������� (X�Cd0) �̕����W�������ׂĊJ�W���ł��邱�Ƃ͈ȉ��̂Ƃ��莦���܂��B
O �� X �̔C�ӂ̕����W���Ƃ��܂��B�C�ӂ� x��O �ɂ��āCV��=1(x)��{ x }�@�Ȃ̂ŁCV��=1(x)��O ��������܂��B�Ȃ��Ȃ�CV��=1(x) ��x�̃�-�ߖT�ŁCx �Ƃ̋�����1��菬�������C���Ȃ킿x ���g�݂̂Ƃ������Ƃł����瓖�R O �ɑ����錳�ł��B����āCX�̕����W���͊J�W���ł��B�J�W���̒�` �� [#]
��S�@�@�]���Q���t���C���� (R�COs) �̓n�E�X�h���t��Ԃł���B�@
�ؖ�
R��̂Q�_p�Cq�@(p��q�j�̊�{�ߖT (p�|1/n�Cp]�C(q�|1/m�Cq] ���l����ƁC�����͊J�W���ŁC�\���傫��m���l����ƁCp��(q�|1/m) �Ƃł���̂ŁC
(p�|1/n�Cp] �� (q�|1/m�Cq] ���ӂƂł���B
|
���� �n�E�X�h���t��Ԃ̔C�ӂ̓_��́C��_�Ɏ�������B |
�w���@�ŏؖ��ł��܂��B
�n�E�X�h���t��Ԃ̓_�� {xk}�@���_ p �y�ѓ_ q (��p) �̂Q�_ (�ȏ�) �Ɏ�������Ȃ�C p ���C�ӂ��ߖT N(p) �Cq ���C�ӂ��ߖT N(q) �̗����ɑ��Ă��鎩�R�� n �����݂��āCk��n �ł��邷�ׂĂ� k �ɑ��āCxk��N(p) ���Cxk��N(q) �ƂȂ��Ă���B
����́C�n�E�X�h���t��Ԃɂ́CN�ip�j��N�iq�j���ӂ��� N(p)�CN(p) �����݂��邱�Ƃɖ�������B
�܂�C�n�E�X�h���t��Ԃ�ݒ肷��ƁC�P�_�Ɏ�������_��̋Ɍ����l���邱�Ƃ��ł����i���������l���邱�Ƃ��ł���C�K����������������K�v�͂Ȃ��j�̂ł��B
�m�T�n
T3��T1��ԁ@�i������ԁj
������Ԃ́CT2�������I�ɖ������Ă��܂��B�܂�C
������Ԃ̓n�E�X�h���t��Ԃł���B
�܂��CT3�������CT1�CT2�����Ȃ����Ƃ�����܂��B�ˁ@[#]
��P�@�@�]���Q���t���C���� (R�COs) �͐�����Ԃł���B
�ؖ�
���}���Q�l�ɂ���C(R�COs) �̔C�ӂ̕W�� A �Ƃ���ɑ����Ȃ� x �ɑ��āC�\�������ȃÂ�I�ׂC
x��U �ł���J�W�� U �����݂��āC���CU �̕�̕�W���ł���J�W�� [ U ]c �� A ���l����CU ��[ U ]c ���ӂƂ��邱�Ƃ��ł���B
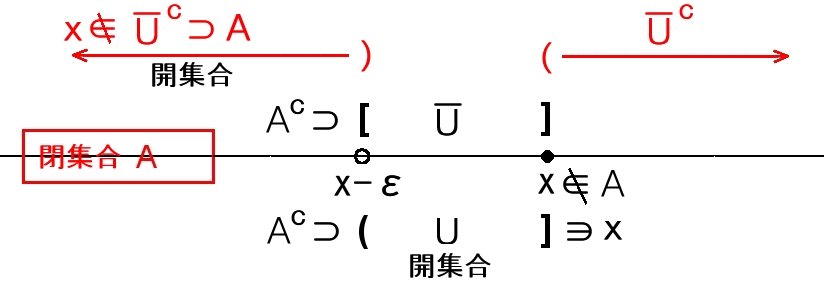
��S�@�@�ʑ����(X�CO 5) �͐�����Ԃł���B
O 5�F�o�ӁC{a}�C{b,c}�C{a,b,c}�p�@�@
F 5�F�o{a,b,c}�C{b,c}�C{a}�C�Ӂp
�Ȃ��Ȃ�C�����̖���X �̔C�ӂ̓_�ƕW���ɑ��Ď��̊J�W�������݂��܂��B
a��{b,c}�@�ɑ��āC�@{a}��{b,c}����
b��{a}�@�@�ɑ��āC�@{b,c��{a}����
c��{a}�@�@�ɑ��āC�@{b,c��{a}����
�����݂��܂��B
�Ȃ��CT3�����āCT1�����Ȃ��ʑ���Ԃ����݂��܂��B�ˁ@[#]
��T�@�@���U�ʑ���Ԃ͐�����Ԃł���B
�m�U�n
T4&T1��ԁ@�@�i���K��ԁj
���K��Ԃ͎����I��T2���݂����Ă��܂��B
���K��Ԃ̓n�E�X�h���t��Ԃł���B
�܂��C
���K��Ԃ͐�����Ԃł���B
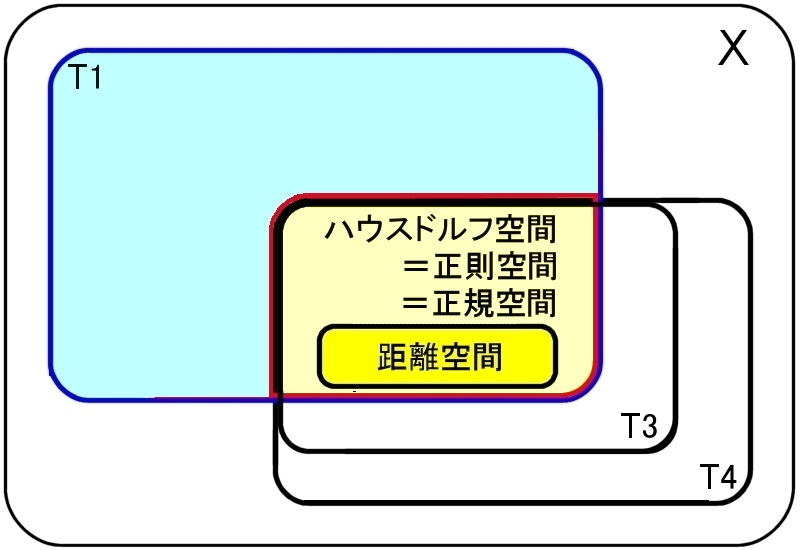
�ʑ���ԂƋ�����Ԃ̊�{�I�ȊW�Ƃ��āC
| ����@�@�@������ԁ@�ˁ@���K��ԁ@T1��T4�@�ł���@�@�i�ؖ��͒����j |
���������܂��B
�u�ˁv���u�́v�ƂȂ�̂́C�ʑ���Ԃ���Q�Z���� [#] �����Ƃ��ł���ƕ������Ă��܂��B
��Q�Z�����@�@�ˁ@������ԁ����K��ԁ�������ԁ��n�E�X�h���t���
��U �@ �]���Q���t���C�����@(R�COs) �͐��K��Ԃł���B
�ؖ��͐�����Ԃł��邱�Ƃ��������Ƃ��ƁC���l�Ȃ̂Ŏ����Ńg���C���܂��傤�B
�Ȃ��CT4�����āCT1�����Ȃ��ʑ���Ԃ����݂��܂��B�ˁ@[#]
�����܂ł̐�����}������Ǝ��̂悤�ɂȂ�܂��B
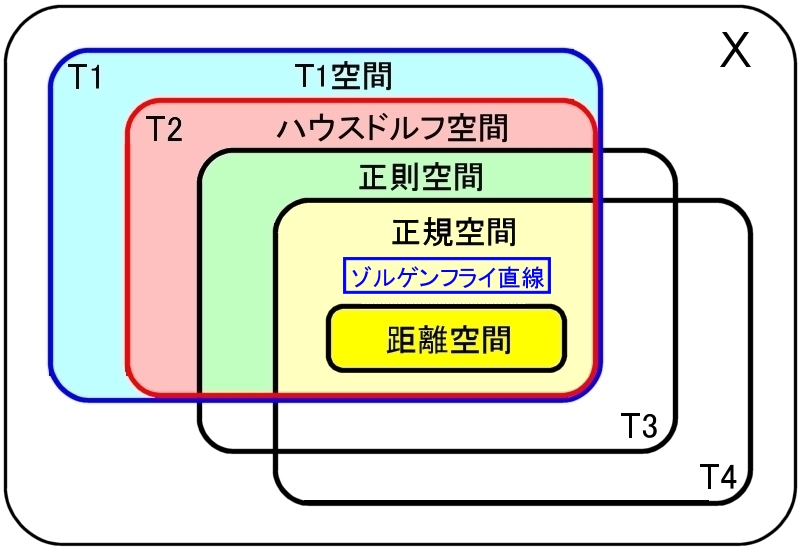 |
�� |  |
| ������ԂƐ��K��Ԃ̊W | ��Q�Z�����̒lj��� |
�������\�藝�̂Ƃ���ł�����x�������܂�
�m�V�n�@�������
�e�ʑ���� X �̕�����Ԃւ��i��`�I�ȁj�����́C
�i�P�j�@X �� T�P��ԂȂ�AX �̕������ A �� T�P��Ԃł���B
�i�Q�j�@X �� T�Q��ԂȂ�AX �̕������ A �� T�Q��Ԃł���B
�i�R�j�@X ��������ԂȂ�AX �̕������ A ��������Ԃł���B
�̂Ƃ�������p����܂��B�Ƃ��낪�C
�i�S�j�@T4 ��Ԃ̕�����Ԃ͕K������T4 �łȂ�
�܂�C�����ōl���Ă���S�^�C�v�̈ʑ���Ԃ̒��ŁC�����̃C���[�W�ɋ߂���Ԃɋ߂Â��邽�߂ɕK�v�ȏ����Ƃ��l�����鐳�K��ԂɂȂ�ƁC���̕�����Ԃ͌��X�̐��K��Ԃ̐����������Ȃ��Ƃ������Ԃ������Ă��܂��B�܂�C�����������߂�Ƌ�Ԃ��i�������`�I�ȁj�����������Ȃ��Ă��܂��B
* �n�E�X�h���t��Ԃ̏���� [#] ���n�E�X�h���t��ԂɂȂ�Ƃ͌���Ȃ��B
�m�W�n�@���ϋ��
�Q��T1��Ԃ̒��ϋ�Ԃ�t1��Ԃł���B
�Q�̃n�E�X�h���t���(�܂��͐������) �̒��ς́C
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�n�E�X�h���t���(�܂��͐������) �ƂȂ�B
����C2�̐��K��Ԃ̒��ς͕K�������Ăѐ��K��Ԃɂ͂Ȃ�܂���D
�i�����ʁ@R2 �̊J��� [a,b)�~[c,d) �ŕ\�����W���ł��B�j
�܂Ƃ�
��� ���̕������
�K������������̒��ϋ��
�K���������T1��� �Z �Z �n�E�X�h���t��� �Z �Z ������� �Z �Z ���K��� �~ �~
�~�@������Ԃ��W���Ȃ�Z
�m�X�n�@�R���p�N�g���
�R���p�N�g���n�E�X�h���t��ԁiT2��ԁj�̐����������Ă����ƁC
|
���� �R���p�N�g�ȃn�E�X�h���t��� X �̕�����Ԃ� S �Ƃ���ƁAS ���W���ł��邱�Ƃ�
S ���R���p�N�g�ł��邱�Ƃ͓��l�ł���B |
�n�E�X�h���t��Ԃ̃R���p�N�g�����W���͕W���ł��B
�p���R���p�N�g���n�E�X�h���t��ԁ@�@�ˁ@���K���
�Ǐ��R���p�N�g &�@�n�E�X�h���t��ԁ@�ˁ@�������
| ���� �R���p�N�g��� X ���� �n�E�X�h���t��� Y �ւ̘A���ʑ� f �ɂ���āC X �̕W�� F �̑� f�iF�j �͕W���ƂȂ�B |
����āC�R���p�N�g�łȂ��Ƃ��́CX�̕W�����A���ʑ��ɂ���āC�W���ł͂Ȃ��W���Ɏʂ���邱�Ƃ�����킯�ł��B��Ƃ��ẮC
X��[0�C��]�@�@�@�@�@�i�W���j
y��tan-1x�@�@�@�@�@�i�A�����j
Y��f(X)��[0�C1)�@�@�i�W���ł��J�W���ł��Ȃ��j
���グ�Ă����܂��傤�B
|
�藝 �R���p�N�g�ȃn�E�X�h���t��� X ����R���p�N�g�ȃn�E�X�h���t��� Y �ւ�1��1�A���ʑ�
f �����݂���Af-1���A���ł���B���Ȃ킿�AX ��Y �͓����ƂȂ�B |
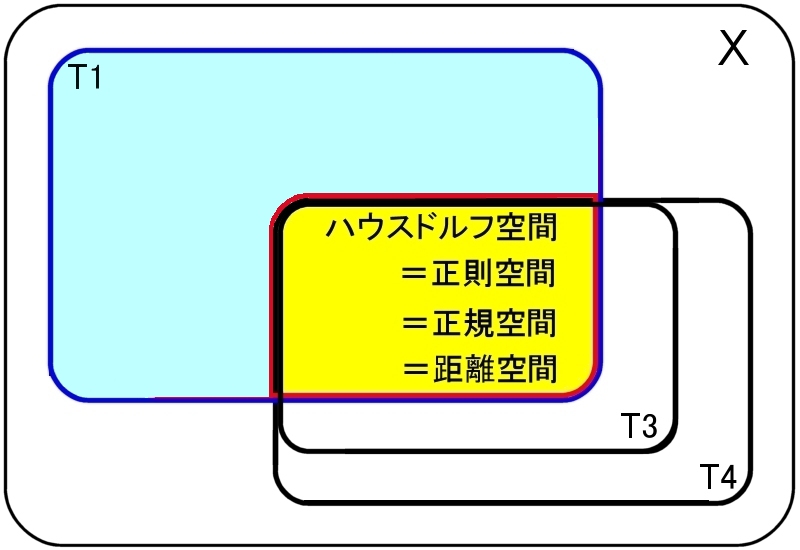
�m10�n�@�ʑ���Ԃ��R���p�N�g����ɐ��������ꍇ�́C
���K��ԁ�������ԁ��n�E�X�h���t���
����ɁC��Q�Z�������������ꍇ�́C
������ԁ����K��ԁ�������ԁ��n�E�X�h���t���
�}������ƁC
 |
 |
| �R���p�N�g��� | �R���p�N�g����Q�Z���� |
�m11�n�@�L���W���̏ꍇ
�L���W���̏ꍇ�C
�@�@
T1��ԁ@���@�n�E�X�h���t��ԁ@���������
�ƂȂ�܂��B
�����܂ŁC�L���W������Ȃ�ʑ���Ԃ̗�Ƃ��āC�p���Ă��� (X�CO k) �ƕ��������Ƃ̊W�����ꗗ�Ŏ����܂��B
���@�@�L���W�� X��{a,b,c} �Ɏ��̈ʑ�O k����ꂽ�ʑ���Ԃ̓���
|
|
F4�@��N�i{c}�j��N�i{b}) �́C{{a,c}�܂���{a,b,c}}��{{a,b}�܂���{a,b,c}}�����@�ˁ@F4��T4�����Ȃ��B
�m�S�n
���K����@�ɂ��Ă�����x�l���Ă݂܂��傤�B
�iT4�j�̈Ӗ��F�@�J�W��O �ƕW��F �ɂ��āA
F��O�@�@�ˁ@F��O�f��F�f��O�@�@�Ȃ�W��F�f�A�J�W��O�f�����݂���B
��������B����͌J��Ԃ����Ƃ��ł��āA�����
F��O�h��F�h��O�f��F�f��O�@�@�ˁ@F��O�h��F�h��O�f��F�f��F�f�h��O�f�h��O�@�@�ˁ@�ˁ@��
�Ƃ����悤�Ɂ@�i�W�����J�W���j�@��}�����čs�����Ƃ��ł��邱�Ƃ������Ă��܂��B
|
���� ���K���X �̋��ʕ������Ȃ���łȂ��W���� F0�CF1�C�܂��C���̊J�ߖT�� U(F0)�CU(F1) �Ƃ���Ƃ��C �@F0 ��U�iF0�j��U�iF1�jc��F1c�@�@ |
�Ȃ��Ȃ�C
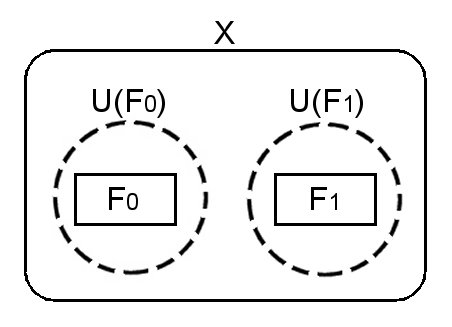
�ؖ��@�@��`���C
F0��U�iF0�j�@�@�́@U�iF0�jc��F0c �@�@�@
F1��U�iF1�j�@�@�́@U�iF1�jc��F1c�@�@�@�A
����ɁC
F0��F1���Ӂ@�@�@�@�@�@�́@F0��F1c�C�@�@�@�@�@F1��F0c�@�@�@�@�B
U�iF0�j��U�iF1�j���Ӂ@�́@U�iF0�j��U�iF1�jc�CU�iF1�j��U�iF0�jc�@�@�@�C
�̊W�������ɐ��藧���Ă��邱�Ƃ�������܂��B�������CF0��F1c�@�B�ł���Ƃ��C
�@F0 �@ �� U�iF0�j �� U�iF1�jc �� F1c �@�@�@�E�E�E�E�E�@[*] �W�� �@ �J�W�� �C �W�� �A �J�W��
���������Ă��܂��B����������ƁC�W��F0�Ƃ�����܂ފJ�W��F1c���^����ꂽ�Ƃ��C���̊ԂɁC�@�i�J�W�� U(F0) �� �W��U�iF1�jc �j�@���}���ł��邱�Ƃ������Ă��܂��B
�����ŁCU�iF0�j�̕�ɂ��āCU�iF0�j��[U�iF0�j]��U�iF1�jc �ł��邱�Ƃɂ����ӂ��āCU�iF0�j��U(1/2)�ƋL����������ƁC[*]�@������
F0 ��U�i1/2�j��[U�i1/2�j]��F1c�@�@�@�@���@�r���ɂ���@U�iF1�jc�@�͏ȗ�
�������܂��B����ɁC����1�Ԗڂ́��̉ӏ���3�Ԗڂ́��̉ӏ��ɓ��l�ɁC�i�J�W�����W���j��}�����邱�Ƃ��ł��C����� (U(1/4)��[U(1/4)])�C(U(3/4)��[U(3/4)]) �Ə������ƂƂ���C
F0��U(1/4)��[U(1/4)]��U�i1/2�j��[U�i1/2�j]��U(3/4)��[U(3/4)]��F1c�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@||
F0��U(1/22)��[U(1/22)]��U�i2/22�j��[U�i2/22�j]��U((22-1�j/22)��[U((22-1�j/22)]��F1c�@
�����n�K�J��Ԃ��ƁC��܊W�̂���W�����C
U(1/2n)�C[U(2/2n)]�C�E�E�E�E�CU�ik/2n�j�C�E�E�E�E�C[U�i(2n-1)/2n�j]
�������܂��B
�m�T�n
|
�E���]�[���̕�� ���K��� X �̋��ʕ������Ȃ���łȂ��W���� F0�CF1�Ƃ���ƁCX��̂���A���� f ��C(X) �����݂��āC f(X)���m0�C1�n |
��̓I�ɁC
Dn���om/2n�bm��0�C1�C2�C�E�E�E�C2n�p
D��Dn�@�@�@���Q�i�@�ŕ\����[0�C1]�̎����S�̂��Ӗ�����
�W�����F�oU(t)�bt��D�p�C�@�i0��t��1�j
�Ƃ��āCf�@�́C
| f(x)�� | �@�@�@�@�@1�@�@�@�@�@�@�@�@�@�@�@�@ | �i�ǂ�� t �ɑ��Ă� x |
|
| inf�ot��D�bx��U(t) �p | �i ���� t �ɑ��āC�@ x��U(t)�j |
�ŗ^������B
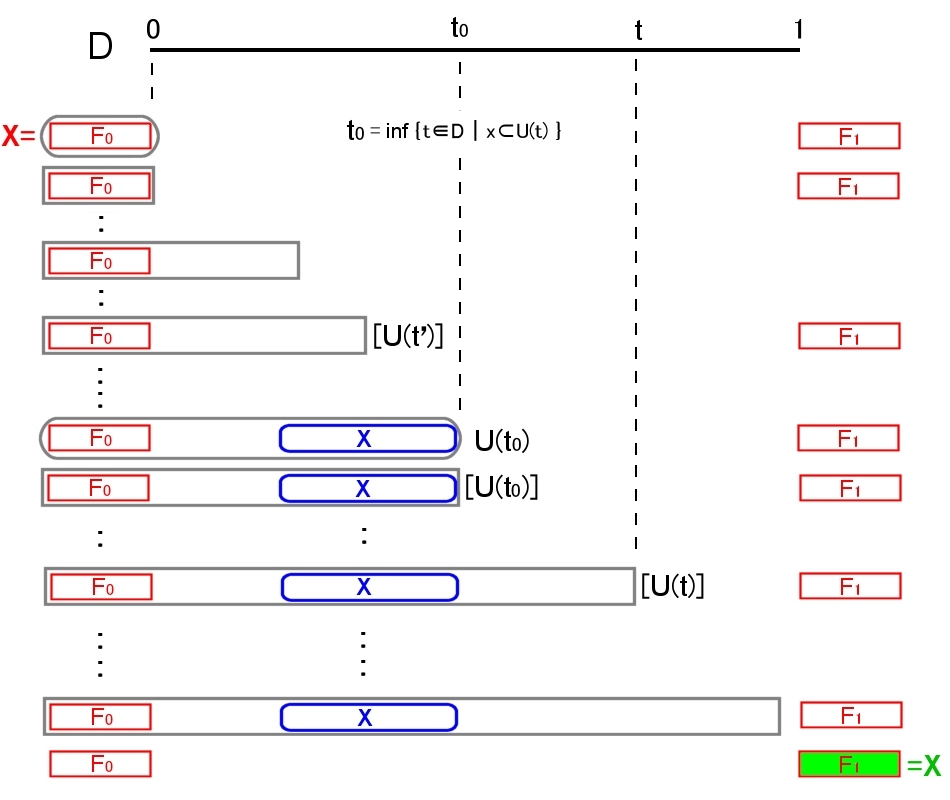
f(F0)=0�Cf(F1)��1�@�͎����B���̒��Ԃ�X�ɑ��Ă͏�}���Q�ƁB
f ���A�����ł��邱�Ƃ́C�J�W�� O���m0�C1�n�ŁCf-1(O) ���J�W���ł��邱�Ƃ��ؖ�����悢�B�i��}�j
�ʑ���Ԃ�������ԂƂȂ�������������߂ɗp������Ă����ƁC
|
��`�@�@�������\��� �i�P�j �ʑ����(X�CO )�ɑ��āCO ��O (d) �ƂȂ�悤�ȋ����� d �����݂���Ƃ��C�ʑ���� (X�CO ) ���������\�i��ԁj�Ƃ����B �i�Q�j�������\����Ƃ́A�u������ԁiY�Cd�j�ƈʑ����^�Ȉʑ���ԁiX�CO �j�v�̂��Ƃ������B ���Ȃ킿�C�ʑ����^�ʑ��Ղ��Cx�Cy��X�C����сC��(x)�C��(y)��Y �Ƃ���C���鋗���C d~�ix�Cy�j��d�i��(x)�C��(y)�j �����݂��āA���ꂩ�瓱�����ʑ���O �ł���悤�ɂ��邱�Ƃ��\�Ƃ������ƁB |
�������藝�F�ʑ���Ԃ��������\�ł��邽�߂̏\��������^����藝�Ŏ��̂悤�Ȃ��̂�����܂��B
| �E���]�[���́i�������\�j�藝 �i�P�j���Z�I����������͋������\�ł���B�i1926 �N�C�`�R�m�t�j �i�Q�j���Z�I�����K����͋������\�ł���B�i1925 �N�C�E���]�[���j �i�Q�j�f���Ȃ��Ƃ�2�_���܂ޘA���Ȉʑ���Ԃ��A���K��ԂȂ���̔Z�x�͎����̔Z�x�ȏ�ł���B |
�������\��Ԃ́C������Ԃ̂��ׂĂ̈ʑ��I�����������Ă���A�n�E�X�h���t��Ԃł���C���K��Ԃł��B

�������A�������̂悤�Ȃ������̋����̐����͈����p���܂���B
������C�u���ׂĂ̑��Z�I�ȑ��l�̂́A�������\�v�Ƃ����܂��B�܂����̒藝�̋t�͕K�������������܂���B
| �藝�@�E���]�[���藝�̌n �@�ʑ���� X ���Z��������K��ԂȂ�A����͂��鋗����Ԃƈʑ����^�ƂȂ�B |
��@�@�]���Q���t���C�����͋������\�ł͂Ȃ��B
�������\�ȃ��[�N���b�h��ԂƂ̔�r�ł��B
| - | �]���Q���t���C ���� |
���[�N���b�h�@ ���� |
| �ʑ� | Os�@�@�@ ���@�@�@OR | |
| �� �F Q��R���f�� | �� | �� |
| �R���p�N�g | �~ | �~ |
| �A���� | ���S��A�� | �ʏ�A�� |
| ��P�Z���� | �� | �� |
| ��Q�Z���� | �~ | �� |
| T1 | �Z | �Z |
| �n�E�X�h���t | �� | �� |
| ���� | �� | �� |
| ���K | �� | �� |
| �������\ | �~ | �� |
���S��A����Ԃ�T1 ����ł���B�@�@
�J���g�[���W���Ɋւ��āC
| �藝 �J���g���W���͗L�E�W���ł���B |
��������������e�̒藝�ł��B
|
�藝 �i�P�j�@�n�E�X�h���t�ʑ���Ԃ��R���p�N�g�������\�ƂȂ邽�߂̕K�v�\�������́A���ꂪ�J���g�[����Ԃ̘A�����ƂȂ邱�Ƃł���B f�FK��X �����݂���B�܂�C�C�ӂ̃R���p�N�g������Ԃ̓J���g�[���W�������邱�Ƃ��ł���B |
���S��A����Ԃ̘A�����͊��S��A���ł���Ƃ͌���Ȃ��B
���@�@��E�E