ときわ台学

	Appendix 2　集合族と濃度の計算
f-denshi.com [目次へ]　最終更新日：　04/11/15　(仮)
サイト検索

１．集合族

［１］　　解析学入門において，べき級数を議論するときに関数列なる概念を導入しました。そこでは関数をあたかもカズのように取り扱い，さらに，数の収束に対応させて関数列がある関数に収束する様態の一つとして一様収束なる概念を導入しました[#]。こういった取り扱いを集合論の立場からみれば集合の集合を考えていることになります。

　もうひとつ例をあげれば，閉区間［0,1］で定義される連続関数 y＝f(x) というときには，この連続関数 f(x) のひとつ一つを ”平面の部分集合＝曲線 ” と見ることもできます。したがって，閉区間［0,1］で定義される連続関数全体の集合と言うときは，「部分集合」の集合を考えていることになるのです。

［２］　そこで，このような集合を取り扱うために，きちんとした用語を定義しておきます。集合 X の部分集合の集合 β を部分集合族，または単に集合族といいます。(厳密には→[#])　集合族は添数(λ，n など ) を用いて，

β＝｛ A_λ|λ∈Λ ｝　　　　≡ ｛ A_λ ｝_λ∈Λ　
β＝｛ A_n |n ＝ 1，2，3･･･｝　　

などのように表します。ここで，添え数は必ずしも離散的である必要はありません。例えば，平面全体の部分集合である，

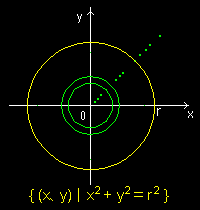
「半径： r∈R₀₊　をもつ円の集合」

は，R₀₊ を添数とする集合族であって，

｛ C_r ｝_r∈R₀₊　

ただし，C_r＝｛(x,y) | x²＋y²＝r²， r∈ R₀₊　｝

などと表すことができます。

［３］　とくに，添数としての半径を自然数に制限すれば，

｛ C_n ｝_n∈N＝｛C₁，C₂，C₃，･･･｝　

ただし，C_ｎ＝｛(x,y)|x²＋y²＝n²，　n∈N　｝

という，自然数を半径にもつ円全体の集合となります。このような可算個の元からなる集合族は可算集合族とか集合列といいます。

［４］　集合族の元(＝集合)に対して，ある数(ふつうは実数)を対応させる関数を集合関数と言います。

今の場合，円周上の点の集合をその半径に対応させる対応：

C_r　⇒　r　

は集合関数の例です。

［５］　最後に集合族の定義をきちんと書いておくと，　　( 上の例で，N → γ，C_n → γ として考えよ。 )

集合族の定義：
集合Γから集合 X のベキ集合 β(X) への写像：

f　：　γ　　→　X_γ　　　：　　γ∈Γ，　X_γ∈β(X)　　← f　は必ずしもβ(X)への全射ではない。

を定めることを，Γ を添数とする X の部分集合からなる集合族｛ X_γ ｝を定めるという。

２．集合族の濃度の演算

［１］　集合 A，B において，そのベキ，B^A を，B を A　の濃度だけ並べた直積集合，B×B×・・・・・×B　と定義します。　例えば，

A ＝｛ p，q，r ｝，B ＝｛ 0，1 ｝ならば，　⇒ B^A＝｛(b₁，b₂，b₃)| b₁，b₂，b₃ ∈B ｝

A

＝3，

＝2

B

というようになります。このB^A 集合の元 ( b₁，b₂，b₃ ) の総数は， 2³ ＝ 8個であることはすぐにわかりますね。

［２］　一方，集合 A から B への写像全体の集合を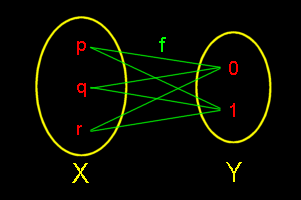

Map (A,B)

と書くことにします。今の例でいえば，p は f によって，0 か 1 に移る２通り，q，r についても同様に f によって，0 か 1 に移るかの２通りなので，この写像全体の集合は， 2³ ＝ 8個の元で構成されていることがわかります。

上のような元の計算の仕方から，

Map ( A，B )

＝

B^A

としていいことがわかります。

［３］　ここまで，集合 A，B が有限集合として説明してきましたが，この結果は無限集合についても適用できます。　特に A が可算基数をもつ集合 N のとき，

B^N＝B×B× ・・・＝

を考えることはそんなに難しくはないでしょう。　さらに，B ＝ R (実数の集合)であるならば，無限次元のユークリッド空間となります。( ここで，A が実数　R だと，ちと想像は難しいのですが，・・・)

なお，直積について

(１)　B^{(A₁凵A₂)}　～　(B^A₁)×(B^A₂)
(２)　(B^A₁)^A₂　～　B^(A₁×A₂)　

β(A)	⇔	Map( A，｛ 0，1｝ )
｛ φ ｝	⇔	( 0，0，0 )
｛ r ｝	⇔	( 0，0，1 )
｛ q ｝	⇔	( 0，1，0 )
｛ p ｝	⇔	( 1，0，0 )
｛ q，r ｝	⇔	( 0，1，1 )
｛ p，r ｝	⇔	( 1，0，1 )
｛ p，q ｝	⇔	( 1，1，0 )
｛ p，q，r ｝	⇔	( 1，1，1 )

は容易に確かめられます。

［４］　さて，A のベキ集合 β( A ) のそれぞれの元は，A の各元を含むか含まないかを指定することで識別可能です。これは，1 を ”含む”， 0 を ”含まない” とみなせば，集合 A からへ｛ 0,1 ｝への写像 Map ( A，｛ 0,1 ｝ ) と A のベキ集合 β( A ) の元とが，1 対 1 に対応しているからです。(右表参照)

結局，一般に，

β(A) ～　Map(A,｛0,1｝)

⇒

β(A)

＝

2^A

が成り立っています。

特に自然数のベキ集合の濃度については，

β(A)

＝ 2 ＝

/

となります。つまり，自然数のベキ集合の濃度は連続基数に等しいのです。この証明は，例えば連続基数濃度をもつ区間 (0，1］のすべての実数を(無限の)２進法で，　0．b₁b₂b₃　・・・・　と表せば，これを，

b₁ b₂ b₃ ･･･

↓ ↓ ↓ ↓↓

｛0，1｝ × ｛0，1｝ × ｛0，1｝ × ・・・＝ 2

/

のように１対１対応させることができることを利用して行なえます。つまり，自然数 N の集合のベキ集合 β(N) を考えると，その集合の濃度はNより大きくなるのです。これは一般化できて次の定理となります。

定理
任意の集合 A の濃度よりそのベキ集合β(A)の濃度は大きい，すなわち，

＜

β(A)

⇔

＜

2^A

［５］　濃度の演算について次のような関係をまとめておきます。

濃度の演算(計算)に必要な基本的な関係：
　　集合 X，Y の濃度を x，y　とすると，

(１)　X⊂Y　　⇒　x ≦y

(２)　2 ＝

/

(３)　2 ＝＞

- -

ベルシュタインの定理：　　
　　集合 X，Y の濃度を x，y　とすると，

(４)　x ≦y　かつ　x ≧y　　⇒　　x ＝y

証明：　いつか，そのうち，　・・・・・・

３．濃度の計算の例

* Xの濃度 Yの濃度直和集合 X凵Y 直積集合 X×Y ベキ乗 X^Y

(1)

X

Y

X

＋

Y

X

・

Y

X

Y

－

(2) x y
　x ＋y
　x y x^y 例

(3) y

(4) y

(5) x

(6) 自然数列

(7) 実数列

(8) x

-

(9)

-

(10)

-

不連続関数

ここで，(10) は一般に，R の濃度も R×R の濃度も同じ連続濃度であることをいっています。
また，x，y はある数を意味しています。

［目次へ］

補足　(あとでまた説明。)

(濃度の集合が整列集合を作っていることを認めれば，超限帰納法を用いて，)

_j ＋ _k ＝ _j ･ _k ＝ Max［ _j， _k ］

が成り立ちます。