| Appendix 4 完備 | ||
| f-denshi.com [目次へ] 最終更新日:04/11/9 | ||
| サイト検索 | ||
[1] 実数の連続性を実数の完備性とも言いました。[#] 実数解析入門で述べたように実数の完備性はユークリド空間 Rn 上に解析学を構築する上でも最も重要な公理であり,「極限値」なるもの(=解析学) の存在を正当化するものです。この状況は一般的な ”距離空間上の解析学” においても全く同様です。 距離空間における完備性の厳密な定義を述べると,
定義1:
距離空間 X において任意のコーシー列が必ず X の点に収束するとき,「X は完備である。」 |
となります。ここで,コーシー列とは,m,n→∞ のとき,|am−an|→0 となる点列 {an}; (an∈X)です。[#]
実数 R (1次元ユークリド空間(R,d))の連続性を,
| 「任意のコーシー列 {rn}に対して, | rn=r が R に存在する。」 [#] |
と述べることは,ここでの完備性の定義に沿った言い方なのです。 実数の場合,点列=数列です。
[2] もう一つ,定義を与えます。
|
定義2: (1) 完備な距離空間 (X,d) の部分集合 S について,その閉包が X に等しい,すなわち,
であるとき,S は(X,d) で稠密という。 (2) 距離空間 (X,d) の可算濃度をもつ部分集合 E の閉包 [E] が X に等しいとき,X を可分な集合という。 |
上の定義において,
S,E ⇒ 有理数
X ⇒ 実数
とすれば,上の定義は有理数,実数の関係をもったいぶって言い表したにすぎないことがわかります。すなわち,
(1) 有理数 Q の閉包 [#] は実数 R なので Q は稠密。
(2) 実数 R の可算濃度をもつ部分集合 Q の閉包は R なので実数は可分な集合です。
この用語は,ある距離空間がユークリッド空間にどこまで似ているのか,ユークリド空間上と同じような微分・積分学が構築できるのかどうかを判定するために使われる概念のひとつです。特にこの性質をもっているかどうかでその空間(ヒルベルト空間)に正規直交基底が存在するかどうかが決まります。⇒ リース・フィッシャーの定理の証明 [#] ⇒ ヒルベルト空間の弱収束 [#]
位相空間(必ずしも距離が定義されている必要はない)では,位相空間Xの部分集合Sが「Xで稠密である」とは,Xの任意の開集合O(≠φ)が,S∩O≠φを満たす [#] ことを言います。
[3] さて,具体的に関数の集合を元(=ユークリッド空間の点に相当)とする距離空間を見ていきましょう。関数を元とする距離空間において,コーシー列とは,
m,n → ∞ のとき,d(fm−fn) → 0 となる関数列 {fn}; (fn∈X)
ということになります。ただし,関数どおしの距離はいかようにも定義可能で,前ページの例をもう一度書くと,
| [A] X=閉区間[a,b]上の連続関数,C[a,b] (C[a,b],d(f,g)) |
d(f,g)=Max|f(x)−g(x)| ; a≦x≦b | ||||
| [B] X=閉区間[a,b]上の連続関数,C[a,b] (C[a,b],d1(f,g)) |
|
などがあります。どちらの距離を採用しても,コーシー列 fn は n → ∞ のとき,ある f にどこまでも近づいてゆくのですが,その様子はかなり違っています。
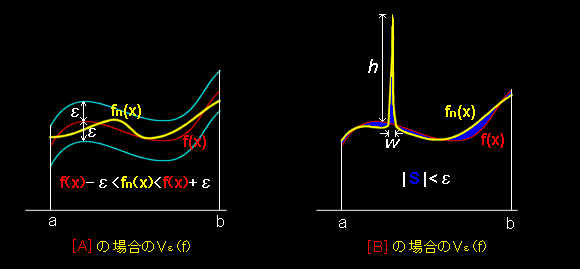
[A]では,実解析入門で述べたいわゆる ”一様収束”[#]と同様に fn は,n が十分大きければ,εを任意正数として, f ±ε の帯の中に fn はすっぽりと収まらなければなりません。
ところが,[B]の距離を採用した場合は,どんなに大きな n を考えても (どんなに fn が f に近づいたとしても),fn は f ±ε の帯の中に収まる必要はありません。例えば,ある点 x0∈[ a,b ] で|fn(x0)−f(x0)|= h >>1 を満たすような関数 fn を選んでも,f(x)から大きくはずれる範囲 W を十分小さくすれば,距離 d1 (図中の青で示した面積 S)をいくらでもいくらでも 0 に近づけることが可能だからです。
したがって,ε-近傍 Vε(f) [#]を考えるならば,[A]と[B]とでは性質の異なる関数 fn をそこに含んでおり,
「距離空間 [A]と[B]とでは近さの概念が異なる。」
ということができます。このように距離,すなわち,関数の集合への位相の与え方によって[#],関数どおしの ”近さ” は全く違ったものになります。 そして,この近さの概念の違いは距離空間としての完備性に影響します。
すなわち, 距離空間[A]において,f は必ず連続関数となり,完備であろうと考えられます。一方,[B]では,fn は実数解析入門で挙げた一様収束でない例 [#] のように不連続関数に近づくことがあり,極端な場合,いたるところで不連続なディリクレ関数のような不連続関数にも近づくことも可能です。つまり,その距離空間は完備ではないということになります。
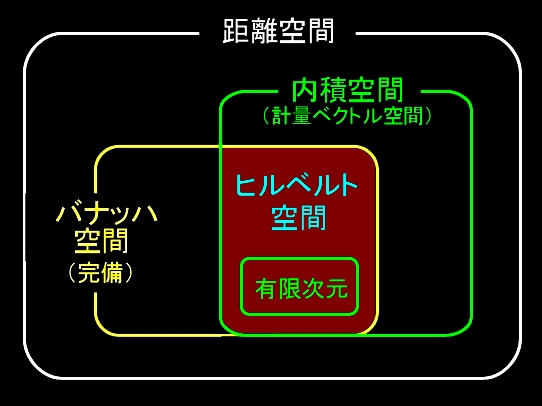
完備な距離空間をバナッハ空間という。
内積が入ったバナッハ空間がヒルベルト空間である。
本文中[A]はバナッハ空間であるが,[B]はバナッハ空間ではない。
例:関数の集合における完備化
閉区間[0、1]で定義される連続関数全体の集合:C~[0、1]
C~[0、1] ⇒完備化⇒ L1[0、1] (1位のルベーグ空間)
測度空間は完備とは限らないが,完備化することができる。
何を以て収束とするかによって完備性は違ってくる。
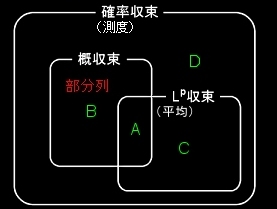
| 測度収束: | μ(x∈R:|fn(x)−f(x)|>ε)=0 |
| 概収束: μ{ | x∈R| | fn(x)≠f(x)}=0 |
| Lp収束: | ||fn−f||p=0 |
f=f(x)=0