| 5−2 一様収束 | ||
| f-denshi.com [目次] 最終更新日:08/02/11 | ||
| サイト検索 | ||
べき級数関数のいくつかの重要な定理とテイラー級数展開との関係について説明します。
[1] 次の定理はベキ級数関数の最も重要な性質です。
| 定理1 ベキ級数関数は収束域において連続である。 |
[2] この定理は次のより一般性のある定理の具体例のひとつとなっています。
| 定理2 閉区間 [a,b] で定義された連続関数 fn(x)の列 が,n→∞ のとき,f(x)に一様収束するならば,[a,b] で f(x) は連続関数である。 |
ここで,
fn(x) がf(x) に一様収束するとは,
(1) n → ∞ のとき,x が [a,b] を動いたときの|fn(x)−f(x)|の上限が 0 にいくこと,すなわち,または,ε-δ 論法を使うならば,
sup |fn(x)−f(x)|=0 x∈[a,b]
(2) どんな正数ε をとっても x によらないある番号 N が存在して,
n>N ⇒ | fn(x) − f(x) |<ε が 区間 [a,b] で成り立つ。
[3] この定理1の主張を定理2を適用できるように言い直すと,
| fn(x) | n | rkxk= r0 + r1x + r2x2 + ・・・ + rnxn | |
| Σ | |||
| k=0 | |||
「 定理1': 連続関数の列,f0(x) = r0
f1(x) = r0 + r1x
f2(x) = r0 + r1x + r2x2
fn(x)= n rkxk = r0 + r1x + r2x2 + ・・・ + rnxn Σ k=0
・・・・・・・・・・・・・・・・・・・・・・
が n→∞ で行きつくところの関数 f(x) は連続関数である。」(←もちろん収束したらの話ですが。)
となります。
はじめてこの定理を聞いた人は,''連続関数の列 {fn(x)} が n→∞ の極限において連続関数に収束するのは当たり前と思うかも知れません。
なぜ,「一様収束」のような条件が必要なのか直感的にはピンとこないのが普通でしょう。
ところが,ある集合の元から無限個の元をとり出して作った点列の収束先が必ずしもその集合の元に属さないことは,すでに1章でその実例を見ていたのです。つまり,半開区間
(0,1] の有理数全体の集合 A*から点列:
1 ,, 1 , 1 ,・・・, 1 ,・・・ 1 2 3 n
を選び出すと,n→∞ の極限における収束値は0ですが,0 は集合A*の元ではありません。この簡単な例から,連続関数の列の収束先が連続関数だと決めつけてかかるのは危険だと感じるワケです。
[4] 他にある集合の元の列の行き先がその集合に属さない典型的な例として,有理数の列の行き先が必ずしも有理数ではなく,無理数であることを挙げることができます。例えば,円周率πの少数第n位までとった有理数を第n項とするコーシー列{an},
a1=3.1, a2=3.14, a3=3.141,・・・・ :(|am−an|<10min{m,n})
を考えると,この列の収束する点は無理数 π であって有理数ではありません。初級レベルではこの定理はどうでもいいように思えますが,量子力学の体系がどこまで本当に信用なるのかというようなレベルになってくるとたいへん重要となってきます。さて,定理2の略証を以下示しますが,興味ない方は[6]に進んでください。
[定理2の証明の考え方]
[5] f(x) の連続性を,
|x1−x0|→ 0 のとき,εf =|f(x1)−f(x0)|→ 0 となる。
を示すことで証明します。
その際,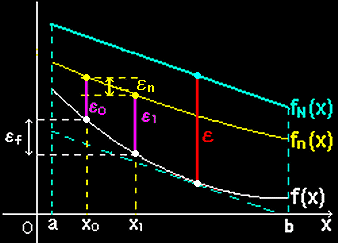 右図を使って話を進めます。 x1,x0,f(x0),f(x1),fn(x0),fn(x1) の相対的な位置関係は f(x) によって多様ですが,一般化してもメリットは少ないのでこれで説明します。
右図を使って話を進めます。 x1,x0,f(x0),f(x1),fn(x0),fn(x1) の相対的な位置関係は f(x) によって多様ですが,一般化してもメリットは少ないのでこれで説明します。
まず,fn(x) が f(x) へ一様収束するとは,
「どんな(小さな)正数εをとっても x によらないある番号 N が存在して,
n>N ⇒ |fn(x)−f(x)|<ε
が区間 [a,b] において成立する。」
ということを確認しておきましょう。
(図に示すように fn(x)は区間[a,b]において,fN(x)と f(x) とで,上下はみ出すことなく完全に挟まれているということです。)
また,図を参照して,
ε: |fN(x)−f(x)|の区間 [a,b] での上限(〜最大値)
ε1:|fn(x1)−f (x1)|
ε0:|fn(x0)−f (x0)|
εn:|fn(x1)−fn(x0)|
という量を定義します。ここで,εf :
(1) εf : | f (x1)−f (x0)|= εn+ε1−ε0
を評価したいのですが,関数 fn(x)の連続性より,
(2) |x1−x0|→ 0 ⇒ εn → 0
さらに fn(x) がf(x) に一様収束することから任意のεについて ,n>N のとき,
ε1 <ε (x1にて収束するので)
ε0 <ε (x0にて収束するので)
つまり,
(3) |ε1−ε0 | <ε
が成り立ちます。 したがって,(1),(2),(3)より,n > N ならば,
|x1−x0|→ 0 ⇒ εf =| f (x1)−f (x0)|< ε
がわかります。つまり,f(x)が連続関数だということが証明されました。
| 一般的な証明も,(a) fn(x)の連続性よりεn→0,(b) f(x)への一様収束性よりε1,ε0→0 を利用することで証明できます。 |
[6] この証明において,「一様収束性」が威力的な理由は,ただ一つのεを用いて,定義域全体にわたる関数値の性質を制限できることです。もちろん,これはたいへん強い要請であり,より高級な解析学ではこの性質をはずそうと努力するのです。 ⇒ ルベーグ積分
[7] 先へ進む前に連続関数 fn(x) が,n→∞ のとき f(x) に収束しても一様収束でないときは,必ずしも f(x) が連続関数にならないという例を挙げておきましょう。
fn(x),(n=自然数)を [ 0,∞) で定義された関数を,
fn(x)= 0 x ≦ 1 n(x−1) 1 < x ≦ 1+1/n 1 1+1/n < x
とします。図に描くと下のようになります。
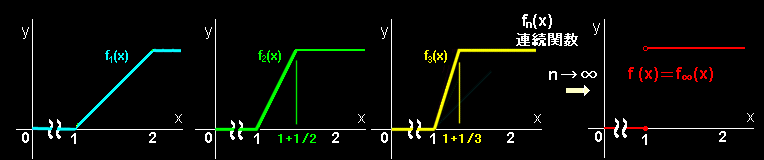
fn(x)は確定した任意の自然数nについて連続関数です。しかし,n → ∞ の極限を考えると,
f(x)= 0 (x ≦1) 1 (1<x)
という関数f(x)に収束しますが,この f(x) は x = 1 で連続ではありません(上図右端)。これはfn(x) がf(x) に収束してもそれは一様収束ではないから起こったことです。つまり,区間,1 < x ≦ 1+1/nでは,
Δf =|fn(x)−f(x)|=|n(x−1)−1|
なのでどんな n > N に対しても十分 x が1の近く(x−1 << 1/n)では,Δf
〜 1 とでき,Δf <ε(任意の正数) とすることができないからからです。
[1]「一様収束」のような高級な概念を大学初年度に教えることが多い理由は次の定理の説明に必要だからです。その定理とは,
| 定理3 ベキ級数関数 f(x) = r0 +r1x +r2x2 + ・・・ +rnxn + ・・・ は収束域(-r,r) で,C∞級の関数である。また,その導関数は,項別に微分して, f'(x) =r1 +2r2x + ・・・ +n・rnxn-1 + ・・・ となる。[項別微分可能] |
この定理から
ベキ級数関数 ⇒ テイラー展開可能な関数 |
ということになりますが,この逆もいえます。
[2] 要するに,テイラー展開の基本的な性質をきちんと証明するときに「一様収束」なる概念が必要なのです。大学レベルの数学(+他の科目も似たりよったりでしょう)になると,ものごとを,
「体系的に説明すること」 と 「やさしい順番に説明すること」
を一致させることが必ずしもできなくなる。それが教える側,教わる側双方にとってのストレスになっていると思う。改善の余地はまだまだあると思われるが,永遠に解決不可能な部分も少なからず含んでいる。
[3] 定理3の後半のに含まれている肝要な点は,極限の交換が可能となっていることです。どういうことかというと,べき級数関数について,
f'(x)= f(x+h)−f(x) h
= fk(x+h)− fk(x) 1 h
= fk(x+h)−fk(x) h
⇔ fk(x+h)−fk(x) h
= f'k(x)
という計算が可能であること,すなわち,途中⇔のところで,limh→0とlimn→∞の2つの極限の順序はfk(x)が一様収束であるならば,交換が許されるということです。
| これは, | と | が交換可能ということもできます。 | ||
[4] 同様な極限の交換として,項別積分可能性,
fk(x)dx = fk(x)dx
があります。これもfk(x)が積分区間で一様収束するならば,積分と無限和という極限の交換が許されることに基づいています。まだ,積分の話はしていないので,これ以上詳しいことはここでは省略。こちらを見てください ⇒ [#]
定理2の略証
n>N のとき,三角不等式から
εf =| f (x)−f (x0)|=|{f (x)−fN (x)}+{fN (x)−f (x0)}|
≦|f (x)−fN (x)|+|fN (x)−f (x0)|
≦|f (x)−fN (x)|+|fN (x)−fN (x0)|+|fN (x0)−f (x0)|
=ε+εN+ε0 この3つは共通にとれる。
ε: |fN(x)−f(x)| 一様収束
ε0:|fN(x0)−f (x0)| 一様収束
εN:|fN(x)−fN(x0)| 連続性