|
１ 実数 | |
| f-denshi.com [目次] 最終更新日：07/07/15 | ||
| サイト検索 | ||
［１］ 実数 x から実数 y への対応 f を実数上の関数 ( function )，または写像 ( map , mapping ) といい，
f ： x → y または， y ＝ ｆ(x) ← x の像は yであるというような言い方もします。
と書きます。x のとり得る範囲をこの関数の定義域 ，そのときの ｙ のとり得る範囲を値域 といいます。しばしば，関数を視覚的に表現するために x-y平面上にプロットしますが，その技法の説明はここでは不要でしょう。
定義域，値域の集合としては離散的な集合，例えば，整数などを考えることも可能ですが，解析学の舞台として使われるのは実数 ( real number ) と呼ばれる集合です。そこでこの用語の説明から解析学の講義を始めましょう。
［２］ 実数についての高校生レベルの説明は：
「実数とは大小を考えられるすべて数からなる集合で，無理数 ( irrational number) と有理数 ( rational number ) とから構成されている。有理数は分数で表せる数，無理数は分数では表せない数である。」
というところでしょう。ほとんどの人，とくに応用にだけ興味のある人にとってはこれでも十分なのですが，いくつか注意を付け加えることにしましょう。 大学の講義では「実数の存在」は公理として，つまり証明なしで受け入れるべき前提の一つとして，解析学の講義の最初の方に出てくるのが普通です。表現方法はいろいろありますが，高校のときより謙虚な仕方で提示され，しかも実数の連続性 ( continuity axiom ) というところがやたらと強調されています。
しかし，”連続＝連なって続いている”という言葉の響きから，実数の連続性の公理の意味を，「適当に一つの実数 a を選ぶと，その実数にいくらでも近い別の実数が必ず存在する」と捉えると，極めて不十分な理解になります。なぜなら，有理数(＝分数)の集合についてもある有理数についていくらでもそれに近い有理数を考えることができるからです。この有理数にもあてはまる性質は稠密性 ( dense ) と呼ばれ，実数の連続性とは区別されます。つまり，”ある数にいくらでも近い別の数が存在する” という性質を連続性といっているのではないのです。では，連続とは何なのでしょうか。実はこの問題は解析学の本質的な問題を含んでいるたいへん難しいものです。したがって，ここでは”連続”という言葉が使われる理由を直感的に理解することを目標としてガマンすることにします。
［３］ 実数，有理数の集合に共通する特徴である，「数を選び出して大小の比較ができる」ことに着目してみましょう。まず，有理数の集合を考えて，その中から一つ数を選び出します。するとその数を境界にして，より大きな有理数からなる集合とその数より小さな有理数からなる２つの集合が作られます。(選んだ数自身も一つの集合と見れば３つですが。)ところが，このような２つの有理数の集合の作り方は選び出される”ある数”が有理数でなくても可能です。例えば，有理数に属さない無理数：
2 (2の平方根＝1．4142･･･)
によってもこの数より大きな有理数の集合とこの数より小さな有理数の集合を作れます。すると，この
”事実” はいかにも有理数だけでは”隙間”があいているように見えるではありませんか！
この説明だけではよくわからないは人は，有理数よりずっと不連続に見える整数の集合を考えるともっとわかりやすいかもしれません。まず，整数の集合を考えて，整数に属さない有理数：
1.5
によって整数の集合を１以下の小さな整数の集合と2以上の大きな整数の集合に2分することを考えます。この様子は整数の集合がとびとびであるがゆえに，整数ではない数
1.5 によって整数の分断が起こったと感じられます。つまり，よそ者に割り込まれる余地があるとき，その集合は連続的ではなく，飛び飛びに存在して，隙間があるようにみえるのです。 ”連続” という言葉使いはこういうところからきているのだろうと推察できます。
［４］ では，どうしたら完璧に ”連続した数の集合” はつくれるのでしょうか。答えは，深く考えなければ簡単です。先の例でいえば，無理数 21/2 を有理数の集合に加えて新しい集合を考えれば，少なくとも 21/2 に起因する有理数の不連続性は解消されます。 ということならば，これを繰り返して有理数に割り込んでくるすべての数を有理数の集合に追加すれば，不連続点はなくなり，”連続的に並んだ数の集合”ができあがると考えられますね。そこで，その究極の
”順序関係の決まるすべての数からなる集合” の存在を認めよう，それを実数の集合と呼ぼう。
というのが 実数の連続性の公理 が意味するところなのです。ですから，実数のこの性質は，連続というよりすべての”順序のある数”を完全に尽くしている集合ということで”完備”とか”完全”という言い方(英語はcomplete, completion という)がふさわしいネーミングなのです。実際，高級な解析学ではそちらの用語の方が好んで使われます。
なお，上の説明では，無理数を具体的にどうやって一つ一つ探し出すんだ(実際，1つ，２つ，・・・と数えながら無理数を有理数に追加していったのではいつまでたっても実数の集合には到達しえないということがわかっています！)というようなプロセスの問題やこんな公理をつくって数学の理論体系に矛盾は生じないのだろうかといった問題（実数論の無矛盾性）を残してしまいますが，それは(集合論，数学基礎論などの)専門家になったら勉強してください。
実数の連続性については他にもいろいろな言い方があります → [#]
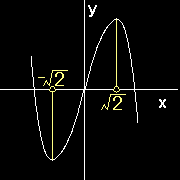［５］ 次に実数の集合を考えることがなぜ，解析学において大切なのか一つ例を示しておきましょう。ある集合上で定義された，関数，
f(x) ＝ -x3＋6x
を考えます。これを微分すると，
f ’(x) ＝ -3(x2−2)
となります。実数の集合で考えれば，この関数は，
x ＝ − 2 で極小値
x ＝ ＋ 2 で極大値
を取りますが，もし，有理数の範囲だけで考察すると，極大，極小値ともに存在しないという結論になってしまいます。グラフにすれば，有理数，実数どちらを定義域として考えても同じ図しか描けないということは注意に値します。たとえ，どんなに解像度をよくしても，有理数，実数ど
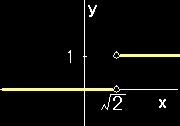
ちらを座標軸に用いたグラフの曲線の見た目には隙間を描くことは稠密性からできないのです。したがって，図示できることとある数が存在することとは直接関係がないのです。２の平方根，円周率πを図示できるからといって，それらが存在することの証明にはなりません。その存在は公理として解析学に持ち込まれているのです。他にも実数の存在を認めないと，直感的にはどうみても値が跳んでいて不連続としかいいようのない関数が連続関数の定義を満たしていることになってしまい，甚だ見苦しい理論体系になってしまいます。（そのような写像にばかりに興味を持つ人もいるには違いないが，･･･）
|
右図で示した関数は，x∈Q（有理数）で考えると連続関数に分類される！
|
 |
［６］ 上の例では，無理数 21/2 は代数方程式： x2−2＝0 の解となっていました(代数方程式の解とは何か厳密な定義は難しいのでここでは根号で表せる数くらいに考えてください)が，代数方程式の解とはならない超越数と呼ばれる無理数も存在します。これについてはオーソドックスながら有名な金利の話を紹介しておくのがいいでしょう。半年複利という金利計算方法がありますが，これは半年ごとに利息を元金に組み入れて利息を計算するというしくみです。どういうことかといいますと，金融商品の利息は１年当たりの利息で表示されています。たとえば，利息100％ということは，100万円預けると，1年後に100万円の利息がもらえるということです。年利計算では，1年たってはじめて利息が残高に反映され，1年後に預金残高が100万円から200万へ円と２倍になります。 これでは利子がつくまでの期間が長いので半年ごとに利息をつけようというのが半年複利です。
このとき，年率換算での支払い利息が100％と相違ないように半年の利息を設定するにはどうすればよいでしょうか。もちろん，1年分の利息の半分，50％が答えではありません。
1 ＋ x ＋ (１＋x)x ＝ (1＋x)2 ＝ 2 (倍) (元金) (半年後の利息) (１年後の利息) (１年後の残高)
を解いて，x ＝ 0.414213･･･，つまり，
41．42 ［％/半年］ (正解)
とすればよいことがわかります。
［７］ もし，間違って 1年の半分 50％ として計算すれば，
(1＋0.5)2 ＝ 2.25 (倍)
すなわち，年率 125％ となって銀行は払いすぎ，預金者は貰いすぎということです。
それでは，この間違った方法で，利子を半分にして年２回払う，利子を３分の１にして年３回払う・・・という計算を続けて，利息の元金への繰り入れを頻繁にすれば，利払い額はいくらでも膨らんでくのでしょうか。つまり，このように利払い頻度を無限大(∞)にしたとき，利息は無限大(∞)になるのでしょうか。 年３回利払いでは，
1 ＋(1/3) ＋ (１＋1/3)(1/3) ｛1＋(1/3)＋(１＋1/3)(1/3)｝(1/3) (元金) (1/3年後の利息) ((2/3)年後の利息) (１年後の利息)
＝｛1＋(1/3)｝3 (倍) (１年後の残高)
のように計算できるので，(1/n)年複利 では，１年後の残高は，
⇒ １年後の残高 ＝ ｛1＋(1/n)｝n ≡ xn (倍)
となります。ここで，x1，x2，･･･，xn，･･･ を無限数列とみなせば，
x1＜x2＜･･･＜xn＜･･･
が成り立っているので，確かに利息の支払い回数を増やすと１年後の残高はどんどん増えていくようです。
［８］ しかし，どんな大きなnであっても，
xn ＜3 (もちろん，2 ≦ xn )
であることも容易に示せます [ 問題 ］。 つまり，xn は n とともに限りなく増加してはいくのですが頭打ちになっているのです。このような状況では，n →∞ のとき，xn は２と３の間のある数に限りなく近づいてゆくと考えることは自然です。実際，その行き先の数とは高校生のときにすでに教わった，
e ＝2.71828182･･･ ［ネイピア数 ： 自然対数の底］
であり，いかなる方法でも最後のケタまできちんと数値を書き示すことが不可能な ”巡回しない無限小数” ＝無理数 です。
解析学における実数の連続性とは，その近づいてゆく，”行き先”を実在する数として ”認める” ということと同等なのです。
そして，大掛かりなので省略しますが，この数 e が代数方程式の解になりえない超越数 ( transcendental number ) であることも証明されています。他には円周率π＝3.142592････なども代数方程式の解とはならない超越数です。数の話の最後に特別な名前のついた実数の部分集合をまとめておきます。
実数 有理数 ･･-1，0，(1，2，･･･) 整数(自然数) 代数的数 1/2， 3/7，･･･ 真分数 無理数
2
e，π，
2
2 - ･･･ 超越数
［１］ 上の考察では，2＜xn＜3 であることが重要なポイントとなっていましたが，このような大小関係を押さえて議論を進めることは解析学全体を通してしばしば現れます。そこで実数の連続性に基づいた基本用語を一つ説明しておきましょう。とりあえず，次の定義を読んでみてください。
| 定義： 集合 M について， (１)実数R の部分集合 M が上に有界とは，ある数 k ∈R が存在してすべての x ∈M に対して， x ≦ k であること。また，そのような k 全体の集合を M の上界という。 (２)M の上界の最小値を M の上限 ( supremum ) といい，sup M と書く。 |
および，
| 定義： 集合 M について， (１) 下に有界と下界， 実数 R の部分集合 M が下に有界とは，ある数 k ∈R が存在してすべての x ∈M に対して， x ≧ k であること。また，そのような k 全体の集合を M の下界という。 (２) 下限 M の下界の最大値を M の下限 ( infimum ) といい，inf M と書く。 |
また，上にも下にも有界 ( bounded ) である場合は単に ” Mは有界である ” といいます。これらの定義はさっと読んだだけではふつう，ちんぷんかんぷんで何のことだかわかりません。そこで，連続した実数のある部分集合(区間という)について上の用語を適用してみましょう。
［２］ ２つの実数 a，b に挟まれた実数の部分集合に次のような名前をつけます。
記号 集合 区間の名 最小値 最大値 (１) ［a,b］ ｛x｜a≦x≦b｝ 閉区間 a b (２) (a,b) ｛x｜a＜x＜b｝ 開区間 なし なし (３) (a,b］ ｛x｜a＜x≦b｝ 半開区間 なし b (３)’ ［a,b) ｛x｜a≦x＜b｝ 半開区間 a なし
上に示した，閉区間 ［a,b］には最小値 a，最大値 b が存在しますが，開区間(a,b)には，最大値，最小値は存在しません。しかし，上限，下限という用語を先ほど述べたように定義しておけば，開区間(２)の下限が a，上限が b であるということができます。（部分集合Mを開区間(2)として，もう一度上限，下限の定義を読んで確かめてください。）すなわち，
下限とは最小値に，上限とは最大値に ”相当” する概念。
であることがわかります。この用語を定義しておくと，
( I ) 閉区間，開区間等に関係なく，「下限，上限はつねに存在 」し，特に，
( II ) 閉区間においては，「 M の最小値と M の下限，および，M の最大値と M の上限は一致する。」ことがわかります。
［３］ 上のM は連続した区間を想定して説明しましたが，”とびとび”の元からなる集合についても考えるときも有用です。いま，数列の第n項を，
an＝ 1 n
とすると，有限集合：
A ＝ ｛ 1 ， 1 ，･･･， 1 ｝ 1 2 N
に対しては，最大値[max]＝1，最小値［min］＝1/N，すなわち，
max A ＝ 1 ； min A ＝ 1/N
となります。しかし，n としてすべての自然数を考えた無限集合，
A* ＝ ｛ 1 ， 1 ，･･･， 1 ， ･･･｝ 1 2 n
では，max A*＝1 ； min A*＝ ”なし” というしかありません。しかし，下限と言う概念を用意しておけば，
上限： sup A* ＝ 1 ［最大値でもある］
下限： inf A* ＝ 0 ［最小値ではない］
として，集合 A* にとっての特別なカズ ”0” を一言で引用することができるのです。たいへんな優れモノですね。
［４］ 定義です。上の例では，n をずっと大きくしていくと，数列 an の第 n 項の値は 0 に近づきます。これを
an＝0
と書き，n が無限大に近づくときの an の極限は 0 であるといいます。また，このように，数列の極限がひとつの実数値であるとき，数列は収束するといいます。一方，2つの以上の値で振動したり，無限大になる場合，数列は発散すると言います。
実数の連続性の表現のいろいろ： 連続ならば，⇒
| (１)実数を上の組，下の組の２つに分けると， (１)上の組に最小値があって，下の組には最大値がない (２)下の組に最大値があって，上の組には最小値がない のどちらかだけが起こる。(デデキントの切断)
(３)ボルツァノ・ワイエルストラウスの定理 実数の有界無限集合は少なくともひとつ集積点をもつ。 ⇒ ルベーグ積分を参照 (４)コーシー列 ｛an｝
(５)区間縮小法： 数列 a1≦a2≦･･･≦an≦･･･≦bn≦･･･≦b2≦b1 のとき，ある数 c が存在して，
|
・ 2＜e＜3 の証明
・ e が超越数であることの証明
上極限 least upper bound
下極限 greatest lower bound
