ローレンツモデル 　　　　（フォノン光学モード）
f-denshi.com  更新日：
サイト検索

イオン結晶や分子性物質のような誘電体と光との相互作用を説明するための古典的モデルです。

１．ローレンツモデル

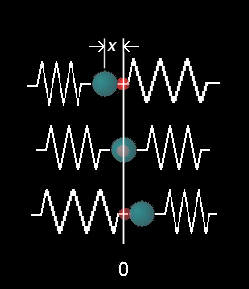
ローレンツは固体を電気双極子の集まりとして捉え，物質のもつ分散 （ ＝屈折率の波長依存性 ） をうまく説明しました。ここで，電気双極子はバネで結ばれた正負の電荷であり，運動速度に比例した抵抗を受けながら振動する調和振動子とみなされます。実際の分子では原子核の質量は電子のそれに比べてずっと大きいので，電場の変動によって位置を変異させるのは電子だけとみなした近似が許されます。

体積 V の中にある N個の調和振動子が存在し，その中で固有振動数 ω_j の割合を f_j とします。（ Σ f_j ＝1 ）

ある一つの調和振動子と光との相互作用を周期電場，

E ＝ E₀ exp（−iωt）

から受ける力の下で強制振動する電子(質量 m，電荷 e，固有振動数 ω_j ) の運動方程式は，振動の中心からの変位を x として，

m	d2x	＋ mγj	dx	＋ mωj2x ＝　eE0 exp（−iωt ）　　　･･････（１）
	dt2		dt

となります[#]。ここで，電子の運動（上式の解）も，電場と同じ振動数で周期振動すると考えられるので，x ＝ x₀ exp（−iωt ） とおき，これを（１）に代入して，振幅 x₀ を定めてやれば，

x ＝	eE0	・exp（−iωt）
	m（ωj2−ω2−ｉγjω）

となります（参考⇒[#]）。よって，固有振動数ω_j の振動子が外部電場によって誘起する分極[#]は，

Pj＝	fjNex	＝	fjNe2E0 exp（−iωt）
	V		m（ωj2−ω2−ｉγjω）V

で与えられます。これをすべての固有振動数 ω_j について合算すれば，この物質の分極が求まるはずで，

P ＝		fjNe2E0 exp（−iωt）
		m（ωj2−ω2−ｉγjω）V

と表されます。すると，複素誘電関数[#]は，

εr ＝	ε0E＋P	＝ 1＋		1	・	fjNe2
	ε0E			（ωj2−ω2−ｉγjω）		ε0mV

さらに，固有振動のうちで，特に，j ＝ 0 の場合に，　f₀　>>　f_j  と近似できるのであれば，次のパラメーター

ω → 0    のとき，　εr 　→　εr(0) ，　長波長極限 ω → ∞   のとき， εr 　→　εr(∞)，　短波長極限 ω0 ＝ ω0， γ0 ＝ γ

を用いて，

εr ＝ εr(∞) ＋	（εr(0)−εr(∞)）w2
	ω02−ω2−ｉγω

＝ε₁ ＋ i ε₂

ここで，ε_r の実数成分ε₁ を共鳴成分と呼び，電場の減衰[#]に相当する虚数成分ε₂　を吸収成分と呼びます。

と表すことができます。

以上，数式ばかりではわかりにくいので，同形の微分方程式で記述される力学のアナロジーを挙げておきます。

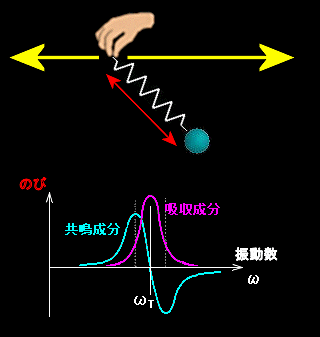ローレンツモデルの定性的な解釈 左のように重りをつるしている摩擦のあるバネの上端を左右に 振動（単振動）させた時の様子を思い浮かべてください。（左図） （１）手の動き（振動数）が小さいときは重りは常に手のほとんど真下にあり，バネもほとんど伸び縮みしません。 つまり，手から重りに力があまり伝達していないのです。これは光と物質の関係で言うと，低周波数の光と物質と相互作用が弱く，光がもっぱら物質を透過している状態に対応しています。［低周波の透過］ （２）振動数が高くなるにつれて重りの慣性によって，バネは大きく伸び縮みするようになり，手と重りの振動の位相も次第にずれていきます。これは光から物質へエネルギー移動と交換，すなわち，光の吸収や共鳴状態が生じること対応します。［光の吸収・共鳴］　 （３）さらに振動数が高くなると，手と重りがまったく正反対の動きとなり（共鳴ゼロ），バネの振幅（摩擦による発熱）は最大となります。これは最も効率よく光から物質へのエネルギー移動（光の吸収）が起きている状態に対応します。［吸収ピーク］ （４）そして，ピークを越えて，振動数が高くなると，重りは手の動きについてこれなくなり，最終的に重りはほとんど振動しなくなります。これは極めて高い周波数の光と物質とでは相互作用が再び弱くなることに対応しています。［高周波の物質透過］

したがって，複素屈折率[#]は，

n2 ＝（ε1＋		ε12＋ε22	）/ 2	［実部］

κ2 ＝（−ε1＋		ε12＋ε22	）/ 2	［虚部］

に上のε₁ とε₂ を代入して求めます。

２．量子力学的な考察

遷移確率の計算　⇒[#]

［目次へ］

εr(∞) ＋			（ω02−ω2）（εr(0)−εr(∞)）ω02	＋　i ・			γω（εr(0)−εr(∞)）ω02
			（ω02−ω2）2＋γ2ω2				（ω02−ω2）2＋γ2ω2

ε_r(0)−ε_r(∞)を用いない場合，

εr(ω)＝　1−			(ω2−ω02） ωL2	＋i ・			ω ωL2
			（ω2−ω02）2＋ω2/τ2				τ[（ω2−ω02）2＋ω2/τ2]

ただし，ωL＝		Ne2 ε0mV	，τ＝γ-1

εr(ω)実部＝　1−			(ω2−ω02） ωL2	＝　1−			((hω)2−(hω0)2)(hωL)2
			（ω2−ω02）2＋ω2/τ2				（(hω)2−((hω0)2）2＋(hω)2(h/τ)2

εr(ω)虚部＝

ω ωL2

＝

(h/τ)(hω) (hωL)2

τ[（ω2−ω02）2＋ω2/τ2]

((hω)2−(hω0)2)2＋(hω)2(h/τ)2