|
６ 熱力学第二法則 | |
| f-denshi.com ［目次へ］ 更新日： 08/04/06 最後に補足説明2-[7]以下を変更しました。 | ||
［１］ いわゆる質点系や剛体の力学には時間の方向性を示すような法則は含まれていません。それに対して熱力学では，時間の方向性を示す法則が含まれています。この熱力学第二法則と呼ばれる法則をやや哲学的に述べると，
熱力学第二法則： 熱現象は時間に対して方向性がある。
ということができます。やかんで沸かしたお湯を放置しておくと自然にさめてしまうが，その逆は起こらないということです。このような自然に進んでいく熱現象を自発変化といいます。もちろん，この表現のままでは理工学的な応用に向いていないので違った言い方･表現がなされるわけですが，特に次の４つが有名です。最初に断っておくと，これらはどれもお互い同じ内容のことをいっているのです。
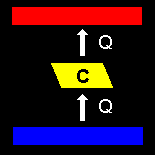
| (1) | クラウジウス (Clausius) の原理 |
他に何の痕跡も残さずに，低温から高温に熱を移すことはできない。 (やかんの水が大気の熱を自然に吸収し，熱湯となることは起こり得ません。) |
 |
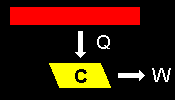
| (2) | トムソン (Tomson) の原理 |
他に何の痕跡も残さずに，ひとつの熱源から熱(＞０)を奪ってそれをすべて(外への)仕事に変えることはできない。 (これが可能ならば，周りの空気から熱を奪っていくらでもエネルギー(仕事)を取り出し，さらに冷たい冷気まで手に入ります！地球温暖化問題はすぐに解決です。) |
 |
| (3) | カラテオドリ (Caratheodory) の原理 |
すべての熱平衡状態には断熱過程では到達できない状態が存在する。(すぐ近くの状態であっても) ⇔ 外部に正の熱を放出しながら準静的過程で到達する状態には，断熱過程では到達できない。(これは難しい！)⇒ [#] |
|
| (4) | エントロピー (entropy) 増大の法則 |
系の熱力学状態が変化したときに，系が温度Tの熱源から受け取った熱量を，d'Q，エントロピー変化を
dS とすれば， d'Q ≦ TdS ( 等号は可逆な場合 ) が成り立つ。 特に孤立系( d'Q＝0 ) の状態変化においては， dS ≧ 0 |
［２］ その他よく見かける熱力学第二法則の別の表現は，
トムソンの原理(その２)
すべての仕事が熱にかわる現象は不可逆である。
カルノーの原理，
熱効率はカルノーサイクルにて最大。(T2＞Ｔ1として)
η＝ Q1＋Q2 ＝ T2−Ｔ1 ＝ 最大効率 ＜1 Q2 T2
オストワルドの原理
第二種永久機関は実現不可能
［３］ これらは，どれも証明抜きに認めるべき原理(公理)でひとつ一つに証明はありません。しかし，どれか一つを認めれば，それを用いて他の表現が成り立つことを証明することはできます。つまり，どの表現も同値であることを示すことができます。(問題によって使い分けるのです。)
［１］ 上で述べた熱力学第二法則はどれも同値であることが証明できる言いましたが，ここでは，
(2) トムソンの原理 ⇒ (4) d'Q ≦ TdS
の証明だけ行っておきましょう。
トムソンの原理(2)はもっともらしいので，「証明なしで受け入れろ」と言われれば，たいていの人は OK してくれるでしょう。しかし，フツ−の人が，「(4)不等式： d'Q≦TdS を証明なしに受け入れろ」 といわれてもそれは無理です。したがって，この⇒の証明は教育的演習という意味だけでなく，熱力学を体系に理解している感じるためには必要不可欠なのです。実際，熱力学においてこの第二法則を半定量的に取り扱う場合，このエントロピー増大の法則を示す不等式(4)から出発することになるので，この２つの表現(2)と(4)のギャップを埋めておかないとなにか気持ちの悪いものが残ってしまいます。そこで，簡潔を旨とするときわ台学でも，ここのところは省略せずにきちんと説明しておこうと思います。
ということで以下，その証明です。
ステップ1
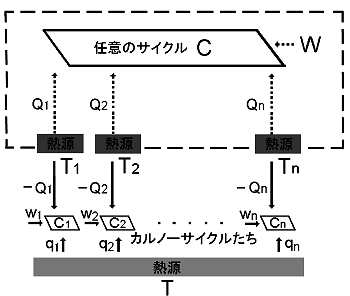［２］ まず，クラウジウス（クラジウス）の不等式を証明します。下図の黄色で示している部分だけに着目してください。必ずしも可逆とは限らないサイクルCは，
「温度が Tk (k＝1,2,･･･,n) のn個の熱源(外界)から順々に熱を受け取り，外部に仕事(-W)を行いもとの状態に戻る。 」
とします。このとき，
Qk ≦0 ［クラウジウスの不等式］ Tk
が成り立ちます。これがクラウジウス（クラジウス）の不等式と呼ばれるものです。等号は，サイクルCが可逆的な過程からなるサイクル(＝カルノーサイクル組み合わせ)であるときのみ成り立ちます。特に n＝2 の場合については前章で詳しく計算した
とおりで，
Q1 ＋ Q2 ＝0 T1 T2
を確認済みです。[#]
ここで，やや複雑なこの図の補足説明をしておいた方がよいでしょう。熱源T1,･･･,Tnの配置はサイクルCの上方に描いていますが，これは単なるレイアウトの問題であって，前章のように温度の高低の意味はありません。また，図中で，温度Tkの熱源から熱量Qkを受け取るように矢印を描いてますが，もちろんそのうちのいくつかの熱量の符号は”マイナス”，であってもよく，そのときは熱量を与えることと解釈します。仕事についてもサイクCが受け取るとき，W＞0 という符号の定義に従います。したがって，図中でサイクルCが外部に対して ”−W ” の仕事を行うと言い換えるべき場合も含めて表しています。
追加のひとこと： サイクルCは不可逆過程を含んでもかまわない という条件で考えていることは忘れてはいけません。
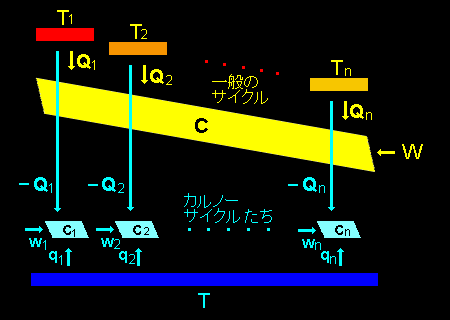［３］ さて，クラウジウスの不等式を証明するために，これからは上図の水色の過程も追加して考えます。
この水色の「サイクル過程たち」のやっていることですが，これは，「各カルノーサイクルCkは熱源Tから熱量qkを受けて，-wkの仕事を外部になし，Qkの熱量を熱源Tkに与える。」というものです。今述べた説明は図中と符号が違っているので，あれっと思ったかもしれませんが間違いではありません。「与える」⇔「受けとる」という表現はその量(仕事，熱量)の符号によって，適宜，読み替える必要がありるのは先程と同じです。また，熱源Tを図の下方に描いているのはレイアウトの都合であって，T＜Tk という意味ではないことも蛇足ながら付け加えておきます。
このような状況下で，前節の計算にならって[#]，１サイクルごとに熱力学第一法則 (これは可逆，不可逆に関係なく成り立つ！) を使うと，
サイクルC： W ＋ Qk＝0 ･･･････････(１)
サイクルCk： wk＋qk−Qk＝0 ････････････(２)
がそれぞれ成り立ちます。すべてのサイクル過程について（２）の和をとり，（１）を用いれば，
(wk＋qk−Qk)
＝ (wk＋qk)＋W＝0 ･･･････(２)'
となります。一方，各カルノーサイクルCkについて，前節で調べたように，[#]
qk ＋ -Qk ＝0 ･･････････(３) T Tk
も成り立っています。
| ［４］ 次に系全体で全サイクル C＋ |  |
Ck について考えます。 |
そのときは，熱源Tkに関しての熱のやり取り( Qkと−Qk )はキャンセルされて0 なので考える必要はなくなり，系全体で何が起こっているか( ＝サイクルCとサイクルCkが合わせてやったことは何か)といえば，
|
という サイクル過程 となっています。そこで，この系全体のサイクルに 「トムソンの原理」[#] を適用すると，この外に対して行う仕事は正であってはならないので，
−W＋ (−wk)≦0 ･･････(４)
でなければなりません。ここで，(２)'を用いると，
qk≦0 ･･････(４)'
であることがわかります。さらに(３)を用いて書き直すと，
T Qk ≦0 Tk
となります。 そして温度，T＞0 に注意して，Tで両辺割れば，上式は「 クラジウスの不等式 」[#] となります。
［５］ これが熱力学第二法則を数式化(定量化)するための足がかりです。さらにこのクラジウスの過程は連続的な極限で，
d'Q ≦0 ［ クラジウスの不等式(積分形) ］ T
と書いても構わないだろうということは，前章の２．と同じ理由です。なお，この不等式中のTは先ほどまでTk（k＝1,2,･･･）と書いていた温度の連続的な極限です。つまり，必ずしも可逆的でない一般的な状態変化が起こりながら，外界と微小な熱量d'Qをやり取りをするとき，”その瞬間”の外界温度のことです。(赤いTはここだけのサービス)
ステップ２
［６］ さて，いよいよエントロピー増大法則の証明の仕上げです。そのために 状態A から出発して，すぐ近くの 状態B を経由して，また A に戻ってくる次のサイクルを考えてみましょう。
A 任意の過程 B → ← 可逆的な過程
このサイクルにクラジウスの不等式を用いると，
d'Q ＝ d'Q ＋ d'Q ≦0 T T T
ここで，真ん中の積分の第二項は，可逆な過程 B→A なので，状態 A，B のエントロピー S(A)，S(B) の差であらわせることができます[#]。すると，
任意 d'Q ＋S(A)−S(B)≦0 ･･･ [*] T
［７］ 右図にこの不等式の熱力学的な意味を図示してみました。x-y平面上の１点は一つの熱力学(平衡)状態を表し，AとBを結ぶ曲線はAからBへの状態変化の経路のひとつを示していますが，その過程は準静的（可逆的）でも不可逆的でも構いません。また，縦軸は状態に対応するエントロピー，もしくは状態AのエントロピーS(A)＋∫（d'Q/T）です。まず，おえておかなければならないのは，エントロピーは状態量なので，平衡状態A，Bが指定されれば，どのような過程を経て，その（平衡）状態に到達したかに関わらず，それらに対応するエントロピー，S(A)，S(B)が一意的(関数S(X)は１価関数！)に定まります。図にはその点をS(A)，S(B)で示しています。不可逆過程で状態AからBへ変化した場合でも状態に１対１対応するエントロピーはS(A)から点S(B)へ移らなければいけません。
一方，図に重ね書きされている黄色，もしくは水色の曲線は，
S(A)＋ d'Q ･･･ [**] T
を状態Xについて連続的にプロットしたものです。
（独白：厳密に考えれば，AとBとが極近くにあるとはいっても有意義な差がある場合，AとBとを図のような連続曲線で結べるのは可逆な場合だけであって，不可逆過程を辿った場合は，AとBとを結ぶ熱力学平衡状態が連続的に存在してない(図の状態を表す平面状のどこにあるのか示せない)わけだから，その路を連続曲線で結んで表すこともできないはず。この図は少しインチキだと白状しておく。 が，他によい説明の図が思い浮かばない。）
まず，AからBへの状態変化が可逆的に進んだものすれば，[*]において等号が成り立つだけでなく，その途中の状態Xにおいても常に，
可逆 d'Q ＝ S(X)−S(A) T
が成り立ちます。すなわち，任意の可逆過程を考えて，この式の左辺の積分を実行すれば，状態AからXへ移行したときのエントロピー変化を正確に算出できることを意味しています。可逆過程を通してのみエントロピーを捕らえることができるということは，前章でエントロピーを定義した際にも強調したことです。このとき，
S(X)＝S(A)＋ 可逆 d'Q T
つまり，黄色の曲線は[**]の意味のみでなく，状態Xにおけるエントロピーという意味も持っています。
一方，状態AからBへの状態変化が不可逆的に進んだのであれば，
不可逆 d'Q ＜ S(B)−S(A) T
であること，すなわち，左辺の積分は，状態変化に伴うエントロピー変化よりも小さな値を算出することを意味しています。図の中でcがS(B)よりも下に書き込んであるのはこのためです。前章の最後のところで，不可逆過程で生じる熱量の出入りのようすはエントロピーの算出に役立たないと述べました[#]が，熱力学第二法則は，さらに突っ込んで，
不可逆 d'Q T
を計算すると，その値はエントロピー変化，S(B)−S(A)より小さな値を与えると述べているのです。
言うまでもありませんが，状態Aから不可逆過程で状態Bに達したときは，S(B)より小さなエントロピーをもつ点cに到達するというようなことを上の図で示しているわけはありません。エントロピーは状態量なので，系が状態Bに指定されたなら，とりうるエントロピーの値は唯一一つS(B)です。水色の曲線は，[**]を単に計算してみたに過ぎません。
［８］ ここまで述べたことを，エントロピーを主役にして言い直すと，任意の過程で，状態Aから状態Bへ変化したときのエントロピー変化，ΔSは積分，
任意の過程 d'Q T
に等しいか，より大きな値を持つ。特に，過程が断熱変化であれば，この積分は0であり，ΔS≧0 であることが言えます。この主張を孤立系に適用した，
孤立系における自発変化は，系のエントロピーを増大させる。
をエントロピー増大の法則と言います。例えば，気体が真空中へ断熱自由膨張する過程は，孤立系の自発変化とみなせるのでエントロピーの増加を伴います。これがクラジウスの不等式からわかることです。積分∫d'Q/T がゼロであることからエントロピー変化がゼロと計算することは間違いです。不可逆な過程での熱のやり取り（ゼロの場合も含む）はエントロピーの算出には役立たないのでした。
したがって，「エントロピー増大の本質を熱の移動に求めることは間違いである。」ことは統計力学を持ち出してこなくても，熱力学の範囲内で理解できることです。不可逆過程のエントロピー変化量の正しい計算は混合エントロピー[#]の計算のところで行います。
注意が一つあります。積分 ∫d'Q/T の符号については，クラジウスの不等式は何も述べていないということです。状態がAからBへ変化したとき，先ほどの図中のｃに示めす点がS(A)より小さな値をとることもあります。クラジウスの不等式から言えることは，状態変化に伴うエントロピー変化ΔSはこの積分より大きいということです。また，ΔSは積分値∫d'Q/Tより小さくならない範囲で負となることもありえるのです。つまり，説明の図で，S(B)をS(A)より上に書き込んだことも便宜的なもので，断熱変化に限らない一般的な状態変化では，S(B)をS(A)より下に書き込んでも構わないということです。もちろん，そのときc’の点はS(B)さらに下に位置します。このような状況は例えば，分子Aと分子Bが発熱反応（系が受け取る熱量はマイナス）によって結合して一つの分子Cが生成するというようなケースが挙げられます。(下図参照のこと 08/07/26 )
［９］ さて，クラジウスの不等式を認めれば，熱力学第二法則はすぐに導かれます。
| 状態変化が十分，微小であれば，エントロピーは，S(A)−S(B)＝ |  |
ｄS＝− |  |
dS と書き直してよいので， | |
d'Q − dS ＝ d'Q −dS ≦0 T T
これが任意の積分経路A→Bについて成り立つには被積分関数が常に０以下でなければならないので，
d'Q −dS≦0 T
すなわち，
d'Q≦TdS ［熱力学第二法則］
ここでの議論をまとめると，トムソンの原理を仮定し，クラジウスの不等式を導き，そこから熱力学第二法則が得られました。
CopyRight フジエダ電子出版
