Appendix １　ファンデルワールスの実在気体モデル
f-denshi.com  ［目次へ］　更新日：  08/04/04 (仮)

１．　ファンデルワールスの状態方程式　

［１］　実在気体のモデルとして，ファンデルワールス気体があります。

このファンデルワールスの状態方程式は，理想気体の状態方程式と比較して，

P^*（理想気体の圧力）　→　P＋a/v²
v^*（理想気体の体積）　→　v−b

と置き換えられています。ここで，a/v²は，

(1)　実在の分子どおしが接近したときには引力（＝ファンデルワールス力）が働く。

ということを考慮したものです。そのため実在気体で観測される圧力Pは，分子間力を考慮しない理想気体の圧力P^*に比べて小さくなるはずです。つまり，気体分子どおしが自ら集まろうとする性質のため，実在気体を閉じ込めておく外壁に及ぼす圧力(平衡条件下ではもちろん，内圧＝外圧)は理想気体に比べてa/v²だけ少なくてすむはずだということをファンデルワールスの状態方程式の圧力P＝P^*−a/v² で表しています。

一方，b は，

(2)実在の分子の体積はゼロでない大きさをもち，気体の体積に比べて無視できない。

という排除体積効果を考慮したものです。そのため，実在気体の体積vは理想気体の体積v^*よりbだけ大きくなることを，v＝v^*＋b で表しています。

［２］　さて，このファンデルワールスの状態方程式はどんな特徴を持っているのでしょうか。状態方程式[*]を陰関数として， Pv³−(bP＋RT)v²＋av−ab ＝ 0 のようにv の３次方程式に書き直してみればわかるように，関数P(v )，

P(v) ＝	RT	−	a	････････　[**]
	v−b		v2

は一般的には２つの極値，その間に１つの変曲点を持つと推察されます。しかし，

∂P	＝−	RT	＋	2a	＝ 0　　　　　･････(1)
∂v		(v−b )2		v3

∂2P	＝	2RT	−	6a	＝ 0　　　　　･････(2)
∂v2		(v−b )3		v4

を同時に満たすときは，１つの停留点をもつ減少関数となります。このとき，[**]，(1)，(2) を連立して解くと，

vc ＝3b，　Tc ＝	8a	，　Pc ＝	a
	27bR		27b2

を満足しなければなりません。この状態 (P_c,v_c,T_c) を臨界点と言います。

［３］　この臨界点を境にこの状態方程式で表される気体の性質は大きく変わります。T＞T_c であれば常に，(1)は負，(2)は正の値をとり，P(v)は下に凸である単調減少関数です。一方，T＜T_cであれば，(1)は２つの解をもちその解の間にひとつの変曲点を持ちます。この概略を図示すると右図のようになります。

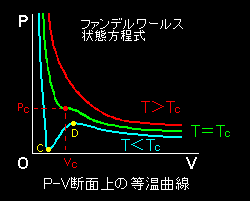
具体的な実在気体に対する a，b の値は，久保亮五編「大学演習　熱学･統計力学」（裳華房）などにあります。第27版では９ページです。

T＞T_c のとき，ファンデルワールス気体を圧縮していくと全圧力範囲で気体として振舞います。一方，T＜T_cのときは，等温曲線上の傾きが正，すなわち，

	∂P			＞ 0
	∂V		T

となっている区間CDが出現します（下図参照）。しかし，この領域に対応する状態は熱力学的に不安定であり[#]，気体は”熱平衡状態”としては存在することができません。(正確に言えば，物質の三態によらず存在し得ない。)　その意味でこの区間での状態方程式はナンセンスなわけです。しかし，まったくこのような２つの極値を示す等温曲線に熱力学的な意味を見出せないかといえば，そうではありません。この状態方程式が液体に対しても有効なことを仮定すれば，この温度領域での等温曲線は気体から液体への相転移現象を半定量的に説明できる重要な状態方程式となっているのです。

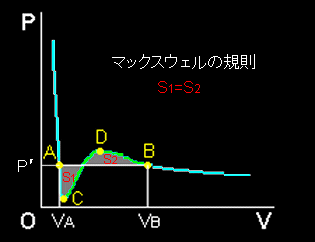
［４］　２つの極値をもつ等温曲線の解釈は，ファンデルワールス気体を体積が十分大きな状態から徐々に圧縮してゆくと，右図のBの点において液化が始まり，Bの状態の気体が消滅した分量だけAの状態に液体として出現し，この２相が共存するというものです。やや唐突にも感じられますが，当初はファンデルワールス状態方程式は液体に対しても適用可能であると考えられていたようです。

このような液化が起こる圧力P₀は次のように求めることができます。

A，Bにおける平均モルギブス自由エネルギーが等しいことから，

u_A＋P₀v_A−T₀s_A＝u_B＋P₀v_B−T₀s_B

これを書き直して，

sB−sA＝	uB−uA	＋P0	vB−vA	･･････　(4)
	T0		T0

一方，熱力学第一法則　d'Q＝du＋Pdv　を利用して，状態A→Bにそって次のような積分を実行すると，

sB−sA＝		d'Q
		T

＝		du＋Pdv
		T

＝	1		du＋	1		vB	Pdv
	T0			T0		vA

＝	uB−uA	＋	1		vB	Pdv　　　　　　　　･･････　(5)
	T0		T0		vA

(4)と(5)を比較して，

P0 (vB−vA）＝		vB	Pdv
		vA

これは図中の面積，S₁＝S₂ という幾何学的意味をもっており，マックスウェルの規則と呼ばれます。もちろん，両辺を(v_B−v_A)で除せば，液化の起こる圧力P₀が得られます。

［５］　最後にP-V図の領域A-C，B−Dについてコメントしておきます。もし，相転移を考慮しないのであれば，この領域は平衡論的には安定に存在することが可能な状態なはずです。事実，速度論的に相転移現象が追いつかないときは，この領域にある状態を観察することができるのです。たとえば,曲線B-D上の状態は過飽和蒸気と呼ばれる気体に対応すると考えます。先ほどのファンデルワールスの状態方程式の解釈によれば，気体を圧縮していってB点に到達したとき，（気体と液体のモルギブス自由エネルギーが等しくなり，）液体の生成が始まるはずです。しかし，実在の気体では気相と液相と境界には界面張力が存在し，これに打ち勝って界面を形成するための界面エネルギーが液滴の成長に必要となります。そのため，生成した液滴がまだ小さくて界面の影響が無視できないとき，液滴は速やかに成長することができないのです。したがって，液滴の成長より速く，気体状態がそのまま圧縮され，この様子が過飽和蒸気として観察されるのです。

これより，詳細な定量的な議論は二相共存平衡，界面の熱力学に譲ることとします。

［目次へ］

CopyRight　フジエダ電子出版

ファンデルワールス状態方程式のビリアル展開係数

[*]　より，

Pv ＝ RT		v	−	a
		v−b		RTv

＝ RT		1＋	-a	＋	b	＋	b2	＋	b3	＋･････
			vRT		v		v2		v3

＝ RT

1＋

b−

a

1

＋

b2

＋

b3

＋･････

RT

v

v2

v3

第２ビリアル係数：		b−	a
			RT

ビリアル展開の話はHP版では省略する。

-	熱膨張率β	等温圧縮率κ	圧力係数γp
定義	1 ∂V V ∂T P	-1 ∂V V ∂P T	∂P ∂T V
ファンデル	Rv 3Pv2−2（Pb＋RT）v＋a	（v−b）v 3Pv2−2（Pb＋RT）v＋a	R v−b

第一法則から

-	∂U ∂V T	∂U ∂P T	∂H ∂V T	∂H ∂P T
実測可能な 変数で表現	＝T ∂P −P ∂T V	＝-T ∂V −P ∂V ∂T P ∂P T	＝T ∂P ＋V ∂P ∂T V ∂V T	＝-T ∂V ＋V ∂T P
	＝Tγp−P	＝-TβV−P(-κV)	＝Tγp−1/κ	＝-TβV＋V
理想気体モデル	0	0	0	0
ファンデル

対応状態の法則

p ＝			8t	−	3
			3v − 1		v2

または，

	p＋	3		( 3v−1 ) ＝ 8t
		v2

臨界定数に

Pcvc	＝	3	＝　0.375
RTc		8

などもHP版ではパス。