| Appendix 4 電磁場の運動量 | |
| f-denshi.com [目次へ] 最終更新日: 21/10/03 むかし削除したのだが復活) | |
| サイト検索 | |
[1] マクスウェルの応力によると,物体に働く電磁気学的な力はε0μ0=1/c2として,
運動量つり合いの式
F = − ∂ (E ×H ) dV + T ・n dS ∂t c2
と書くことができました [#]。
この第2項は上で示したマクスウェルの応力ですが,第1項,
F1= − ∂ (E ×H ) dV ・・・・[*] ∂t c2
からは,ポインティングベクトルPt =(E ×H ) [#] をc2で除したベクトル(E ×H )/c2 が物質のもつ電磁場の運動量密度,または,必要範囲にわたって積分することで,この系の電磁場がもつ運動量を表すことが分かります。
[2] これは物体が静止しているときでもゼロでない「運動量」が付随することを意味しており,ニュ−トン力学において,物体の質量と速度との積で定義される運動量とは似つかない形です。しかし,符号を別にすれば,力と力学的運動量 p の満たす関係,
F = dp dt
と,[*]を比較して,(E ×H )/c2 が運動量と同じ単位をもつ物理量であることはすぐに確認できます。しかし,これだけでは(E ×H )/c2 を運動量密度と呼ぶことには抵抗があります。
そこで,この力の具体的な描像を一つ示し,ポインティングベクトルを光速の2乗で除した量,(E ×H )/c2 が電磁場に蓄えられている運動量密度にあたることを確かめてみましょう。わかりやすいように電場と磁場が直交している下図の状況で説明を行います。
[3] 原点を中心にもつ (1) yz平面内に大きな円弧を描くループには電流が流れており,その中心付近にはx方向へ向かう均一な静磁場Hが形成されているとします。また,(2) その中心付近に小さな平板コンデンサが静置されており,上部の電極が負(-Q),下部の電極が正(+Q)に帯電していることとします。電極の面積に比べて電極間の幅は十分狭く,電極の間にだけz軸正方向へ向かう一様な静電場E が形成されている(電場は電極隙間から漏れていない!) とみなせることととします。(図は見やすくするために,電流ループに対するコンデンサのサイズ,および,コンデンサの電極間距離を大きく強調して描いています。)
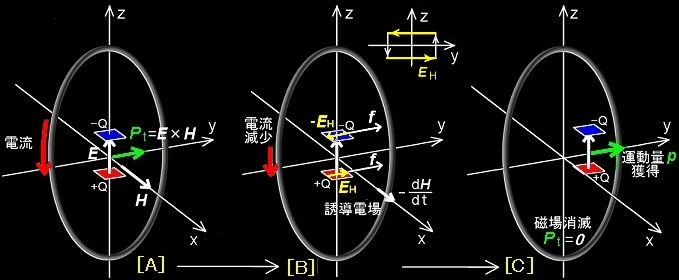
[6] この配置であるとき,ポインティングベクトルPt =(E ×H )はy軸方向を向くベクトルです [A]。この状態から外側のループに流れる電流を減少させる,,(または 0 とする)とどんな現象が観察されるでしょうか。仮に,コンデンサの代わりに,コンデンサの電極と上辺と下辺が重なるようなyz平面と平行な長方形の導体[D]が中心付近に存在すれば,レンツの法則 [#] に従い,x軸から見て反時計回り方向に電流が流れるはずです。したがって,コンデンサの置かれている空間的な対称性を考慮すれば,コンデンサの上の電極の位置には-y方向,下の電極の位置には+y方向に正味の誘導電場が形成されるはずです。
実際はコンデンサの上下の電極は分離されているので,ループ電流は流れようがなく,電荷の符号に注意すれば,上下いずれの電極もy軸正方向に力を受けることになります。つまり,外側のループ電流の減少,消滅によって,コンデンサの電極はこの力によって加速されて力学的運動量を獲得することになります。
この現象は,「電流,磁場が消失して,Pt →0 となることの引き換えとして,静止していた電極に力学的運動量 p (=Pt ) が授けられた。」と解釈することができます。これを定量的に示しているのが[*]式です。
ここで,「運動量保存則が古典力学の範囲内においてだけでなく,電磁気現象をも含めた系で成立する基本法則である」 ならば,電磁場において計算される,(E ×H )/c2 は力学的な運動量密度と等価な物理量と考えてよいでしょう。また,上で示したように質量をもつ物体の運動量と交換も可能であり,[*]式にマイナスの符号がついているのは,電磁場の運動量変化の反作用として物体が力を受けることに対応しています。