| 5 ボレル集合体 | ||
| f-denshi.com [目次へ] 最終更新日:04/11/29 | ||
| サイト検索 | ||
このページでは,ルベーグ測度を一般化するために必要なボレル集合体,σ加法族について述べます。
[1] いま,1から4までの目がでる正四面体のさいころを考えます。ここで,「
でる目 」 の集合 X を
X = {1,2,3,4}
とします。そして X すべての部分集合を元とする部分集合族 β[#],
β ={φ,{1},{2},{3},{4},
{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},
{2,3,4},{1,3,4},{1,2,4},{1,2,3},{1,2,3,4}}
を考えます。この場合,βは集合 X のべき集合 [#] β[X] でもあります。
( しかし,この言葉はあまり気にしなくても良い。 )
[2] ここで,部分集合族の任意の元 A,B について,
(1) A∈β ⇒ Ac∈β
(2) A∈β,B∈ β ⇒ A∪B ∈β
が成り立っていることは容易に確かめられます。(たとえば,A={1,2},B={1,3}とすれば,Ac={3,4},A∪B={1,2,3}も確かにβの元となっています。)これに
(0) X の部分集合をすくなくとも一つ含む。
という条件を加えた3つの条件(0),(1),(2)を満たす部分集合族を集合体,または加法族と言います。部分集合体としてはべき集合の他に,AをXの任意の部分集合とした,{φ,A,Ac,X} を選ぶこともできます(各自確認せよ)。
一般的に,条件(0),(1),(2)を満たす部分集合族は自動的に,
(4) X,φ∈β
(5) A∈β,B∈β ⇒ A∩B ∈β, A−B∈β
も満足することを示すことができます。
[3] 一方,βの元から実数への集合関数,m(A)として(もちろん,これを測度と呼んでもいい),元に含まれる目のどれかがでる確率として定義してみます。つまり,m({1,3})とは,このさいころを振って,1か3のどちらかが出る確率というように。全部書き出すと,
m(φ)=0
m({1})=m({2})=m({3})=m({4})= 1 4
m({1,2})=m{1,3}=m{1,4}=m{2,3}=m{2,4}=m{3,4}= 1 2 m({1,2,3,4}) = 1
m({1,2,3})=m{1,3,4}=m{1,2,4}=m{1,2,3}= 3 4
となります。これはもちろん,測度の条件を [#] を満足しています。さらに,有限加法性 が成り立っていることもわかります。つまり,{1},{2,3}∈β のように共通部分を持たないβの元(Xの部分集合)について,
m({1}∪{2,3})=m({1})+m({2,3})
↑123のいずれかがでる確率は1が出る確率と2か3のでる確率の和に等しい
が成り立ちます。一般化して述べれば,
A∩B=φ ⇒ m(A∪B)=m(A)+m(B)
が成り立っていることがわかります。なお,ここで取り上げた例のように,m(X)=1であるような測度を確率測度とも呼びます。
[4] このような性質が無限濃度をもつ集合 X の部分集合族について成立するとき,その集合体は,σ集合体,またはσ加法族といいます。きちんと書くと,
|
定義: 集合 X の部分集合族 β が次の3つの条件を満たすとき,σ集合体,またはσ加法族とという。特に X = Rn のときは n次元ボレル集合体と呼ぶ。
このとき,βの元 (A,Ak∈β) を可測集合といい,さらに (X,β) を可測空間という。 |
||||||
このとき,
(4) X,φ ∈ β ,φ=空集合
(5) Ak∈β(k=1,2・・・) ⇒ Ak∈β
が自動的に成り立ちます。
(4)は,A∈Xならば,Ac∈β,⇒ X=A∪Ac∈β。さらにφ=Xc∈βであるから。
(5)については,
( Ak ) c= (Ak)c ∈β
が言えるからです。
[5] または(3)の代わりに,
| (3’) A,B∈β ⇒ A∩B∈β | ||
| (3”) Ak∈β(k=1,2・・・)が互いに共通点のない集合列 ⇒ | Ak∈β | |
 を定義に用いることができます。
を定義に用いることができます。
(1),(2),(3’)+(3”) ⇒ (1),(2),(3)
を証明しておくと,
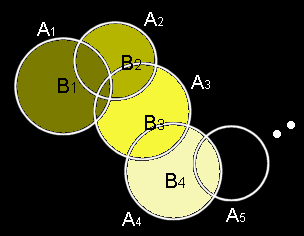
βからとった任意の集合列 {An}から右図のような
Bn ≡ An−A1∪A2∪・・・∪An-1 = An∩A1c∩A2c∩・・・∩An-1c
を作れば,(2),(3’)より,Bn∈βで各Bnは互いに共通点をもたない。さらに(3”)から,
Bk∈β
ところが,右図を見てわかるように,
Bk= Ak
結局,これは(3)が成り立つことを示している。//