| 3 ルベーグ測度と零集合 | ||
| f-denshi.com [目次へ] 最終更新日:04/10/17 | ||
| サイト検索 | ||
これまでの話から,面積をつくり出しているのはどうも有理数ではないらしいということを察っせられたのではと思います。すると,関数 f(x) の積分において,
「x=有理数 のときのf(x)の値が何であれ,それは積分に寄与しないの無視する。」
というのがルベーグ積分のポイントのように思われます。そして,そのような無視の下,それ以外のところで成り立つ事柄を,「ほとんど至るところで成り立つ」というフレーズを用いて表現します。
ところが,「有限の長さ,面積という概念を作り上げているのは無理数である。」と言い切ってしまうと,これは間違いなのです。 有理数よりも濃度が大きい無理数の集合は,面積をつくための何かを含んでいるに違いないのですが,適当に(不適切に)集めてきた,連続体濃度をもつ実数の部分集合からは有意な(>0)長さや面積は作り出せないのです。そのことを教えてくれるのが次の カントール集合 です。
[1] 次のような集合を考えます。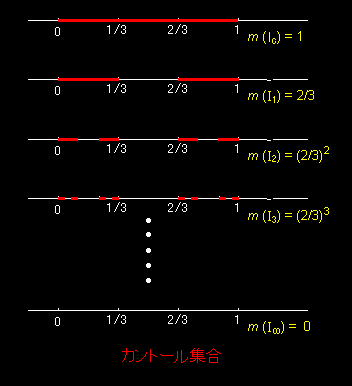
区間 I0=[0,1] から,これを3等分した真ん中の部分,すなわち,区間 (1/3,2/3)
を取り除いた残りの部分を I1 とします。
これは右図のように長さ 1/3 の2つ区間からなります。次にこの2つの区間をそれぞれ3等分して,それぞれの真ん中の部分を取り除いた部分を
I2 とします。それは右図のような長さ 1/9 の線分4つからなる区間からなります。これを
n 回繰り返すと,
In :
2n個の長さ(1/3)n の区間の寄せ集めからなる集合で測度は,
m(In)=(2/3)n
であることがわかります。
この操作を無限回繰り返したときに得られる集合 I∞ をカントール集合と言います。
[2] 3進法で表した小数,r を
r =0. a1 a2 a3 ・・・・
= a1 + a2 + a3 + ・・・ 3 32 33
と表してみれば,カントール集合とは3進法を用いて,0 と 2 とで表すことのできる実数全体の集合であることもわかります。 (右図を見てみましょう。)
このように表される集合の元の個数は,実数全体の不可算性の証明 [#] と同様に連続基数であることがわかっています。
一方,カントール集合の測度ですが,n→∞ で,m (In)=(2/3)n→0 と見積もられ,完全加法性のもとでのカントール集合の測度は 0 となります。
つまり,カントール集合は,「連続体濃度を持ち,測度がゼロである集合」 の例なのです。このように測度が 0 である集合を零集合(ゼロ集合)といいます。
可算基数をもつ有理数の集合も連続基数をもつカント−ル集合も同じ零集合として一括りにする( = そして,面積の概念作りの作業から捨て去る)ことには抵抗感がかなり感じられますが,ルベーグ積分はこのような気持ちの悪いことも礎にしていることを頭の片隅においてもらうため,零集合についてちょっと触れてみました。
[1] すでに,測度という言葉は何度も使ってきましたが,ここで正確に定義しておきましょう。とりあえず1次元 R1 で話をすると,
|
定義: ルベーグ外測度 A を実数 R上の区間 I = [ a,b ) 上の有界な集合とする。このとき,Aを完全に覆うに十分な可算個の半開区間 Ik について,
を考えて,あらゆる覆い方を考慮したときの下限,
を I のルベーグ外測度という。 |
この様子は下の図を見てもらえばわかると思います。
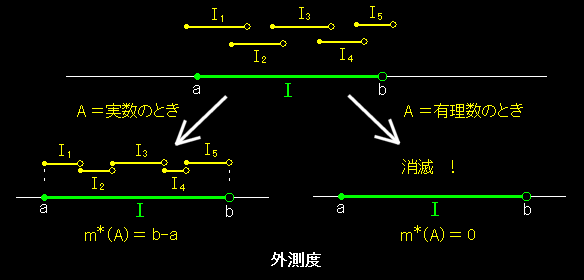
要するに A を外から(余裕をもって)囲んで,それから必要最小限のΣ|Ik| を求めることで集合 A の長さを見積もろうという作戦です。この外測度は,A
が I に含まれる実数全体
の集合であるときは直感的な長さである,b−a を与え,A が有理数の集合やカントール集合であるときは
0 となります。
可算個の Ik と言いながら,上図でたった 5個の Ik ( k = 1,2,3,4,5 )で覆っているのは,話が違うではないかと疑問に思う人もきっといることと思います。それはもっともなことで,弁明が必要でしょう。 ただし,もう少し集合論について勉強してからです。 ⇒ ハイネ・ボレルの被覆定理
|
ルベーグ外測度の性質 (1) 0≦m*(A)<∞ , (m*(φ)=0) 特に Akが互いに素なときは = が成り立つ。 このときは可算加法性が成り立つという。 |
(3)で = が成り立つ等号がなり
m*( Ak)= m*(Ak)
[2] 次はルベーグの内測度の定義。
|
定義: ルベーグ内測度 A を R上の区間 I =[a,b) の有界な集合とする。また,A の補集合を Ac とする。このとき,
を I のルベーグ内測度という。 |
ここで,
I=A∪( I ∩Ac) ← 分配法則から,
右辺=(A∪I )∩(A∪Ac)= I ∩ I = I なので,
であることに注意すれば,右辺の和集合の外測度を考えると,これは | I | より小さくはないので,
| I | ≦m*(A)+m*(I∩Ac)
つまり,
| I | −m*(I∩Ac) ≦ m*(A)
[ 内測度 ] ≦ [ 外測度 ]
という関係が成り立っています。つまり,内測度は外測度に比べて,控えめに長さを見積もっているのです。
[2-2]
|
ルベーグの内測度の性質 (1) 0≦m*(A)<∞ |
そして,m *(A) = m*(A) であるとき,これを m(A) と書いて,集合 A のルベーグ測度 といいます。
[3] これらの定義はユークリッド空間 Rn 上のルベーグ測度に拡張することができます。
n次元ユークリッド空間 Rn上のルベーグ測度の定義を示します。
|
定義: ユークリッド空間 Rn上のルベーグ測度 Rn の半開区間 J=[a1,b1)×[a2,b2)×・・・・×[an,bn) の n次元直方体 を |J|≡(b1−a1)(b2−a2)・・・・(bn−an) と定義します。 このとき J の有界な部分集合 A に対して,可算個の半開区間 Ik ; ( k=1,2,3,・・・) による被覆,すなわち,
となるようないろいろな Ik のとり方を考えて,その下限,すなわち,
をルベーグ外測度と定義する。 また, m*(A )=|J|−m*(J∩Ac) をルベーグ内測度と定義する。 さらに,A を含む任意の半開区間 J に対して, |J|=m*(A)+m*(J∩Ac) が成り立つとき,A を ルベーグ可測な集合 といい,m*(A ) を m(A) と書き,ルベーグ測度という。 |
最後のところで,1次元の場合とは違った言いまわしをしましたが,もちろん,
「ルベーグ外測度=ルベーグ内測度が成り立つとき,・・・」
としてルベーグ測度を定義しても同じです。
または,
「互いに素な任意の Akに対して,可算加法性が成り立つ。」
m*( Ak)= m*(Ak) 可算加法性
とすることもできます。
また,”ルベーグ可測な集合”を簡単に可測集合とも言います。
以上,”ディリクレ関数の積分”のエッセンスを定式化したような内容となっています。