443  球ベッセル関数
f-denshi.com  更新日：　　　22/01/13　　 サイト検索

１．球ベッセル関数

［１］　ヘルムホルツ方程式 [#] を球座標に変換した際に得られる微分方程式を考えます。

球ベッセルの微分方程式，
d2y ＋ 2 dy ＋ １− n(n＋1) y＝0
dx2 x dx x2
の2つの独立な解は、球ベッセル関数、球ノイマン関数，　［定在波］
j n(x)＝(-x)n 1 d n sinx
x dx x
および，
n n(x)＝−(-x)n 1 d n cosx
x dx x
または、球ハンケル関数　　［拡散、または収縮する球面波］
h n(1)(x)＝ j n(x)＋i n n(x) ＝−i (-x)n 1 d n ei x
x dx x
h n(2)(x)＝ j n(x)−i n n(x) ＝  i (-x)n 1 d n eｰ i x
x dx x
ここで，
h n(1) *(x)＝ h n(2)(x)

この方程式はヘルムホルツ方程式を球座標で表す [#] と得られます。たとえば、ある半径の球の内部では 0、それ以外では有限・無限大というようなポテンシャルを受けている粒子のシュレーディンガー方程式を解く際にお目にかかります[#]。

［２］　球ベッセル関数 jn(x) とベッセル関数  Jn(x) [#] との関係は、

jn(x) 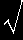＝ π ･Jn＋1/2(x)
2x
さらに、ベッセル関数の具体的な形をもちいると、
＝
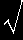π
2x
(-1)m
Γ(m＋１)Γ(n＋m＋3/2)
x n＋1/2＋2m
2
＝
π
2
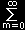(−１)m
m！(n＋m＋１/2)(n＋m−1/2)･･･(3/2)Γ(1/2)
x n＋2m
2
＝
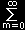(-1)m
m！(n＋m＋１/2)(n＋m−1/2)･･･(3/2)(1/2)
x n＋2m
2

ここで，ガンマ関数の計算はこちら [#] を参考にしてください。

［３］　具体的な n について、球ベッセル関数をいくつか書いておくと、

球ベッセル関数

j 0(x) ＝ sin x
x
j 1(x) ＝ 1 sin x − 1 cos x
x2 x
j 2(x) ＝ 3 − 1 sin x − 3 cos x
x3 x x2
j 3(x) ＝ 15 − 6 sin x − 15 − 1 cos x
x4 x2 x3 x
j 4(x) ＝ 105 − 45 ＋ 1 sin x − 105 − 10 cos x
x5 x3 x x4 x2
j 5(x) ＝ 945 − 420 ＋ 15 sin x − 945 − 105 ＋ 1 cos x
x6 x4 x2 x5 x3 x

球ノイマン関数

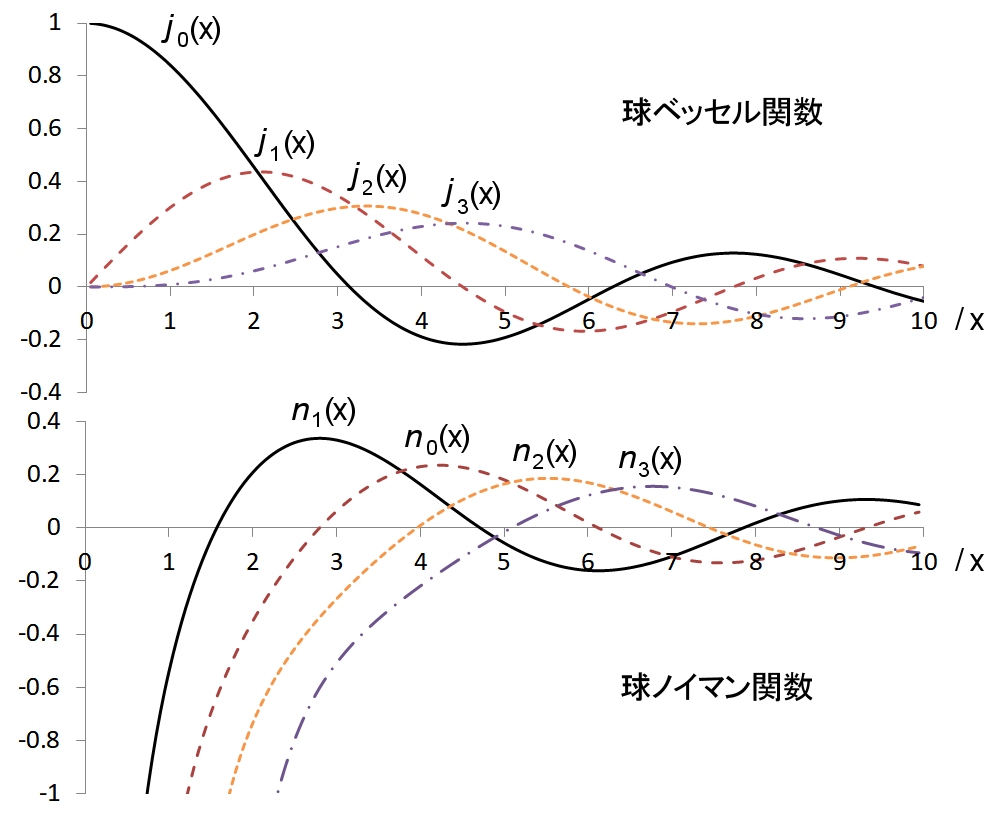
nn(x) 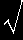＝ π ･Nn＋1/2(x)
2x
n 0(x) ＝ − cos x
x
n 1(x) ＝ − 1 cos x − 1 sin x
x2 x
n 2(x) ＝ − 3 − 1 cos x − 3 sin x
x3 x x2
n 3(x) ＝ − 15 − 6 cos x − 15 − 1 sin x
x4 x2 x3 x
n 4(x) ＝ − 105 − 45 ＋ 1 cos x − 105 − 10 sin x
x5 x3 x x4 x2
n 5(x) ＝ − 945 − 420 ＋ 15 cos x − 945 − 105 ＋ 1 sin x
x6 x4 x2 x5 x3 x


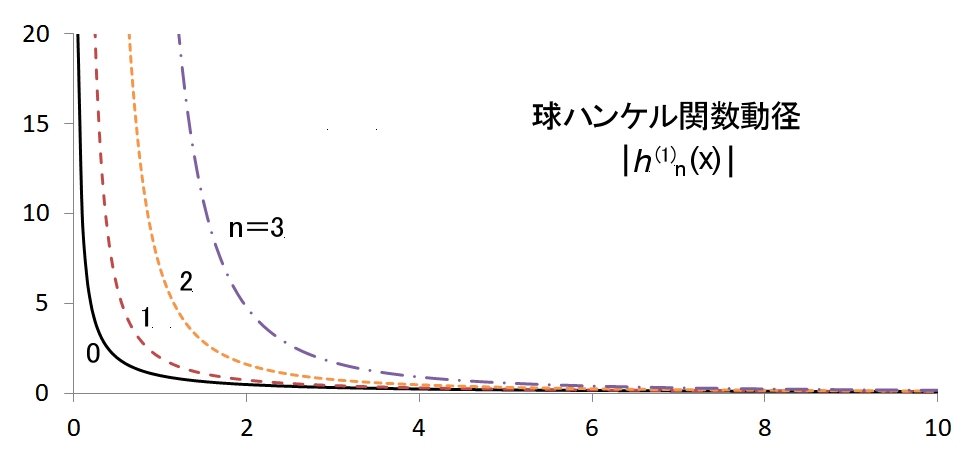
球ハンケル関数の具体形

hn(1)(x) 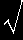＝ π ･Hn＋1/2(1)(x)
2x
h(1)0(ikx) ＝− 1  exp (ikx )
kx
h(1)1(ikx) ＝ i   1 ＋ 1 exp (ikx )
(kx)2 kx
h(1)2(ikx) ＝ 3 ＋ 3 ＋ 1 exp (ikx )
(kx)3 (kx)2 kx
h(1)3(ikx) ＝−i   15 ＋ 15 ＋ 6 ＋ 1 exp (ikx)
(kx)4 (kx)3 (kx)2 kx
h(1)4(ikx) ＝ − 105 ＋ 105 ＋ 45 ＋ 10 ＋ 1 exp (ikx)
(kx)5 (kx)4 (kx)3 (kx)2 kx
jh(1)5(ikx) ＝ i　 945 ＋ 945 ＋ 420 ＋ 105 ＋ 15 ＋ 1 exp (ikx)
(kx)6 (kx)5 (kx)4 (kx)3 (kx)2 kx


［４］　球ベッセル関数・球ハンケル関数の漸近形

漸近形 j n(x) n n(x) h(1)n(x)
x ⇒ 0
1 ・xn
(2n＋1)!!
(2n−1)!!・ -1
xn+1
-
x ⇒ ∞
1 ・cos x − (n＋1)π
x 2
1 ・sin x − nπ
x 2
1 ・sin x − (n＋1)π
x 2
-1 ・cos x − nπ
x 2
1 ・exp i x − (n＋1)π
x 2
(-i )n+1  exp (ix)
x
(2n＋1)!!  ≡ (2n＋1)(2n−1)・・・・・5・3・1




［目次へ］




j 0(x) ＝ sin x
x
n 0(x)i　＝ −i cos x
x
h 0(x) ＝ −i　 cos x
＋ sin x
x
x
h 0(ix)＝ − cos x
−i　 sin x
x
x
　　　　　＝ −
1 exp (ix)
x
j 1(x) ＝ 1 sin x − 1 cos x
x2 x
n 1(x) i　＝ − i cos x − i sin x
x2 x
h 1(x) ＝ − i ＋ 1 cos x ＋ 1 − i sin x
x2 x x2 x
h 1(ix) ＝ i ＋ i cos x − 1 ＋ 1 sin x
x2 x x2 x
　　　 ＝ i ＋ i exp ( ix )
x2 x
j 2(x) ＝ 3 − 1 sin x − 3 cos x
x3 x x2
n 2(x) i＝ − 3i − 1i cos x − 3i sin x
x3 x x2
h 2(x) ＝ − 3i ＋ 3 − 1i cos x＋ 3 − 3i − 1 sin x
x3 x2 x x3 x2 x
h 2(ix) ＝ 3 ＋ 3 ＋ 1 cos x　＋ 3i ＋ 3i ＋ i sin x
x3 x2 x x3 x2 x
＝ 3 ＋ 3 ＋ 1 exp ( kx)
x3 x2 x
j 3(x)         ＝ 15 − 6 sin x − 15 − 1 cos x
x4 x2 x3 x
n 3(x) i ＝ − 15i − 6i cos x − 15i − i sin x
x4 x2 x3 x
h 3(x) ＝ − 15i ＋ 15 − 6i − 1 cos x　＋ 15 − 15i − 6 ＋ i sin x
x4 x3 x2 x x4 x3 x2 x
h 3(ix) ＝ − 15i ＋ 15i ＋ 6i ＋ i cos x　　＋ 15 ＋ 15 ＋ 6 ＋ 1 sin x
x4 x3 x2 x x4 x3 x2 x
　　　　　　　　　＝ −i　 15 ＋ 15 ＋ 6 ＋ 1 exp(i x　)
x4 x3 x2 x
j 4(x) ＝ 105 − 45 ＋ 1 sin x − 105 − 10 cos x
x5 x3 x x4 x2
n 4(x)i　＝ − 105i − 45i ＋ i cos x − 105i − 10i sin x
x5 x3 x x4 x2
h 4(x) ＝ − 105i ＋ 105 − 45i − 10 ＋ i cos x − − 105 ＋ 105i ＋ 45 − 10i − 1 sin x
x5 x4 x3 x2 x x5 x4 x3 x2 x
h 4(ix) ＝ − 105 ＋ 105 ＋ 45 ＋ 10 ＋ 1 cos x − 105i ＋ 105i ＋ 45i ＋ 10i ＋ i sin x
x5 x4 x3 x2 x x5 x4 x3 x2 x
　　　　　　＝ − 105 ＋ 105 ＋ 45 ＋ 10 ＋ 1 exp (ix)
x5 x4 x3 x2 x
j 5(x) ＝ 945 − 420 ＋ 15 sin x − 945 − 105 ＋ 1 cos x
x6 x4 x2 x5 x3 x
n 5(x)i ＝ − 945i − 420i ＋ 15i cos x − 945i − 105i ＋ i sin x
x6 x4 x2 x5 x3 x
h 5(x)＝ − 945i ＋ 945 − 420i − 105 ＋ 15i ＋ 1 cos x − − 945 ＋ 945i ＋ 420 − 105i − 15 ＋ i sin x
x6 x5 x4 x3 x2 x x6 x5 x4 x3 x2 x
h 5(ix)＝ − − 945i − 945i − 420i − 105i − 15i − i cos x − 945 ＋ 945 ＋ 420 ＋ 105 ＋ 15 ＋ 1 sin x
x6 x5 x4 x3 x2 x x6 x5 x4 x3 x2 x
　　　　＝ i 945 ＋ 945 ＋ 420 ＋ 105 ＋ 15 ＋ 1 exp (ix)
x6 x5 x4 x3 x2 x