４　次元定理
f-denshi.com  最終更新日：03/06/27

「はじめての線形代数」PDF版がこちらからダウンロードできます。
         ⇒       　無料見本　

１．次元定理

［１］　機が熟したところで，２章の終わりに述べかけた [#] 定理を紹介しましょう。

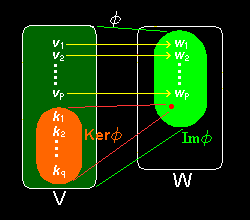
証明は，　　　　　　↓　v_j，k_j ∈ V ＝ Rⁿ，w_j ∈ W ＝ R^m，
                             φ： （ m，n ）行列 A をイメージして読みましょう。

Im φ　の基底を，　｛ w1， w2，･･･，wp ｝　つまり，dim Imφ  ＝ p Ker φ　の基底を，　｛ k1，k2，･･･，kq ｝　つまり，dim Ker φ ＝ q とするとき， 　（もちろん，φ（kj ）＝0 ，j ＝1，2，･･･，q です。） ⇒ V の基底は , 　    ｛v1，v2 ･･･，vp，k1，k2，･･･，kq ｝　　←　dimV ＝ p＋q 　 である。 ただし，v j　は，        φ（v j）＝w j　  （ j ＝1，2，･･･p ） を満たすＶに属するベクトルである。

ことを示すことで行います。　　　　

［２］　x　を任意のベクトルとすると，φ（x ）は Im φ の元なので，基底｛ w₁， w₂，･･･，w_p ｝を用いて，

φ（x ）＝λ₁w₁＋λ₂w₂＋･･･＋λ_pw_p 　　：　λ_j＝実数

とあらわせるので，次式を線形写像の性質を利用して計算すると，

φ（x −λ₁v₁−λ₂v₂− ･･ −λ_pv_p　)
                    ＝φ（x ）−λ₁φ（v₁）−λ₂φ（v₂）−･･−λ_pφ（v_p）
　　　　　　 　　 　＝φ（x ）−λ₁w₁−λ₂w₂−･･−λ_pw_p
　　　　　　　　　　＝0

したがって，

x −λ₁v₁−λ₂v₂−･･−λ_pv_p　∈ Kerφ

つまり， Ker φ　の基底，｛ k₁，k₂，･･･，k_q ｝を用いて，

      x −λ₁v₁−λ₂v₂−･･−λ_pv_p＝μ₁k₁＋μ₂k₂＋･・＋μ_qk_q 　　： μ_j＝実数
⇔
       x　＝λ₁v₁＋λ₂v₂＋･･＋λ_pv_p＋μ₁k₁＋μ₂k₂＋･・＋μ_qk_q 　　

これは，

（１）　任意のx ∈V が，v₁，v₂，･･v_p，k₁，k₂，･･，k_q の1次結合で表せる。すなわち，

｛v1，v2，･･vp，k1，k2，･･，kq ｝ がベクトル空間 V を生成する。

ことを意味します。

［３］　次に　v₁，v₂，･･v_p，k₁，k₂，･･，k_q 　が１次独立である[#]ことを示せば，これらが V の基底であることがわかりますが，そのためには，

（２）　λ₁v₁＋λ₂v₂＋･･＋λ_pv_p＋μ₁k₁＋μ₂k₂＋･・＋μ_qk_q 　＝0　　　　　　

ならば，これらの係数がすべて 0 であることを言えばいいのです。それは，

0　＝ φ（0 ）
　　＝ φ（λ₁v₁＋λ₂v₂＋･･＋λ_pv_p＋μ₁k₁＋μ₂k₂＋･・＋μ_qk_q ）
　　＝ λ₁φ（v₁）＋･･＋λ_pφ（v_p）＋μ₁φ（k₁）＋μ₂φ（k₂）＋･･＋μ_qφ（k_q）　←　φ（k_j）＝0
　　＝ λ₁φ（v₁）＋･･＋λ_pφ（v_p）＋  0　＋  0　＋･･ ＋ 0
　　＝ λ₁w₁＋･･＋λ_pw_p          ←　φ（v _j）＝w _j　  （ j ＝1，2，･･･p ）

ここで，｛ w₁， w₂，･･･，w_p ｝　は１次独立なので，上の等式が成り立つためには，λ₁，λ₂，･･，λ_p　はすべて 0 でなければいけません。これをもとの式（２）に代入すると，

（２）’　μ₁k₁＋μ₂k₂＋･＋μ_qk_q 　＝0

が成り立たなければなりません。ところが，基底，｛ k₁，k₂，･･･，k_q ｝ は１次独立なので，μ₁，μ₂，･･･，μ_q はすべて 0 でなければいけません。　結局，

（２）　ならば，λ₁＝λ₂＝･･＝λ_p＝μ₁＝μ₂＝･･･＝μ_q ＝ 0

でなければならないことがわかりました。したがって，｛ v₁，v₂，･･v_p，k₁，k₂，･･，k_q ｝ は1次独立です。そして，先程示したようにこれらは，ベクトル空間 V を生成する[#]ことと合わせると，これらベクトルの組はベクトル空間 V の基底です。 したがって，

dimV　＝　p ＋ q　＝　dim Imφ　＋　dim Ker φ

がいえました。

［目次へ］