注意: 部分モル量を表す記号として,「v~」を用いています。
| 12 2成分系の相図 | ||
| f-denshi.com [目次へ] 更新日: 08/12/15 理想的な系の議論に合わせて記号を簡略化しました。 | ||
| サイト検索 注意: 部分モル量を表す記号として,「v~」を用いています。 |
||
このページでは2成分2相共存状態の相図(または状態図)の一般式を導きます。具体的には,ある圧力P ,温度T のもとで,水とアルコールの混合溶液とそれらの混合蒸気が平衡状態として共存するようなケースが当てはまります。クラジウス-クラペイロンの式の2成分系への拡張です。
ギブスの相律[#]によれば,相の数 β=2,成分の数 r=2 のときの自由度fは,f =r+2−β= 2 です。この系の状態を記述する変数は P,T,および各相の組成を表す2つのパラメーター,例えばX相のアルコールのモル分率 x と,Y相のアルコールのモル分率 y の合計4つなので,相図は4次元空間内の曲面(2次元)で表されるはずです。
とはいってもこんな曲面の幾何学的なイメージを頭の中で思い浮かべるのは至難の業なので,この曲面を適当な2次元空間への投影図として描くことで間に合わせます。例えば2つの自由度のうち圧力Pが与えられているものとします。すると,残る変数は温度Tと各相の組成を表す2つのパラメーターx,y
の3つですが,自由度はあとひとつしか残っていないので,さらに温度Tを指定すれば,各相の組成はどちらも自動的に決まるはずです。つまり,一定圧力の下での各相の組成は温度のみの関数であり,x(T),y(T)と表すことができます。こんな関数ならば,平面上にプロットしてもその解釈は容易ですね。このx(T),y(T),またはその逆関数を重ね書きした図が相図(状態図)と呼ばれるものです。
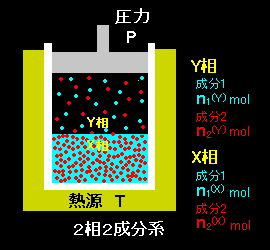
[1] それでは水を成分1,アルコールを成分2,および,液相をX相,気相をY相と一般化して話を進めましょう。2つの相に2つの成分が次の一覧表のようなモル数でそれぞれ存在し,平衡状態にある系を考えるのです。
↓↓ 下の表よーく見てください。 ↓↓
- X 相(液相) Y 相(気相) 成分1(水) n1(X) n1(Y) 成分2(アルコール) n2(X) n2(Y) ⇒
モル分率だと
- X 相(液相) Y 相(気相) 成分1 x1(X)≡x1≡1−x2 y1(Y)≡y1≡1−y2 成分2 x2(X)≡x2≡x y2(Y)≡y2≡y 系の組成を表す変数
 ここで,x1(X)+x2(X)=1, y1(Y)+y2(Y)=1であり,
ここで,x1(X)+x2(X)=1, y1(Y)+y2(Y)=1であり,
x2≡x2(X)= n2(X) [ X相の成分2のモル分率 ] n1(X)+n2(X)
y2≡y2(Y)= n2(Y) [ Y相の成分2のモル分率 ] n1(Y)+n2(Y) ↑ 組成を示す変数の主役は x2 と y2 !
が系の状態を指定する組成に関する2つの変数です。ここで,温度,圧力に関する熱平衡条件は,単一成分系の議論から推察してほぼ自明なので証明は省略して,
T(X)=T(Y)≡T (各相の温度が等しい)
P(X)=P(Y)≡P (各相の圧力が等しい)
としましょう。すると,
x2 , y2 , P, T
の4変数が指定されれば系の状態は完全に記述できることがわかります。(ただし,熱力学自由度は2です。 ⇒ギブスの相律も参照のこと[#])以下,熱平衡状態でこの4変数が満たすべき関係式を求めることになります。各成分の関わる熱平衡条件は,各相のエントロピー,体積をそれぞれ,S(X),S(Y),V(X),V(Y)として,
(δG)T,P,n1,n2=−(S(X)+S(Y))δT+(V(X)+V(Y))δP
+μ1(X)δn1(X)+μ2(X)δn2(X)+μ1(Y)δn1(Y)+μ2(Y)δn2(Y)
↓ δT=δP=0,δn1(X)+δn1(Y)=δn2(X)+δn2(Y)=0 として,
=(μ1(X)−μ1(Y))δn1(Y) + (μ2(X)−μ2(Y))δn2(Y) ≧ 0
が任意の仮想変分量δn1(Y),δn2(Y)について成立しないといけないので,
μ1(X)=μ1(Y),かつ, μ2(X)=μ2(Y) ⇒ dμ1(X)=dμ1(Y),かつ, dμ2(X)=dμ2(Y)
となります。
この2つの関係式から状態図の理論式を導出しますが,やや複雑な計算なので,とりあえずパスして,[5]の結果へ進む方が得策でしょう。
|
[2] まず,X 相のギブス-デュエムの式[#]は, GD=x1{−s~1(X)dT+v~1(X)dP−dμ1(X)} + x2{−s~2(X)dT+v~2(X)dP−dμ2(X)} =0 ・・・(1) 一方,Y 相の化学ポテンシャルの変数を T,P,y2として,成分 1,2 についての熱力学平衡条件は,
(2),(3)式を(1)に代入し,dμ1(X),dμ2(X) を消去して,
よって,変数:T,P,y2 の満たすべき(微分)方程式,
を得ます。 ただし, [3] さらに dy2の係数は等温,定圧下でのギブス-デュエムの式[#],y1dμ1(Y)+y2dμ2(Y) = 0 を用いて∂μ1(Y)を消去すれば,
となります。結局,GD = 0 は次のようになります。
[4] この方程式より, さらにここまでの導出で,X,Y相の役目を反転させると,∂x2 を含む同様な式が得られます。 以上,前ページで導いたギブス-デュエムの式が,なぜ人名が冠せられるほど重要なのか理解できたと思います。 |
[5] 2成分2相共存系の満足すべき微分方程式を一覧表にします。
| 2成分2相系の相図の理論式(一般式) | ||||||||||||||||||||||||||||||||||||||
| - | 変数を T,P,y2 ; ( y1=1−y2 ) | 変数を T,P,x2 ; ( x1=1−x2 ) | ||||||||||||||||||||||||||||||||||||
| (T-組成)曲線 |
|
|
||||||||||||||||||||||||||||||||||||
| (P-組成)曲線 |
|
|
||||||||||||||||||||||||||||||||||||
| (P-T)曲線 [2成分系のクラジウス -クラペイロンの式] |
|
|
||||||||||||||||||||||||||||||||||||
| 上式中のパラーメータの説明 | ||||||||||||||||||||||||||||||||||||||
| L(X→Y) | L(X→Y)=x1L~1+x2L~2 | L(Y→X)=−(y1L~1+y2L~2) | ||||||||||||||||||||||||||||||||||||
| L~1=h~1(Y)−h~1(X) 成分1の気化熱, L~2=h~2(Y)−h~2(X) 成分2の気化熱 | ||||||||||||||||||||||||||||||||||||||
| Δv(X→Y) | Δv(X→Y) = x1Δv~1+x2Δv~2 | Δv(Y→X) = −(y1Δv~1+y2Δv~2) | ||||||||||||||||||||||||||||||||||||
| Δv~1=v~1(Y)−v~1(X) , Δv~2=v~2(Y)−v~2(X) | ||||||||||||||||||||||||||||||||||||||
L~1は,成分1が定圧下でX 相からY 相へ微小量だけ移動するときに吸収する熱を1モル当たりに
換算した量(= 成分1の気化熱) です。L~2 も成分2に対する同様な量です。そして,L(X→Y)は,その組成におけるX 相の微小
量を十分大きなY 相へ移動するするときに吸収する熱の1モル換算値です。
一方,Δv~1 は,成分1が定圧下でX 相からY 相へ微小量だけ移動するときの体積変化を1モル当
たりに換算した量です。Δv~2 も成分2に対する同様な量で,Δv(X→Y)はその組成におけるX 相の微小量を十分大きな
Y 相へ移動するするときの体積変化の1モル換算量です。 ・・・・・ などとなります。
[1] 水(成分1)・アルコール(成分2)の2成分−気相(Y相)/液相(X相)系の相図が理論式からどのように描かれるかみてみましょう。
(1) T(x),T(y)曲線の満たすべき微分方程式は,
∂T = (y2−x2) T ∂μ2(X) = (x2−y2) T ∂μ2(X) ∂x2 P (1-x2) L(Y→X) ∂x2 T,P (1−x2)((1−y2)L~1+y2L~2) ∂x2 T,P
∂T = (x2−y2) T ∂μ2(Y) = (x2−y2) T ∂μ2(Y) ∂y2 P (1-y2) L(X→Y) ∂y2 T,P (1−y2)((1−x2)L~1+x2L~2) ∂y2 T,P
でした。これを解くために,次のような仮定を用います。(正確に言うとこの仮定は水-アルコールの系に対しては大胆すぎる!しかし成分1,2では味気ないので,引き続き水,アルコールという言葉を使わせてもらう。)
μ2(X)=定数+RTlog x2 を仮定すると ⇒ ∂μ2(X) = RT ∂x2 T,P x2
μ2(Y)=定数+RTlog y2 を仮定すると ⇒ ∂μ2(X) = RT ∂y2 T,P y2
この近似式は系が理想混合気体,理想混合溶液からなることを意味します[#]が,その詳細は後回しにして,ここでは天下り的にこれらを用いることにします。すると,
∂T = (x2−y2) RT2 ∂x2 P x2(1−x2)((1−y2)L~1+y2L~2)
∂T = (x2−y2) RT2 ∂y2 P y2(1−y2)((1−x2)L~1+x2L~2)
という連立微分方程式が得られます。この2式はたいへん重要で,この微分方程式を適切な境界条件の下で解くことによって,束一的性質と呼ばれる個々の物質の性質に依存しない物理化学的現象を説明できます。これを成分1と2の数学的対称性に注意して解くと次の結果が得られます。
(計算の詳細は⇒ PDF版 をご覧ください
|
圧力 P が与えられたときの理想的2相共存曲線
気相のアルコール(成分2)のモル分率 y2(T)≡y(T)
これらの関数を定圧条件下での2相共存曲線と言います。 また, x(T)の逆関数T(x)を液相線, y(T)の逆関数T(y)を気相線とも呼ぶので覚えておきましょう。 |
圧力 P が与えられると,2相 ( 気-液 )共存下で残る自由度は T,x,y の3つのうちの一つだけです。つまり,これらのうちどれかを定めれば残りの2つの変数の値は自動的に決まります。例えば,T=T0 と定めれば,もう自由度は残されておらず, x=x0(液相のアルコールモル分率),y=y0 (気相のアルコールモル分率)は一意的に求まります。その理論式が上の2つの2相共存曲線と関数: x(T) ,y(T) であって,各組成と温度 T との関係を,
水の沸点 T1,蒸発熱 L1 と アルコールの沸点 T2と蒸発熱 L2 ←これらは実験値を使います。
を用いて表しています。 ふつう,これらの式は縦軸(y軸)に温度T,横軸にモル分率を座標軸としてとります。つまり,逆関数:T(x),T(y) として描きます。 さらに,スペースを節約するためにこれらをひとつの図の中に各相のモル分率を共通軸(x軸)として上のようにまとめて描きます。このような図を状態図といいます。
このページで計算した最も簡単な状態図の見方を下に示しておきます。(2017/12/25追加)
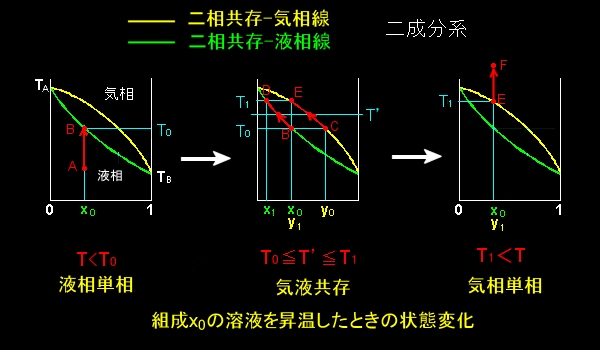 |
| 1.点Aに示す組成 x0 の溶液を加熱すると,温度 T0で液相線上の点Bとぶつかる。 2.温度T0を示す水平線は,組成 y0であるC点で気相線と交わるので,組成 x0 の液体と組成 y0の気体が平衡状態にある。 3.さらに過熱すると,温度 T’を示す直線と液相線,気相線とが交わる各点の組成の液体と気体が平衡を保ちながら, 液相はB→D,気相はC→Eと状態変化し,気化が進む。 4.温度がT1に達すると,溶液はすべて蒸発し,E点で示される組成 y1=x0 の気体となる。 5.さらに加熱すると,組成 y1=x0 の気体はE→F上で温度上昇を続ける。 |
実際の相図は理論式の導出で用いたいくつかの近似が成り立たなかったり,理想気体からのずれなどがあるためにずっと複雑な曲線となることもあります。 (実際のアルコール-水系の相図も上記のものとは少し違いますがあまり突っ込まないでくださいね) しかし,定圧下で残されている2相共存系の自由度の数は一つであることには変わりがないので,実験的に得られた相図を利用して気液共存下での残り変数を決定することはできます。ただし,実際に入手できる状態図と呼ばれる相図には,固相が関与する共存曲線もいっしょに書き込まれており,その複雑なダイアグラムを読みこなすにはそれなりの修練が必要となります。
[2] 温度を T を定めたときのP(x),P(y) は,上で,x(T),y(T)を導出したときと同様の近似に加えて,気体のモル体積>>液体のモル体積という近似を導入し,連立微分方
ひき続き,水(成分1)・アルコール(成分2) の2成分-気相(Y 相)/液相(X 相)
共存系の相図の理
論式を考察します。今度は温度をT を定めたときの圧力の組成依存性P(x), P(y)
を求めてみましょ
う。それには,先程の表に示した圧力(P). 組成曲線を決定する連立微分方程式,
∂P = (x2−y2)RT ∂μ2(X) ∂x2 T (1-x2)Δv(Y→X) ∂x2 T,P
∂P = (y2−x2) ∂μ2(Y) ∂y2 T (1-y2)Δv(X→Y) ∂y2 T,P
を解くことで求めることができます。ここでもやはり,液相,気相ともに理想的に振る舞い
|
, |
|
が成立すると仮定します。また,体積に関しては,気体のモル体積>>液体のモル体積と仮
定し,気体は理想気体の状態方程式に従い,
Δv~1=v~1(Y)−v~1(X) = v~1(Y) = RT ,および, Δv~2=v~2(Y)−v~2(X) = v~2(Y) = RT P P
Δv(X→Y) = RT ,および, Δv(Y→X) = − RT P P
と近似することにします。
[3] すると,はじめに示した連立微分方程式はそれぞれ次のようになります。
∂P = (y2−x2) P ・・・(1) ∂x2 T (1-x2)x2
∂P = (y2−x2) P ・・・(2) ∂y2 T (1-y2)y2
この2式から
∂y2 = (1-y2)y2 P ∂x2 T (1-x2)x2
これを積分して,
log (1-y2) +log a =log (1-x2) y2 x2
ただし,a = a(T) は積分定数。これをx2, y2 について解くと,
x2= y2 ・・・(3) a+(a-1)y2
y2= ax2 ・・・(4) 1+(a-1)x2
が得られます。そこで,(4) を(1) に代入して,y2 を消去すると,
dP = (a-1) dx2 P 1+(a-1)x2
これをT を定数として積分すると,
log P = log (1+(a-1)x2)+log b
∴ P(x2) = b(1+(a-1)x2) ・・・(5)
ここで,b は別の積分定数です。これに(3) を代入して変数をy2 とすれば,
P(y2) = ab ・・・(6) a+(1-a)y2
も得られます。これらが圧力-組成曲線を与える式です。残されたことは2つの積分定数を決める
ことです。それにはまず,(5) において,温度T の下でx2 = 0 としたものは,純粋な成分1が
温度T の下で2相平衡状態にあるときの飽和蒸気圧P1 でなければいけません。すなわち,
P (x2 = 0) = b = P1
と決められます。今度は,x2 = 1 としたときの圧力を考えると,それは純粋な成分2が温度T の
下で2相平衡状態にあるときの飽和蒸気圧P2 でなければいけません。これより,
P (x2 = 1) = ab = P2
結局,積分定数は,
a =P2/P1 ,b = P1
と定めることができます。これを(5),(6) 式に代入すれば,
P (x2) = P1(1+(P2/P1−1)x2 )= P1+(P2−P1)x2
P (y2) = P2 = P1P2 P2/P1+(1−P2/P1)y2 P2+(P1−P2)y2
となります。
[4] 以上をまとめると,下図のようになります。
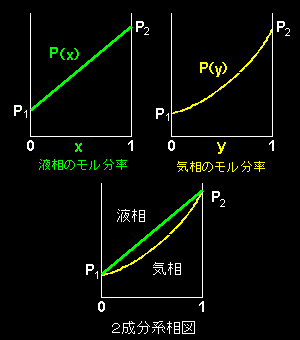
温度 T が与えられたときの理想的2相共存曲線: 温度 T において気-液共存平衡にある純成分1の圧力(飽和蒸気圧)を P1,純成分2の圧力(飽和蒸気圧)を P2 として, 液相の成分2のモル分率 x に対する共存曲線 P(x)= P1+(P2−P1)x 気相の成分2のモル分率 y に対する共存曲線
これらの関数を定温条件下での2相共存曲線と言います。 |
[5] ところで,このP-組成図の液相線を,x1=1−x2 を用いて,書き直すと,
P (x2) = P1+(P2−P1)x2=x1P1+x2P2
と書き直すことができます。気相の圧力が成分1と2の各分圧の和で表されると考えるとき,
成分1の分圧: p1=x1P1
成分2の分圧: p2=x2P2
とみなすことができます。すなわち,
「気相の各成分の分圧は,各成分の液相のモル分率とその純粋成分の飽和蒸気圧との積に等しい。」
と述べることができます。これをラウール の法則 (Raoult's law) と言い,3成分以上の不均一系についても成り立ちます。
不均一平衡系の自由度についてはギブスの相律と呼ばれる公式があります。それは系が r個の成分からなり,β個の相が共存している場合,この系の自由度は,
f = r + 2 − β (自由度) (成分の数) (相の数)
で与えられるというものです。以下証明です。
変数の個数は不均一系の各相 X ごとに,
x1(X),x2(X),・・・,xr-1(X),P(X),T(X)
の r+1 個です。( xr(x)については,1−(x1(X)+x2(X)+・・・+xr-1(X))より自動的に定まるので考える必要はない。)したがって,β個のすべて相について合計すると,
(r+1)β [変数の数]
一方,この不均一平衡の条件となるその方程式の数は,まず,各成分 j ごとに,
μj(1)=μj(2)=・・・・・=μj(β)
のβ−1個あるので,r個の全成分では,r(β−1) 個となります。さらに,温度,圧力についても,
P(1)=P(2)=・・・・・=P(β)
T(1)=T(2)=・・・・・=T(β)
の2(β−1)個の方程式が作れます。したがって,方程式の総数は,
(r+2)(β−1) [方程式の数]
となります。したがって,
(連立方程式の解空間の次元) = (変数の数)−(方程式の数)
= (r+1)β−(r+2)(β−1)
= r+2−β
がこの不均一系の自由度f となります。
ギブスの相律2: 別の数え方 (示強変数の微分量を考える)
各相 (X=1,・・・,β) について,ギブス-デュエムの式[#],
x1(X){−s~1(X)dT(X)+v~1(X)dP(X)−dμ1(X)}+・・・+xr(X){−s~r(X)dT(X)+v~r(X)dP(X)−dμr(X)}= 0 [*]
が成立します。不均一平衡条件は,
dP(1) =dP(2) =・・・・・=dP(β) ≡dP
dT(1) =dT(2) =・・・・・=dT(β) ≡dT
dμ1(1)=dμ1(2)=・・・・・=dμ1(β)≡dμ1
:
dμr(1)=dμr(2)=・・・・・=dμr(β)≡dμr
となります。これをギブス-デュエムの式[*]に代入すると,
x1(X){−s~1(X)dT+v~1(X)dP−dμ1}+・・・+xr(X){−s~r(X)dT+v~r(X)dP−dμr}= 0 ( X=1,・・・,β)
という微分方程式がβ個得られますが,ここで残った変数は,dμ1,・・・,dμr,dP,dT の r+2 個です。したがって,変数の数から方程式の数を引いた, r+2−β がこの不均一平衡系の自由度です。
具体例を示しておきます。本文中で扱った2相2成分系では,
変数4つ: dμ1,dμ2,dP,dT
方程式2つ: x1(X){−s~1(X)dT+v~1(X)dP−dμ1} + x2(X){−s~2(X)dT+v~2(X)dP−dμ2} =0
x1(Y){−s~1(Y)dT+v~1(Y)dP−dμ1} + x2(Y){−s~2(Y)dT+v~2(Y)dP−dμ2} =0
となっているので自由度は2となります。本文中では,dP=0 とするなど自由度をその都度制限し,変数の数を3つ,自由度を1に減らして議論しています。
| 成分の数 | 相の数 | 自由度 |
| 1 | 1 | 2 |
| 1 | 2 | 1 |
| 1 | 3 | 0 |
| 2 | 1 | 3 |
| 2 | 2 | 2 |
| 2 | 3 | 1 |
| 3 | 1 | 4 |
| 3 | 2 | 3 |
| 3 | 3 | 2 |