|
５ ハミルトン方程式 |
| f-denshi.com 最終更新日： 03/03/18 | |
| サイト検索 | |
解析力学ではラグラジュ関数とハミルトニン関数の使い分けが一つのポイントです。これら相互の変換はその部分の数式だけフォローしようとすると何のために何をしようとしているのか？ということになりがちです。しかし，ここで使われる数学的な技巧はルジャンドル変換と言われる対称性を持っています。
［１］ 独立変数が２つである，3変数(x，y，v)−2関数(φ，λ)のルジャンドル変換を下に示します。これらの導出はときわ台学「実数解析入門」⇒[#]を参照して下さい。
φ(x，y) λ(x，v) φ＝λ＋yv λ＝φ−yv， dφ＝udx＋vdy dλ＝udx−ydv
u＝ ∂φ y：v＝ ∂φ x ∂x ∂y
u＝ ∂λ v：−y＝ ∂λ ｘ ∂x ∂v
ラグランジアンと(符号を換えた)ハミルトニアンの関係
−H(q，p)＝L(q，q’)−q’p ⇒３次元とき， −H(q，p)＝L(q，q’)−q’･p ･････ [*]
もルジャンドル変換 (変数の一部の置換：q’→p ) の関係にあります。
［２］ 実際，上の表で，
x → q， y → q’， v → p，；
φ → L， λ → −H
と置き換えると，
L(q，q’) -H(q，p) L＝-H＋q’p −H＝L−q’p dL＝udq＋pdq’ −dH＝udq−q’dp
u＝ ∂L q’：p＝ ∂L q ∂q ∂q’
u＝ ∂(-H) p：-q’＝ ∂(-H) q ∂q ∂p
∂L − d ∂L ＝0 ただし，q’＝ dq ∂q dt ∂q’ dt
を使えば，表の赤ワクのu＝･･ の等式は，
u＝ ∂L q’＝ d ∂L q ＝ dp ＝ｐ’ ∂q dt ∂q’ dt
と変数 p で表せます。↑最後の”＝”は，同じ赤いセルの右の等式：p＝(∂L/∂q’)qを使いました。
ここで，q’ は１．で述べた一般化座標の時間微分ですが，ルジャンドル変換後に対応する変数p を一般化運動量と呼びます。きちんと書くと，
定義：
p＝ ∂L q [一般化運動量] ∂q’
１章で考えたような簡単な系：L＝（1/2)･mv2−（−G0mM/x) の場合は，ニュートン力学で定義される運動量，mq’ と一般化運動量は一致しますが，ローレンツ変換を内包する電磁気現象[#]が関係するときはニュートン力学における意味と異なってきます[#]。量子力学において運動量というときはこの一般化運動量のことを指します。ここに定義した一般化運動量は，そのような意味で座標系に依存せず，”真の運動量”ということができます。
［３］ したがって，E-L方程式と L のルジャンドル変換から，
dp ＝ ∂L q’ ： p＝ ∂L q dt ∂q ∂q’
及び，関数としてH を用いた(右側の黄ワクより)，ハミルトン方程式，または，ハミルトンの正準方程式 と呼ばれる，
(p’＝) dp ＝− ∂H p ： (q’＝) dq ＝ ∂H q ［ハミルトンの正準方程式］ dt ∂q dt ∂p
が得られます。
［４］ ラグラジアン(Ｌ)を使った表現［ ラグランジュ方程式 ］とハミルトニアン(H)を使った表現［ ハミルトン方程式 ］との違いを一言で言うならば，力学を記述に用いる変数として，位置q ともう一つの変数として，
「(１)q の微分q’を使う(L)のか，それと同等な(２)変数p を使う(H)のか 」
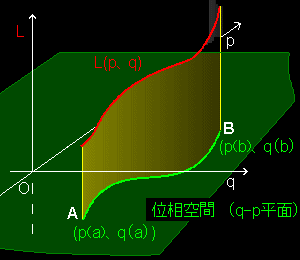
の違いです。数学者から見れば，L と q，q’ を使う方が，「汎関数の極値という数学的な意味が明解」でスッキリしているのでしょうが，物理学者から見れば，q’のような変数より，ニュートンの偉大な業績である運動量と結びつくp をエネルギーに相当するハミルトニアンH といっしょに扱う方が直感的に把握できてよい！という感じなのでしょうか？．．．もちろん，(q，p)を２次元平面にプロットした位相空間の有用性も重要です。
［１］ 変分原理に従って直接ハミルトンの正準方程式を導くともできることも指摘しておきましょう。その場合，
L(q，q’) ⇒ L(t，q，p)＝p･ dq −H(q，p)
dt
のように L では独立変数がq，p であると考えて，作用積分
S[q(t)，p(t)]＝ L［t，q(t)，p(t)］dt
を最小とするようなA からB への積分経路を変分法に従って求めることになります。 ⇒ [#]
［６］ ここでは，各変数が３次元の場合を物理の本でよく見られる第一変分を求める記述法[#]を使ってみましょう。
(δq(a)＝δp(a)＝0，δq(b)＝δp(b)＝0 )
δS[q(t)，p(t)] ＝δ L［t，q(t)，p(t)］dt
＝δ p･ dq −H(q，p)
dt
dt ↓ 第２項部分積分。 (∇qH)はH をq のベクトル値関数とみたてた勾配，(∇pH)はH をp のベクトル値関数とみたてた勾配。
＝ δp･ dq ＋p･
dδq −(∇qH)δq−(∇pH)δp
dt dt dt ↓固定端条件ではδq(a)＝δq(b)＝0なので，
＝［p ･δq ］ ＋ δp ･ dq ＋δq ･
dp −(∇qH)δq−(∇pH)δp
dt dt dt
＝ dq −(∇pH) δp − dp ＋(∇qH) δq
dt dt dt
q，p が独立変数なので，これが常に成り立つ条件は，
dq −(∇pH) ＝0 かつ， dp ＋(∇qH) ＝0 dt dt
成分で表すと，
３次元空間 (６次元位相空間[q，p] )でのハミルトン方程式は，
の６個の方程式。 |
結局，どの変数についても同じ形の方程式なので，EL方程式と同じように一般化座標，一般化運動量を用いて一組(２つ)の方程式を扱えば十分であることがわかります。
つづく ････
(注意)スカラー関数H(x，y，z)についての全微分公式：
dH ＝ ∂H dx＋ ∂H dy＋ ∂H3 dz ＝(∇H)･dr ∂x ∂y ∂x
ただし，dr ＝(dx，dy，dz)，
∇H についてはこちら→[#]
