| 3 自由群と基本群 | ||
| f-denshi.com [目次へ] 最終更新日:23/11/02 加筆 | ||
| サイト検索 | ||
ときわ台学の「代数学入門」の第1部 群 を既読として解説します。
[1] 自由群とは,群の定義を満足する以外は"元"どおしの間に条件が課せられていない群ということができます。
まず,群の定義を代数学入門から再掲載しておくと,
群の定義
集合Gに属する順序のついた任意の2つの元(a,b)を(←(a、b)と(b、a)とは識別可能と言う意味)、集合 G に属する一つの元 c に対応させる規則があるとき、集合 G に演算が定義されているといい、この対応: (a,b) → c を
a・b=c
と書くことにします。この集合 G と演算 ・ が次の3つの条件を満たすとき、集合 G は演算 ・ について群をなすといい、群(G、・ ) または簡単に 群G と書きます。
| 群の定義
(1)[結合法則] (2)[単位元の存在] (3)[逆元の存在] 上の定義から,e・a=a,および,b・a=e も自動的に満たされる。 |
ここで(2)における e を単位元という。
また、(3)における b はa の逆元といい、a の逆元であることを強調するために、a-1 とも書く。
[2] 最も簡単なのは,単位元だけから生成される自明群 G={e} ですが,これは面白くないので,群が e の他に a≠e を含む群を考えてみます。
群の定義からその逆元 a-1 も当然含まれることになります。さらに,a または a-1 どおしの演算を繰り返した結果に結合法則を考慮すれば,
a,aa,aaa,・・・ (aの個数>a-1の個数のとき)
a-1,a-1a-1,a-1a-1a-1,・・・ (a-1の個数>aの個数のとき)
e (a-1の個数=aの個数のとき)
(演算(積)記号 ・ を省略した)
がそのまま形で自由群G の元となっていなければなりません。 これらの元は,a を文字とする 語と呼ばれます。なお,語は a … a (←aがp個) は ap のように書くこともあります。
この群の元として,aとa-1が混じり合った語は含ませる必要はありません。なぜなら,aa-1=e,ex=xe=x (x=aまたはa-1) となるので,語に含まれる a か a-1かどちらかその個数が少ない方は消し去ることができるからです。例えば,
a-1aaa a-1= (a-1a)a(a a-1) = eae = a
のように。このようにして ”消し去る操作” を簡約といいます。また,それ以上簡約することのできない語を既約な語といいます。既約な語だけを用いて,この自由群の元の集合は,
F(a)={e,a,aa,aaa,・・・,e,a-1,a-1a-1,a-1a-1a-1,・・・}
と書くことができます。これを生成元を a とする無限巡回群といいます。
容易に分かるように,F(a) は可換群であり,整数加群(Z,+)と
ap ⇔ p∈Z f(p)=ap (元の対応)
・ ⇔ + (演算の対応)
と対応させれば,
m + n = (m+n)
↓ ↓ ↓ f(m+n)=am+n=am・an=f(m)+f(n)
am・an = am+n
は全単射準同型写像なので,F(a) は整数加群と同型です。
F(a) 〜 Z 整数加群
[3] 自由群として文字が一つだけではなく,2つ,a,b を含む場合を考えることができます。
a,b を文字とする語の場合は aとa-1とだけでなく,bとb-1がとなり合わせの場合も簡約ができます。また,単位元 e は a, b どちらの生成元に対しても ae=a,be=b です。 a,b を文字とする自由群は F(a,b) と書きます。
[4] 一般に n 個の生成元を含む自由群を考えることができます。その定義を示しておきます。
|
定義 階数nの自由群 相異なる a1,a2,・・・,an,および,a1-1,a2-1,・・・,an-1 を文字とする語の全体集合に対して,語と語を並べて繋ぎ新しい語とする演算と,規約:akak-1=e (k=1,2,…,) が与えられているとき,これを階数nの自由群といい, F(a1,a2,・・・,an ) と表す。 |
有限回の繰り返しの演算に対して結合法則が成り立つことは自明です。
任意の2つの自由群から新たに自由群を作り出すことを考えます。
|
定義 自由積 任意の群G と H の元を(文字とみなして)適当に取り出した並びを語とする。そのとき,同じ群から取り出した元が並んでいれば,その群の演算を行い,それをその群の一つの元(一文字)とみなすこととする。そのようにして作られる語全体は,並べて繋げるという演算の下で群をなすが,これを 群 G と H の自由積といい, G*H と表す。 特に,自由群どおしの場合, G=F(a1,a2,・・・,an) であれば,これらの自由積は, G*H=F(a1,a2,・・・,an,b1,b2,・・・,bn)のことである。 |
例として,2つの可換群(加群) G=F(a) 〜 Z,H=F(b)〜Z を考えます。m1,m2,・・・∈F(a),n1,n2,・・・∈F(b) とすれば,自由積 G*H の元は形式的な和の記号+を用いて,
・・・+mi+nj+mk+nl+・・・ 有限個の和
のような形で,F(a) と F (b) に属する元が交互に並んた形式で表されます。
[6] 自由群は生成元を並べることで群を表すこと,すなわち群の表示とすることができますが,一般的な群の表示は生成元と生成元に課せられる条件を並べて群を表現することになります。 それを保証するのが次の定理です。
|
定理 G を生成元 g1,g2,・・・,gn によって有限生成される群とする。このとき,自由群 F(a1,a2,・・・,an)から群Gへの写像を f(ak)=gk と定めれば,これは全準同型写像となる。したがって,準同型定理によって, G = F(a1,a2,・・・,an) / Ker f と表される。
特に F(a1,a2,・・・,an) の正規部分群である Ker f が有限個の H=( h1,h2,・・・,hm ) ,hk∈F(a) (k=1,2,…,m) で生成されるならば, 群G は自由群の剰余群として次のように表すことができる。 G= F(a1,a2,・・・,an)/( h1,h2,・・・,hm ) これは,自由群 F の生成元に対して,h1=e,h2=e,・・・,hm=e という関係を定めることに等しく,関係子と呼び,巡回群の表記を用いて, <g1,g2,・・・,gn>=<a1,a2,・・・,an|h1=e,h2=e,・・・,hm=e>と表すことができる。これを群Gの表示という。 |
補足:
定理中の”正規部分群”の元を列挙すれば,{ x-1hkx },(k=1,2,…,m),x∈F(a) となるが,これを( h1,h2,・・・,hm )という記号で表している。具体例を見た方が分かりやすいので,ここで分からなくても先へ読み進むべし。
[7] 具体例をみてみましょう。
例1
群G として,生成元がg,位数が6の巡回群 Z6 [#] を考えてみます。生成元だけで表記すると,
Z6 = { e', g, gg, ggg, gggg, ggggg, }, ただし,e'=gggggg
となります。e' はこの群の単位元で,gp の逆元は g6-p です。ここで,自由群 F1(a) から Z6 への写像 f を a を g に対応させる写像とすると,すなわち,
f(a)=g,f(aa)=gg,…,f(aaaaa)=ggggg,f(a-1)=g-1,・・・
とすると,
f(aa)=gg=f(a)f(a), f(e)=f(aa-1)=f(a)f(a-1)=gg-1=e'
などが確かめられて f は上への準同型写像と分かります。また,
Ker f = f-1(e')={ x-1・a6・x|x∈F(a) } ≡ (a6)
となっています。したがって,準同型定理より,
Z6 〜 F1(a) / (a6)
= { e ,a,aa,aaa,aaaa,aaaaa }
であり,生成元と関係子を用いて,
<g> 〜 <a|a6=e>
と表すことができます。
[8]
例2
3文字の対称群,
S3={ e',τ1,τ2,σ1,σ2,σ3 }
を考えます。群表と元である置換を以下に示します。
* e' τ1 τ2 σ1 σ2 σ3 e' e' τ1 τ2 σ1 σ2 σ3 τ1 τ1 τ2 e' σ2 σ3 σ1 τ2 τ2 e' τ1 σ3 σ1 σ2 σ1 σ1 σ3 σ2 e' τ2 τ1 σ2 σ2 σ1 σ3 τ1 e' τ2 σ3 σ3 σ2 σ1 τ2 τ1 e'
|
|
|
|||||||||||||||||
|
|
|
これらの積をいくつか抜き出すと,
σ1σ1=σ2σ2=e'
σ1σ2=τ2
σ2σ1=τ1
σ2σ1σ2=σ1σ2σ1=σ3
であるから,S3の生成元として,σ1,σ2 を選べることが分かる。
S3を生成元だけで表すと,
S3={ e',σ2σ1,σ1σ2,σ1,σ2,σ1σ2σ1}
したがって,自由群 F(a,b) から S3 への準同型写像 f として,
f(a)=σ1,f(b)=σ2
を定めて,Ker f として,
f(aa)=σ1σ1=e'
f(bb)=σ2σ2=e'
また,
σ3σ3=(σ1σ2σ1)( σ2σ1σ2)=(σ1σ2)3=e'
なので,
f((ab)3)=(σ1σ2)3=e'
を見出せる。残りの単位元 e' を与える S3の元の積は,
τ1τ2=σ2σ1σ1σ2=e'
τ2τ1=σ1σ2σ2σ1=e'
ee=e
であるが,すでに求めた関係子から自動的に成立するので,結局,f(a,b)の正規部分群はその生成元を用いて,
Ker f =( aa,bb,(ab)3 )
とすれば必要十分であることが分かります。
準同型定理より,
S3 ={ e,σ2σ1,σ1σ2,σ1,σ2,σ1σ2σ1}
〜 F(a,b)/( aa,bb,(ab)3 )
={ e,ba,ab,a,b,aba }
生成元と関係子を用いて表すと表すと,
S3=<σ1,σ2> 〜 <a,b|aa=e,bb=e,(ab)3=e>
さて,2つの可換群(加群) G=F(a) 〜 Z,H=F(b)〜Z を考えます。
ここで,m1,m2,・・・∈F(a),n1,n2,・・・∈F(b) とすれば,自由積 G*H の元として,
・・・+mi+nj+mk+nl+・・・ 有限個の和
を考えると,これ以上は簡潔に表せません。
しかし,F(a) の元と F(b) の元が可換である,すなわち,ab=ba が成り立つのであれば,
・・・+mi+nj+mk+nl+・・・
=(…+mi+mk+…)+(…+nj+nl+…) = m+n
ただし,m=…+mi+mk+…, n=…+nj+nl+…, m∈F(a),n∈F(b)
のように F(a) の元と F(b) の元をそれぞれ一か所にまとめて直和加群,
GH = F(a)
F(b) 〜 Z
Z
として表すこととができます。これを自由積 G*H の可換化といいます。
直和加群についてはこちらのページを参考にしてください ⇒ [#] 。
[10]
例3 対称群 S3の可換化
S3 =<a,b|aa=e,bb=e,(ab)3=e>
を可換化するためには,関係子に ab=ba を追加すればよい。すると,それは,
(ab)3=e ⇒ a3b3=e ⇔ a(a2b2)b=e
⇔ ab=e ⇔ b=a-1
の関係を導入すること相当する。すなわち,対称群 S3の可換化は,
[S3]/[S3,S3] =<a|aa=e>〜 Z2 (位数2の巡回群)
となります。
ここで,[S3,S3] は交換子群で,群Gの可換化を [G]/[G,G] と表記することができます。その正当性については,当ホームページの代数入門 「10-2 交換子群と可解群」 を参考にしてください。
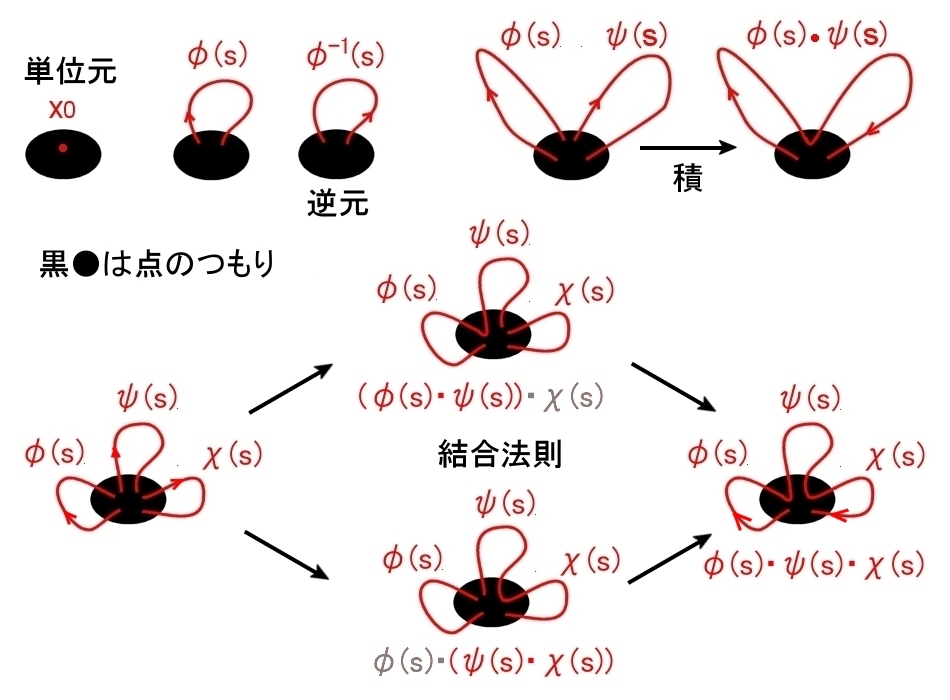
[1] 弧状連結な図形 (=位相空間としてもよいがここでは具体的な図形のイメージで説明する) X の基点と呼ばれる一点から出発して,同じ点に戻る連続曲線 (連続写像) φ:[0,1]→X,φ(0)=φ(1)=x0 をループといいます。
ホモトープ とは,連続的な変化で写りあえる2つのループの関係のことで,形式的に述べると,
|
定義 ループφとψがホモトープ 弧状連結な図形 X における点 x0 を基点とする2つのループ φ0(s) とφ1(s) : [0,1] → X がホモトープであるとは,連続写像, H(t,s) : [0,1]×[0,1] → X が存在して,(s はループを表すのパラメータ,t はループの変形を表すパラメータ) (1) H(0,s)=φ0(s) かつ, を満たしていることである。 ここで,連続写像 H(t,s) をφ0からφ1へのホモトピーと呼ぶ。また,ループφ0とφ1がホモトープであることを φ0〜φ1 と書く。 |
X の中に基点を一つ固定してすべてのループを考えるとき,ホモトープは同値関係〜を与えます。
すなわち,
(1) φ〜φ
(2) φ〜ψ ⇒ ψ〜φ
(3) φ〜ψ, ψ〜χ ⇒ φ〜χ
を示すことができます。その同値類の一つ一つをホモトピー類 [φk] と呼びます。(φkは代表元)
また,ホモトピー類の全体集合を,π1(X,x0) と書きます。
π1(X,x0)={ [φ1], [φ2],・・・, [φk],・・・ }
このとき,π1(X,x0) には群の構造を入れることができます。
ここでは,[φk] と表していますが,文脈からホモトピー類であることが自明の場合は,[ ] をはずして,φk と書くこともあります。
[2]
|
基本群の定義 (1次ホモトピー群ともいう。) 元 : ホモトピー類 [φk] その全体集合, π1(X,x0)={ [φ1], [φ2],・・・, [φk],・・・ } は以下の演算に関して群をなす。その群も同じ記号 π1(X,x0) で表す。 積 (演算): ループを繋ぐことで,
に対応させて,積は, [φk]・[φj]≡[φk・φj] とする。 ( 「・」は省略することもある。「・」は代表元どおしを繋ぐこと ) 単位元: x0から動かないループ x0^ のこと。このホモトピー類 [x0^] を [e] と表す。 逆元 : φk と逆向きに進むループ φk-1(s)≡φk(1−s) の属するホモトピー類 [φk-1] これを [φk]-1 と表す。 結合法則: ([φi]・[φk])・[φj]=[φi]・([φk]・[φj]) |
例
例として,円周S1の基本群をあげておきます。
簡単な説明
x0 を円周の任意の点として,x0 から出発して定められた円周の順方向に1周だけしてx0 に戻るループが生成元です。すると,円周を何周してx0に戻ってくるかによってループを特徴付けることができます。そのとき,逆方向に回るループにはマイナスを付け,x0 にとどまって動かないループ,単位元は0周したループと考えます。つまり,ループは,
Z={ ・・・,-2,-1,0,1,2,・・・ } 整数の加法群
と1対1に対応させることができて,演算は,通常の加法に対応します。すなわち,
π1(S1,x0) 〜 Z 〜 F(α) (整数加群)
ということができます。
厳密な証明
は長過ぎるので,欄外にスキームだけ示しておきます。⇒ こちら[#]
なお,単位元だけからなる最も単純な基本群をもつ図形には名前が付いています。
|
定義 π(X,x0)={ e } である弧状連結な図形 X を単連結な図形という。 |
例
2次元球面 S2,2次元円板 Δ2 は単連結な図形である。
[4]
|
定義 連続写像φとψが基点を保ったままホモトープ 弧状連結な位相空間 X ,Y それぞれの基点を x0 ,y0 とする。このとき,連続写像, φ0(x),φ1(x) : X → Y が基点を保ったままホモトープであるとは,連続写像, H(t,x) : [0,1] × X → Y が存在して, (1) H(0,x)=φ0(x) かつ, を満たしていることである。 ここで,H(t,x)を φ0〜φ1のホモトピーと呼ぶ。 |
X=[0,1] であれば,ループどおしのホモトープと同じになります。同じ1次元で考えるならば,例えば,X=S1(円周=1)として,下図のような連続写像がこの定義の基点を保ったままホモトープという
ことになります。(この連続写像ならば,具体的な数式でも表せますが,ここに書くのは止めておきます。)
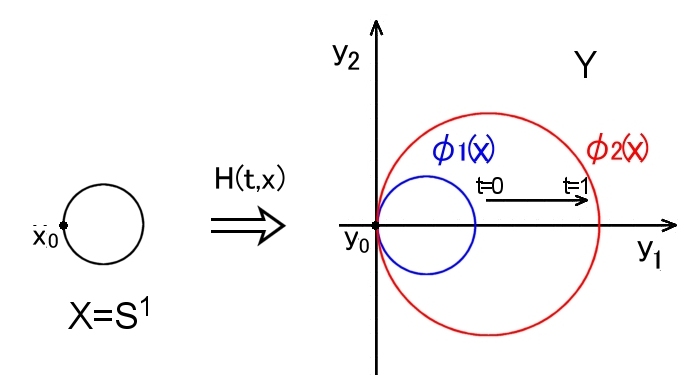
Xが球面であれば,上図の円を球面としてイメージすればよいでしょう。
[5]
|
定義 図形 X と Y がホモトピー同値 弧状連結な図形 X ,Y それぞれの基点を x0 ,y0 とする。 X から Y への連続写像φ:X→Y,および,Y から X への連続写像ψ:Y→X が存在して, ψοφ 〜 idX [ X上の恒等関数 ] φ(x0)=y0 を満たしているとき,φ,ψをホモトピー同値写像といい,φとψはホモトピー的に逆であるという。 また,ホモトピー同値写像が存在するとき,X と Y はホモトピー同値であるといい, X〜Y で表す。 |
「弧状連結な図形 X ,Y 」 の文言は,「位相空間 X,Y 」としてもよい。
例 として最も簡単なものは,
X=R,Y={ 0 } のとき,
φ: X → Y を φ(s)=0 [零写像]
ψ: Y → X を ψ(0)=0
とすると,
ψοφ: X→X ψ(φ(s))=0 零写像 ・・・・ [*]
φοψ: Y→Y φ(ψ(0))=0 恒等写像 idY
となりますが,零写像 [*] が恒等写像 idX とホモトープであることは,
H(s,t)=ts
とすれば,
H(0,s)=0・s=0=ψ(φ(s))
H(1,s)=1・s=s=idX
すなわち,ψ(φ(s)) と idX とはホモトピー同値です。以上,ホモトープの条件(1)が示されました。
条件(2)は φ(0)=ψ(0)=0 である。 ことから直ちに分かります。
結論として,R と { 0 } はホモトピー同値である,ということができます。
しかし,R と { 0 } は位相同型ではありません。ホモトピー同値は位相同型を緩くした概念で,一般的に,
位相同型 ⇒ ホモトピー同値 〇
ホモトピー同値 ⇒ 位相同型 ×
です。
[6] ホモトピー同値の有用性は,
|
(1) X と Y の基本群は同型。 |
ということが成り立つことです。また,位相同型ならばホモトピー同値なので,基本群は位相普遍性のある性質のいうこともできます。
ホモロジー群については次ページで説明します。
[1] 基本群の具体的な計算に必要な初等的な定理を紹介し,トーラスT2の基本群を実際に求めてみましょう。
|
定義 レトラクション 位相空間 X からその部分空間 S (≠φ) への上への連続写像 r の Sへの制限が S上の恒等写像であるとき,r をレトラクション, S を X のレトラクトという。 すなわち, i : S→X (包含写像) を満足する r,S のこと。 (要するにX を S へ連続的に収縮できるような変形ということ) |
基本的なレトラクション,レトラクトを以下挙げておく。
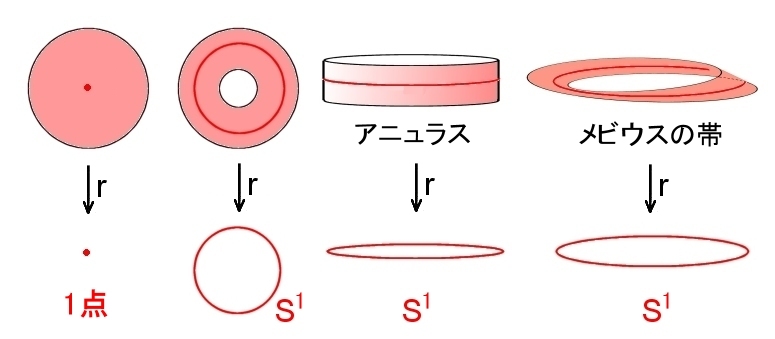
1点にレトラクションできる図形は可縮であるといいます。可縮な位相空間は単連結ですが,その逆は成り立ちません。球面は単連結ですが可縮ではありません。
可縮空間 ⇒ 単連結空間 〇
単連結空間 ⇒ 可縮空間 ×
[2] トーラスから IntΔ2 を取り除いた「穴あきトーラスT’」の部分集合 S (下図に示す) はレトラクトである。
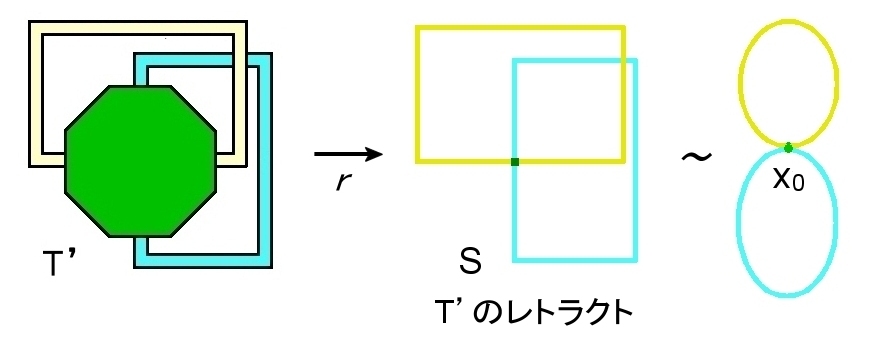
T’のレトラクトは,2つのループが1点で繋がって図形です。
[3]
|
定理3.1 φ: X → Y がホモトピー同値写像ならば,φから誘導される準同型写像, φ*:π1(X,x0) → π1(Y,x0) は同型写像である。 |
言い換えると,
「位相空間 X と Y がホモトピー同値であれば,X と Y の基本群は同型である。」
ということです。
この定理を利用すれば,π1(X,x0) を直接計算する代わりに π1(Y,x0) を計算しても良いことが分かります。
[4] さらに上の定理と次の命題を組み合わせることで,より単純な図形(位相空間)を代用して基本群の計算を行いうことができます。
|
命題 位相空間 X の部分空間 S が X のレトラクトであれば, (1) S と X はホモトピー同値である。 (2) S と X の基本群は同型である。 |
(1)はレトラクションの定義から明らかであり,(1)から(2)は,すぐ上の定理3.1から直ちに分かります。
[5]
|
ファン・カンペンの定理 (1) 位相空間 X,Y について, π1(X∩Y,x0)=e ⇒ π1(X∪Y,x0)=π1(X,x0)*π1(Y,x0) * は自由積 ⇒ [#] |
ファン・カンペンの定理はもう少し一般的に述べることができますが,ここでは基本群の計算に直接利用できる形で紹介しておきます。
2つの円周が1点で接している下図 (〜T’のレトラクト) の場合はほぼ自明でしょう。
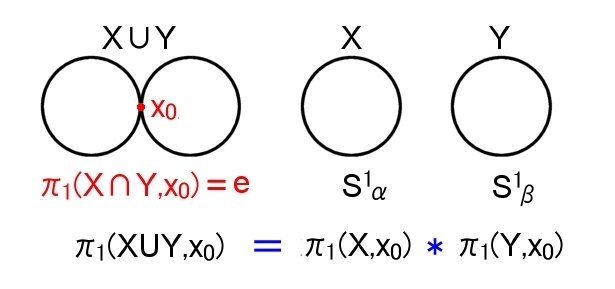
この図形の基本群をファン・カンペンの定理(1)に従って計算すると,
π1(X∪Y,x0)=π1(S1α∪S1β,x0)
=π1(S1α,x0)*π1(S1β,x0)
↓ 円の基本群 ⇒ [#]
=F(α)*F(β)
=F(α,β)
これが ”穴あきトーラス” の基本群 π1(T’,x0) です。
[6]
穴あき多様体の境界Σ1とΔ2の境界∂Δ2とを張り合わせてできる多様体の張り合わせ前後の基本群の関係を示しているのが次の定理です。
|
ファン・カンペンの定理 (2) 連結な多様体 X’と2次元円板 Δ2 とを X’の境界Σ1と∂Δ2とを合わせて貼り合わせてできる多様体を X (=X’∪Δ2) とする。このとき,Σ1上の任意の点を x0とすれば, π1(X,x0)=π1(X’∪Δ2,x0) が成り立つ。 ここで,[h] はループΣ1の属する π1(X’,x0) のホモトピー類であり,([h]) は [h] によって生成される π1(X’,x0) の正規部分群である。 |
要点は,
X’の境界Σ1を1周することに相当するX’の1点x0を基点とするX’のループに同値なすべてのループは,多様体 X’の境界Σ1に円板を張り合わせて塞いでできる多様体 X (=X’∪Δ2) の基本群 π1(X,x0) では [e] に属している。(X上ではΣ1は1点に可縮なので)
ということです。
[7]
例1
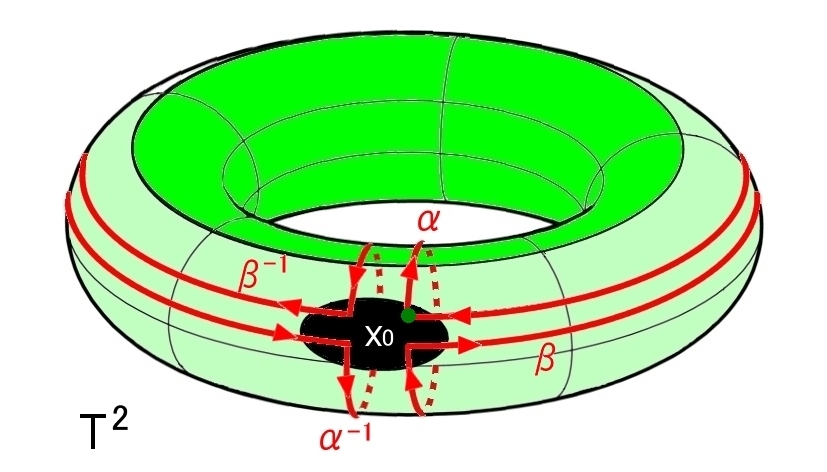
この定理(2)を利用して,T’の基本群からトーラスT2 の基本群を計算する方法を与えておきます。
X’=T’ 穴あきトーラス面
X =T2 トーラス面
として,ファン・カンペンの定理(2)を適用します。
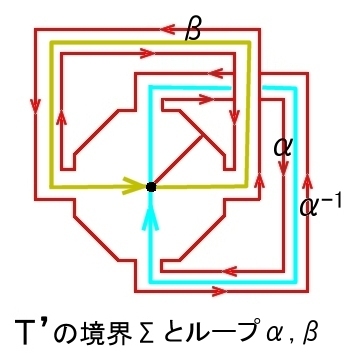 |
 |
|
| T’のΣ1〜αβα-1β-1 | T’の境界αβα-1β-1 (赤い曲線) のトーラスT2上での形。 どこにも引っ掛かることなく1点に収縮させることができる。 |
トーラスは,穴あきトーラスT’の穴(境界Σ1) をΔ2の境界∂Δ2と張り合わせて塞いだ閉多様体なので,ファン・カンペンの定理を利用できます。
T’の基本群 π1(T’,x0) はすでに求めたように自由群 F(α,β) です。
T’の境界Σ1は,上図(左)の赤い閉曲線(ループ)を辿って,αβα-1β-1 ∈ π1(T’,x0) であることが分かります。
よって,ファン・カンペンの定理(2)における”正規部分群”とは,
([h])=([αβα-1β-1])={ x-1αβα-1β-1 x|x∈π1(T’,x0) }
であり,トーラスの基本群は,
π1(T2,x0)=π1(T’∪Δ2,x0)
=π1(T’,x0)/([h])
〜F(α,β)/([αβα-1β-1])
〜<α,β|αβα-1β-1=e> [トーラスの基本群]
と計算できます。
さらに,関係子αβα-1β-1=e はαβ=βα (αとβは可換)と変形すれば,上式は自由積 F(α)*F(β) の可換化 [#] とみなすことができるので,
π1(T2,x0)=F(α)F(β)=Z
Z
トーラスの基本群は階数2の自由アーベル群 Z![]() Z と同型であることが分かります。
Z と同型であることが分かります。
[8]
例2 射影平面の基本群
トーラスの場合と同様に,
(1) 穴あき射影平面 P’のレトラクトの基本群π1(P’,x0) =F(α)を求める。
(2) 穴あき射影平面 P’の境界のループΣ1の属する π1(P’,x0) のホモトピー類[α2]を求める。
(3) ファン・カンペンの定理(2)における”正規部分群”とは,
([h])=([α2])={ x-1α2x|x∈π1(P’,x0) }
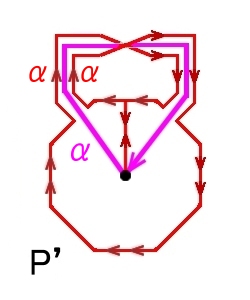
(4) 射影平面の基本群は,
π1(P2,x0)=π1(P’∪Δ2,x0)
=π1(P’,x0)/([h])
〜F(α)/([α2])
〜<α|α2=e> [射影平面の基本群]
〜 Z2
と計算できます。
[9] ここまで説明すれば,2次元閉多様体の標準形の基本群は結果だけ書いておいても問題ないでしょう。
|
定理 閉曲面(2次元閉多様体)の基本群 ・ 向き付け可能な種数 g (≧1) の閉曲面の基本群π1(gT2,x0) 〜 <α1,β1,・・・,αg,βg|α1β1α1-1β1-1 ・・・ αgβgαg-1βg-1=e> 向き付け可能な種数 g=0 である閉曲面はS2と同相で,その基本群は,π1(S2,x0) 〜 { e }・ 向き付け不可能な種数 h (≧1)の閉曲面の基本群 π1(hP2,x0) 〜 <α1,・・・,αh|α12 ・・・ αh2=e> |
(注意) g=1のときは,αg,βgは可換なので,π1(T2,x0) =Z![]() Z であることはすでに述べましたが,g≧2では,π1(gT2,x0) ≠Z
Z であることはすでに述べましたが,g≧2では,π1(gT2,x0) ≠Z![]() Z
Z![]() Z
Z![]() …
…![]() Z
Z![]() Z (2g個のZ) とはなりません。そのように表せるためにはαj,βk (g=1,2,…,g )がすべて互いに交換可能である必要があります。
Z (2g個のZ) とはなりません。そのように表せるためにはαj,βk (g=1,2,…,g )がすべて互いに交換可能である必要があります。
ループを繋ぐ演算で群になることの確認
単位元の存在
[e] [φ]=[eφ]=[φ] を満たす [e] の存在を示す。
連続写像を,
| H(t,s)= | x0 (s≦(1-t)/2) | |
| φ((2s-1+t)/(1+t)) (s≧(1-t)/2) |
とおくと, ホモトープの条件 (1) について,
| H(0,s)= | x0 (s≦1/2) | |
| φ(2s-1) (s≧1/2) |
=e・φ(s) (0≦s≦1)
| H(1,s)= | x0 (s≦0) | |
| φ(s) (s≧0) |
=φ(s) (0≦s≦1)
ホモトープの条件 (2)について,
| H(t,0)= | x0 (0≦(1-t)/2) | |
| φ((-1+t)/(1+t)) (0≧(1-t)/2 |
| = | x0 (t≦1) | |
| φ((-1+t)/(1+t)) (t≧1) |
=x0 (0≦t≦1)
| H(t,1)= | x0 (1≦(1-t)/2) | |
| φ((1+t)/(1+t)) (1≧(1-t)/2) |
| = | x0 (t≦-1) | |
| φ(1)=x0 (t≧−1) |
= x0 (0≦t≦1)
よって,ループ e・φとφとはホモトープである。すなわち,
[e] [φ]=[φ]
を [e] は満足する。
逆元の存在
| H(t,s)= | φ(2st) (s≦1/2) | |
| φ-1(1+2t(s-1)) (s≧1/2) |
とおくとよい。
ホモトープの条件 (1) は
H(0,s)= φ(0) (s≦1/2) φ-1(1) (s≧1/2)
= e(s) (0≦s≦1)
H(1,s)= φ(2s) (s≦1/2) φ-1(1+2(s-1)) (s≧1/2)
=φ・φ-1(s) (0≦s≦1)
ホモトープの条件 (2) は
H(t,0)=φ(0)
=x0 (0≦t≦1)
H(t,1)=φ-1(1)
=x0 (0≦t≦1)
よって,φ・φ-1と e とはホモトープである。
弧状連結な位相空間をX,弧状連結なその部分空間をSとするとき,連続写像 H : [0,1]×X → X が
(1) H(0,x)=x
H(1,x)∈S ( ∀x∈X )
(2) x∈Sについて,H(t,x)=x ( ∀t∈[0,1] )
であるときは,変位レトラクションという。
|
まず,用語の補足から, 弧状連結な位相空間 X, X~ と連続写像 p : X~ → X が次の条件を満たすとき、X~,または (X~, p ) を X の被覆空間という。 (1) p-1(U) = Uλ∈ΛU~λ は互いに交わらないU~の開集合の和集合 (2) 制限 p|U~λ : U~λ→U は位相同型写像 ここで、X を底空間、p を被覆写像、p-1(x) を x 上のファイバーという。
ループφ:[0.1] → S1の回転数n とは,φ~(0)=0,かつ,φ~(1)=2nπとするときの n として定義。 n はφのホモトピー類と1対1に対応する。 n : π1(S1,x0) → Z は全単射準同型写像である。 ことをもって,π1(S1,x0) 〜 Z の証明とする。 |
連結な位相空間の部分集合A が開集合,かつ,閉集合であれば,A=φまたは A=X
である。
--------------------------