| Appendix b4 直積と半直積 | ||
| f-denshi.com 更新日: 21/09/13 | ||
| [目次へ] | ||
[1] 群AとBとの直積集合[#]として,
(aj,bj), ただし,aj ∈A, bj ∈B ,演算は*及び*とする
を考えます。この元の間に次のような群の演算 ” * ”
(a1,b1)*(a2,b2) = (a1*a2,b1*b2)
を定義できます。
* は群の演算として意味をもてば何でも構いませんが,加法の場合では,
(a1,b1)+(a2,b2) = (a1+a2,b1+b2)
と書くことにします。
具体例して,2つのZ2の直積は群となりますが,その群表を下に示します。
+ ([0]2,[0]2) ([1]2,[0]2) ([0]2,[1]2) ([1]2,[1]2) ([0]2,[0]2) ([0]2,[0]2) ([1]2,[0]2) ([0]2,[1]2) ([1]2,[1]2) ([1]2,[0]2) ([1]2,[0]2) ([0]2,[0]2) ([1]2,[1]2) ([0]2,[1]2) ([0]2,[1]2) ([0]2,[1]2) ([1]2,[1]2) ([0]2,[0]2) ([1]2,[0]2) ([1]2,[1]2) ([1]2,[1]2) ([0]2,[1]2) ([1]2,[0]2) ([0]2,[0]2)
このような加群は直和加群といい,Z2![]() Z2 のように書きます。
Z2 のように書きます。
[2] 今度は乗法群の例を考えてみます。直積の演算としては集合 Z2={1,-1} は通常の「掛け算」で群となります。乗積表は,
* 1 -1 1 1 -1 -1 -1 1
となります。ここで,Z2とZ2の直積の元の間に次のような積 ” * ”
(a1,b1)*(a2,b2) = (a1a2,b1b2)
を定義すると,この直積集合は群となり,下のような乗積表を作ることができます。
* (+1,+1) (-1,+1) (+1,-1) (-1,-1) (+1,+1) (+1,+1) (-1,+1) (+1,-1) (-1,-1) (-1,+1) (-1,+1) (+1,+1) (-1,-1) (+1,-1) (+1,-1) (+1,-1) (-1,-1) (+1,+1) (-1,+1) (-1,-1) (-1,-1) (+1,-1) (-1,+1) (+1,+1)
この群を Z2 と Z2 の直積(群)といい,Z2×Z2 と書きます。
この2つの群表からこの2つの群は実質的に同じで,各元について,次のような対応が付けられます。
(+1,+1) ⇔ ([0]2,[0]2)
(-1,+1) ⇔ ([1]2,[0]2)
(+1,-1) ⇔ ([0]2,[1]2)
(-1,-1) ⇔ ([1]2,[1]2)
すなわち,Z2![]() Z2 と Z2×Z2 は同型です。
Z2 と Z2×Z2 は同型です。
この場合は,2つの直積の同型ですが,同じ型どおしの直積に限らず,同型な群を他に見出すこともできます。次にその例を見てみます。
[2] 2つの群が同型であるならば,少なくともその群の位数は等しくなければなりませんので,|Z2× Z2|=4 であることからクラインの4元群とよばれるこの群と同型な群の位数も4でなければなりません。
そのような群として, 2面体群 D2 [#]や正四面体群の正規部分群 H [#]を挙げることができます。その群表は下のとおりです。
* 1 c σ cσ 1 1 c σ cσ c c 1 cσ σ σ σ cσ 1 c cσ cσ σ c 1
* e hx hy hz e e hx hy hz hx hx e hz hy hy hy hz e hx hz hz hy hx e 2面体群 D2 A4の正規部分群 H の乗積表 [#]
これらの群表と比較してみると,実質的に同じ表であることがわかります。つまり,対応(=同型写像),
(+1,+1) ⇔ ([0]2,[0]2) ⇔ 1 ⇔ e
(-1,+1) ⇔ ([1]2,[0]2) ⇔ c ⇔ hx
(+1,-1) ⇔ ([0]2,[1]2) ⇔ σ ⇔ hy
(-1,-1) ⇔ ([1]2,[1]2) ⇔ cσ ⇔ hz
を考えれば,この4つの群が同型であるとわかります。
Z2Z2 = Z2×Z2 = D2 = H (正四面体の正規部分群)
このようにある群が直積群と同型であることはしばしば起こります。2面体群D2については⇒[#]
[3] 以上のことを一般化してみましょう。
|
定義 G に部分群 H1,H2 が存在して,h1∈H1,h2∈H2 とする。 (1) H1と H2 の元は可換である。h1h2=h2h1 このとき,g ∈G を H1,H2 の直積 H1×H2 の元 (h1,h2) に1対1に同型対応させることができる。 |
(1),(2) を直積 (h1,h2) の定義とすることができます。
[4] それでは,どのような群が直積で表す(=(直積)分解されるという)ことが可能なのでしょうか。その答えを与えるのが次の定理です。
| 定理1 群 G とその正規部分群,H1,H2 について, (3) G = H1H2 , H1∩H2 = {e} の関係を満たすならば, (4) G = H1×H2 ⇔ 定義 (1),(2) を満たす と表すことができる。逆も成り立つ。 |
証明
⇒ (必要性)
(1) H1,H2 を正規部分群 [#] とすれば,
h1-1(h2-1 h1h2) = h1-1h2-1 h1h2 = (h1-1h2-1 h1)h2 H1の元 H2の元
より,h1-1h2-1 h1h2 は H1∩H2 の元であるが,H1∩H2 = {e} なので,
h1-1h2-1 h1h2 = e ⇔ h1h2=h2h1
である。これで定義 (1) は示せた。
(2) 定義 (2) の一意性については,
g=h1h2=h'1h'2 ( h1,h'1∈H1, h2,h'2∈H2 )
とおいて,この式に左から h1-1,右から h'2-1をかけると,
h2h'2-1=h1-1h'1
が成り立つ。
左辺∈H2,右辺∈H1より,この積で表されている元は H2∩H1 の元である。
(3) ところが,H1∩H2 = {e} であるから,
h2h'2-1=e ⇔ h2=h'2
h1-1h'1=e ⇔ h1=h'1
でなければならない。
よって,G の元は一意的に g=h1h2 (h1∈H1,h2∈H2) と表される。
逆 (十分性)
(4) H1とH2 の元が可換で,G の任意の元が g=h1h2=h2h1 と一意的に表せるとすれば,g-1=h2-1h1-1=h1-1h2-1 である。
(5) すると,
g-1H1g=h2-1h1-1H1h1h2
=h2-1H1h2 ← H1と h2は可換
=H1
これは,H1が G の正規部分群であることを示している。
(5) H2が G の正規部分群であることも同様に示すことができる。
(6) 一方,任意の元 h∈H1∩H2 ⊂G と,単位元 e∈H1∩H2 に対して,
h=he=eh
であるが,h の積表現の一意性より,h=e=ee でなければならない。
証明終
[5]
例
D2 に関して確かめてみましょう。 H1={e,c},H2={e,σ}とすれば,
H1H2={ee,eσ,ce,cσ}={e,σ,c,cσ}=G
G = H1H2,H1∩H2 = {e=1}を満足していることが分かります。したがって,直積に分解可能です。
cf.H3={e,cσ} も D2 の正規部分群なので,G=H1H3=H2H3 と表現することもできます。
[1]
| 定義: 半直積 群 G とその正規部分群 H,および,(正規部分ではない)部分群 S について,次のような関係, G = HS,H∩S = {e} であるとき,G は H と S の半直積であるという。 言い換えると, 「G の任意の元 g が一意的に g = hs (h∈H,s∈S) と表される 」 とき,G は H と S の半直積であるという。 |
注意: 群 G を半直積 HS に分ける仕方は一意的とは限りません。
[2] 半直積の例を具体的に見てみましょう。
例1
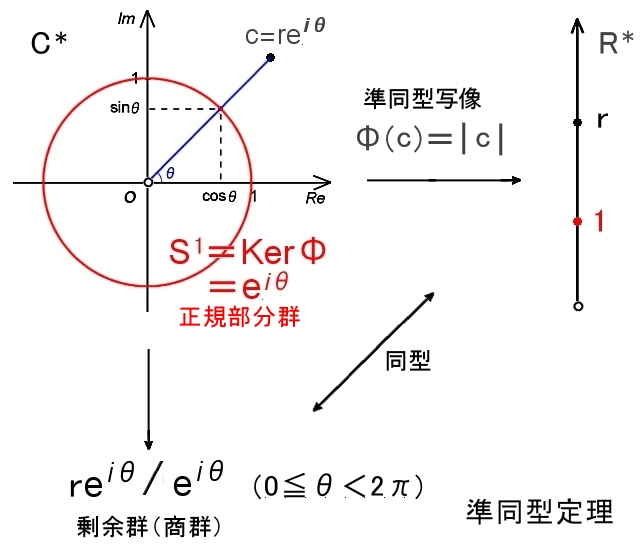
原点の除く複素平面上の点全体からなる乗法群 C*の元(点)を極座標表示で,
c=r・eiθ
と書いてみると,複素平面の部分集合 R+ :正の実数全体の点 r と同じく複素平面の部分集合である S1:単位円上の点 eiθの積として一意的に表されます。
この様子は,
C*=S1R+
と書くことができます。 S1がC*の正規部分群であることを示したいのですが,そのために準同型写像
Φ(c)=|c|
を考えます。これは,ImΦ=R+ であり,その核は
KerΦ=eiθ,(0≦θ<2π) ≡ S1
であることが分かります。
そして準同型定理より,S1はC*の正規部分群であることが分かります。
例2
2面体群 Dn は正規部分群 Zn と部分群 Z2 の半直積である ⇔ Dn=Zn Z2 かつ, Zn ∩ Z2= 1
[3] 半直積群と準同型写像との関係
これは例を見てみましょう。
| 準同型写像 | 核 | 準同形定理 | 半直積 | |
| 乗法群 R* ⇒ R+ | f(x)=|x| | S0 | R*/ S0= R+ | R*=S0 R+ |
| 乗法群 C* ⇒ R+ | f(c)=|c| | S1 | C*/ S1= R+ | C*=S1R+ |
| 加群 R ⇒群 S1 | f(x)=e2πi x | Z | R/Z=S1 | R=ZS1 |
| GL(n,K)⇒K* | f(A)=detA | SL(n,K) | GL(n,K)/SL(n,K)=K* | GL(n,K)=SL(n,K)K* |
| O(n)⇒S0 | f(A)=detA | SO(n) | O(n)/SO(n)=S0 | O(n)=SO(n)S0 |
| U(n)⇒S1 | f(A)=detA | SU(n) | U(n)/SU(n)=S1 |
U(n)=SU(n)S1 |
| A(Rn)⇒GL(n,R) | f(Ax+σ)=A | D(Rn) | A(Rn)/D(Rn)=GL(n,R) | A(Rn)=D(Rn)GL(n,R) |
| E(Rn)⇒O(n,R) | f(Ax+σ)=A | D(Rn) |
E(Rn)/D(Rn)=O(n,R) |
E(Rn)/D(Rn)O(n,R) |
|
R*=R−{0}, |
S0∩R+=1 S1∩R+=1 SO(n)∩Sn0 = 1 SU(n)∩Sn1 = 1 D(Rn)∩GL(n,R)=1 D(Rn)∩O(n,R)=1 |
以上は,群 G の正規部分群 H とその剰余群 S=G/H を考えると,G=HS のように G を H と S の半直積で表される場合です。
つづく,・・・
半直積で表せない:4元数群 Q8
|
⇒ 商群 |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
| (2) R*=S0×R+ ; | f(x) | = | (sgn x,|x|) | , g(σ,x) | =σx | |
| R* | → | S0×R+ | S0×R+ | →R* |
(3) ユニタリ群 U(n) は正規部分群 SU(n) と部分群 Sn1
Sn1 ={ c 0 0 0 | |c|=1,c∈C } 0 1 0 0 0 0 : 0 0 0 0 1
の半直積である。 ⇔ U(n)=SU(n)Sn1, SU(n)∩Sn1 = 1
(4) 直交群 O(n)は正規部分群 SO(n)(回転)と部分群(反転)Sn0:
Sn0 ={ 1 O , -1 O } 1 1 O : O : 1 1
の半直積である。 ⇔ O(n)=SO(n)Sn0, SO(n)∩Sn0 = 1