| 1-1 実射影空間 | ||
| f-denshi.com [目次へ] 最終更新日: 23/05/04 | ||
| サイト検索 | ||
「m+1次元ユークリッド空間の原点 0 を通る直線全体からなる集合{Pm}」 から構成される位相空間を RPm ( 教科書によっては Pm ) と書いて実射影空間といいます。
位相空間とするためには集合{P}に位相を入れないといけませんが,それはユークリッド空間から商位相 [#] として導入します。
{1] 実射影空間の定義です。
| 定義(その1) [実射影空間]
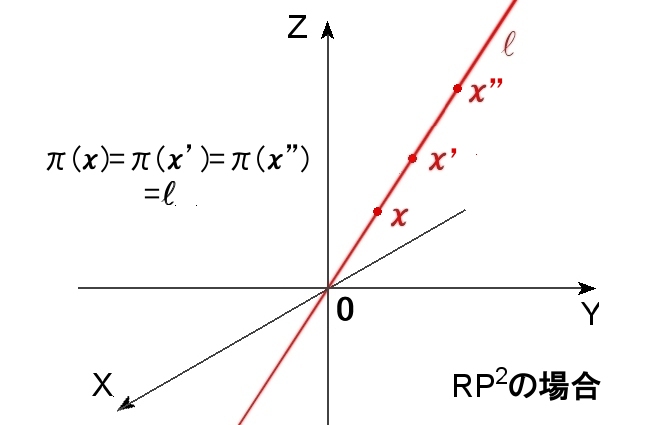
m+1次元ユークリッド空間 Rm+1の原点 0 を除いた Rm+1−{0} から,原点 0 を通る直線l 全体からなる集合{Pm}への上への写像を, π: x → l (原点0 とx を通る直線) と定義し,自然な射影という。ここで,x ∈Rm+1−{0} ,l ∈{Pm}。 さらに,この π によって, Rm+1−{0} の商位相を{Pm}へ導入した位相空間をRPmと書いて実射影空間という。 |
πが{Pm}の全体への上への写像であることは自明でしょう。また,ある一つの直線上にある Rm+1−{0} のすべて点x は,すべてその直線に写されるので,πは無限個の点を1本の直線へ対応させる写像であることも分かります。
[2] 次に定義に現れる商位相について説明していきましょう。位相空間論1 [#] から抜粋すると,
位相空間(X,U X) から単なる集合 Y への写像が存在するとき,Y の部分集合族
U Y={ UY⊂Y|f-1(UY)∈U X }
を考えると,U Y は Y の位相の条件を満たす。このU Y をU X の商位相といい,(Y,U Y )を(X,U X) の商空間という。
( 補足:U X はXの位相でUYより細かい,また,f(UX)=UY とする。)
今考えている実射影空間に当てはめるには,X→Rm+1−{0},Y→{Pm}とすればよいでしょう。ただし,記号が饒舌になるので,ここでは,
UX→ O, UY → V
と書くことにします。つまり,{Pm}に導入される位相 (開集合族) は,
U {Pm}={ V⊂{Pm}|π-1(V) ∈U Rm+1−{0} }
となります。そして,この位相が与えられた{Pm}を RPm と書くことにします。
[3] 具体的なイメージとして,任意の開集合 O∈U Rm+1−{0} で,π(O)=V とするとき,
π-1(V)= U l−{0} l∩O≠φ
を Rm+1−{0} 空間に図示すると, m=2 の場合を下図 (のピンク色の部分) のようになります。
(Vそのものは2次元ユークリッド空間には描けない。)
|
|
| 原点から0から開集合Oを通る直線全体からなる集合をピンク色で示している。 ただし,Oの境界に外接する直線(その一部を破線で示している),および原点は含まない。 この領域は Rm+1−{0} の開集合である。 |
π-1(V)はU Rm+1−{0} における開集合なので,VはRPmの開集合です。
よって,任意の開集合Oに対応して,Vの開集合がπによって定まり,商位相がRPmに入ることになります。
[4] さらに,RPmが位相多様体であるためには,
1.RPmはハウスドルフ空間である。
2.RPmは座標近傍系で被覆できる。
を示す必要があります。
1.を示すには任意の異なる2本のl1,l2 に対して,ある開近傍 V1,V2が存在して,V1∩V2≠φとなっていればよい。
(1) それには,R3−{0 } における異なる2本の直線 l1,l2 上の 0 でない点x1,x2はx1≠x2であり,それぞれの点を中心とする十分小さな開円板 O1,O2を考えると,ユークリッド空間に入っている自然な位相の性質から O1∩O2=φとすることができる。
(2) そこで,π(O1)=V1,π(O2)=V2を考えると,これらはl1,l2 の開近傍であり,V1∩V2=φとなっている。
(もし,V1∩V2≠φだとすれば,V1∩V2を開近傍とする原点を通る直線が存在して,かつ,その直線はO1とO2の両方を通ることになるが,O1とO2の選び方からそのような直線は存在しない。矛盾。)
以上より,1.ハウスドルフ空間であることが分かりました。
[5] 次に2.ですが,具体的に局所座標近傍を示し,それらの和集合がRPmの座標近傍系(アトラス)となっていることを確認すればよいでしょう。
それは,Rm+1の各座標軸の1と垂直に交わる m+1個のm次元ユークリッド空間 を考えることで実現できます。
次元を一般化するのは容易なので,R3−{0 },RP2の場合で具体的に局所座標系を示してみましょう。
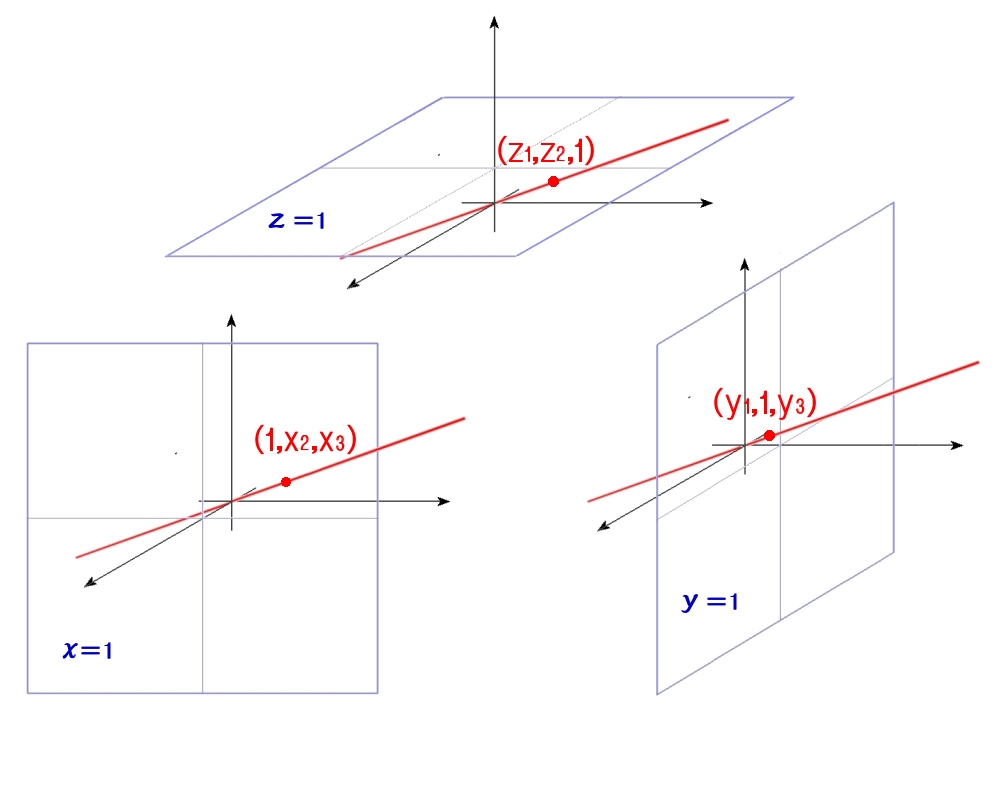
RP2の点に対応するR3上の直線l は,X軸と1で垂直に交わる2次元ユークリッド空間 (平面 X=1) と交わる場合,1点 (1,X2,X3) でだけ交わります。l からこの平面との交点への同相写像をχ1とします。
他のY,Z軸に対しても同様な平面との交点を考えて,その点を (Y1,1,Y3),(Z1,Z2,1) ,対応する同相写像をχ2,χ3とします。
次にそれらの平面を2次元ユークリッド空間R2と同一視して,これらの点をR2へ写す写像ψkを次のように定義します。
ψ1 : (1,X2,X3) → (X2,X3)
ψ2 : (Y1,1,Y3) → (Y1,Y3)
ψ3 : (Z1,Z2,1) → (X2,X3)
これらの写像ψkは同相写像であり,l と各平面との交点への写像χkも同相写像なので,その合成写像
φk=ψkοχk ; k=1,2,3
は,RP2の点からR2への同相写像であることが分かります。つまり,これら3つともRP2の局所座標系 [#] となっています。また,明らかにこれらは C∞級写像です。
そして,RP2の「点」に対応するであるR3の原点を通る直線l は,3つの平面のいずれかと必ず交わるので,RP2の任意の 「点」 は3つのいずれかの局所座標 (Vk,φk) を用いて表すことができます。したがって,RP2=V1UV2UV3の座標近傍系は,Ok=R2,π(Ok)=Vk として,
S = { (V1,φ1),(V2,φ2),(V3,φ3) }
とすればよいことが分かりました。
これで,RP2が級の2次元多様体であることが証明されました。
[6] 一般のRPmについても考え方は同じなので,概略だけを以下に示しておきます。
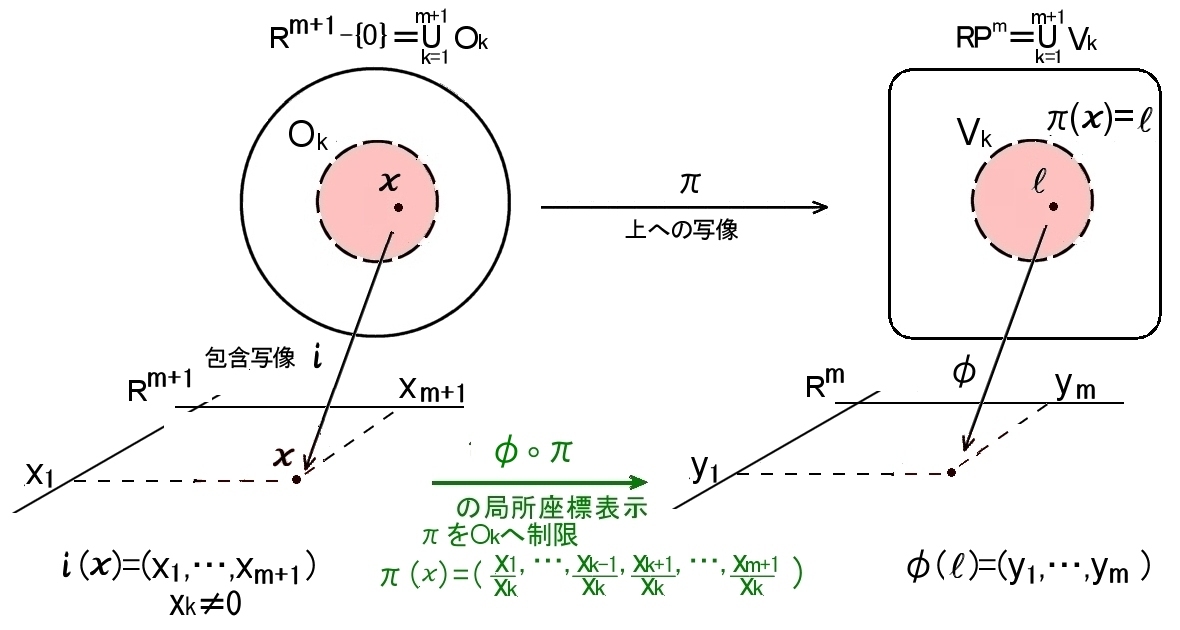
(1) まず,開集合,
Ok={x =(x1,x2,…,xk,…,xm+1)|xk≠0)}
π(Ok)=Vk
を定めると,
Rm+1−{0 } = m+1 Ok U k=1
RPm = m+1 Vk U k=1
と被覆されることを確認する。
(2) 次に,x =(x1,…,xm+1)∈Rm+1−{0} を与えることで定まる直線が,
lx,∈Vk ( k=1,2,…,m+1 )
であるとき, Rm+1上のk番目の座標を除いたm次元ユークリッド空間と,
φk(π(x))= x1 , x2 ,…, xk-1 , xk+1 ,…, xm+1 xk xk xk xk xk
の1点でだけ交わること, つまり,φkは同相写像であることを示す
。
(3) すると,x は成分 xk (k=1,2,…,m+1) のいずれかは 0 ではないので,RPmの座標近傍系がm+1
個の座標近傍,
S = { (V1,φ1),(V2,φ2),・・・,(Vm+1,φm+1) }
で与えられることが分かります。
以上の様子は上の図を参考にしてください。
[1] m=2 の場合の実射影空間を実射影平面といいます。平面とは言っても3次元ユークリッド空間の中で眺めることは不可能 (=3次元ユークリッド空間に埋め込むことはできない)ので,その具体的な図形的なイメージを掴むのは簡単ではありません。その説明の適した別の射影空間の定義を与えておきましょう。
| 定義 (その2)
m+1次元ユークリッド空間 Rm+1の単位球面である多様体 Sm 上の点 x と原点に関して点対称な点 -x (x の対蹠点) を同一視してできる多様体をRPmと書いて実射影空間という。 |
このページの冒頭に示した定義において, Rm+1−{0} をその部分空間 Sm に制限したと考えることもできます。
下図には m=2 の場合の様子を示します。
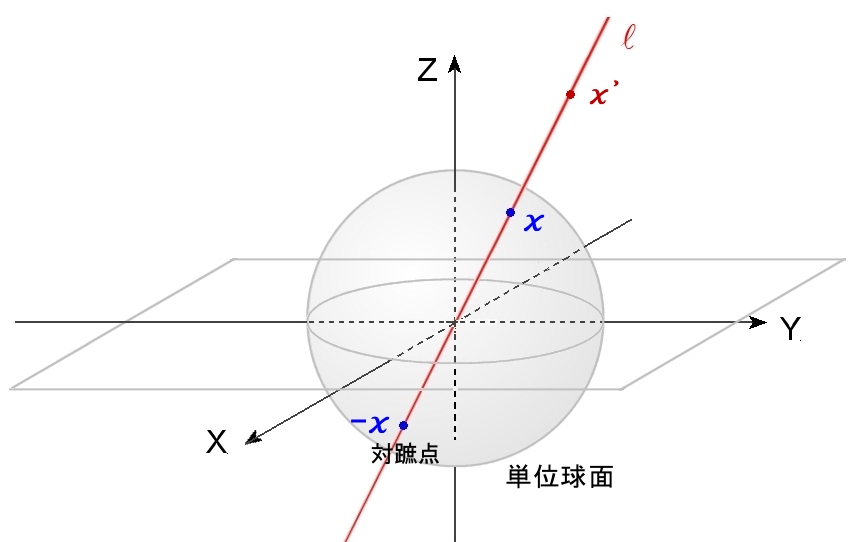
RP2上の1点は1本の直線に対応するのに対して,S2上では2点が一本の直線に対応しています。S2が多様体であることはすでに示してあります ⇒[#]。すると,直感的にも S2上の2点 x と -x を同一視すると,それはRP2と同一の多様体になるであろうと納得できます。
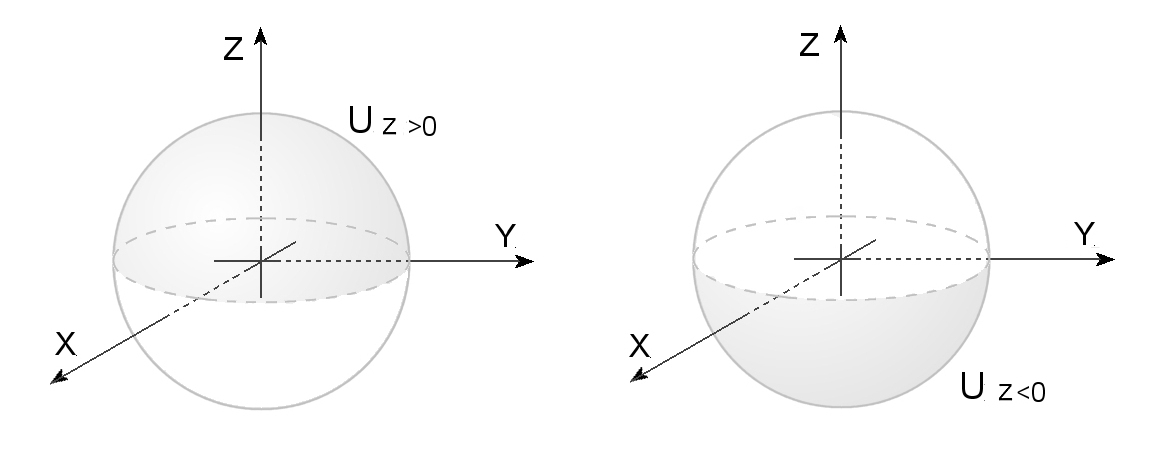
実際,Π: S2 → RP2 は上への 2:1 のC∞級同相写像写像となっています。つまり,
Π(Ux>0)=Π(Ux<0)=V1
Π(Uy>0)=Π(Uy<0)=V2
Π(Uz>0)=Π(Uz<0)=V3
そして,Πの局所座標表示を求めてやれば,それがC∞級同相写像であることも容易に確かめられます。
また,それを一般次元に拡張することも容易です。
[2] 射影平面を図形として,どのようにイメージするかという話しに戻りましょう。球面上のx に対して, -x を対蹠点といいますが,RP2 を考える上では,S2上の対蹠点を一方を無視しても構わないでしょう。北半球を考慮すれば,対応する南半球は棄て去っても良いということです。(=南半球の凹凸を「逆にしてから北半球の対応する対蹠点どおしを重ね合わせる)
このとき,赤道上の点は残しておくようにします。これを実射影平面とみなすには,さらに赤道上の各点を,180°反対側の対蹠点と同一視する必要がありますが,それを実行するためには技巧を必要とします。
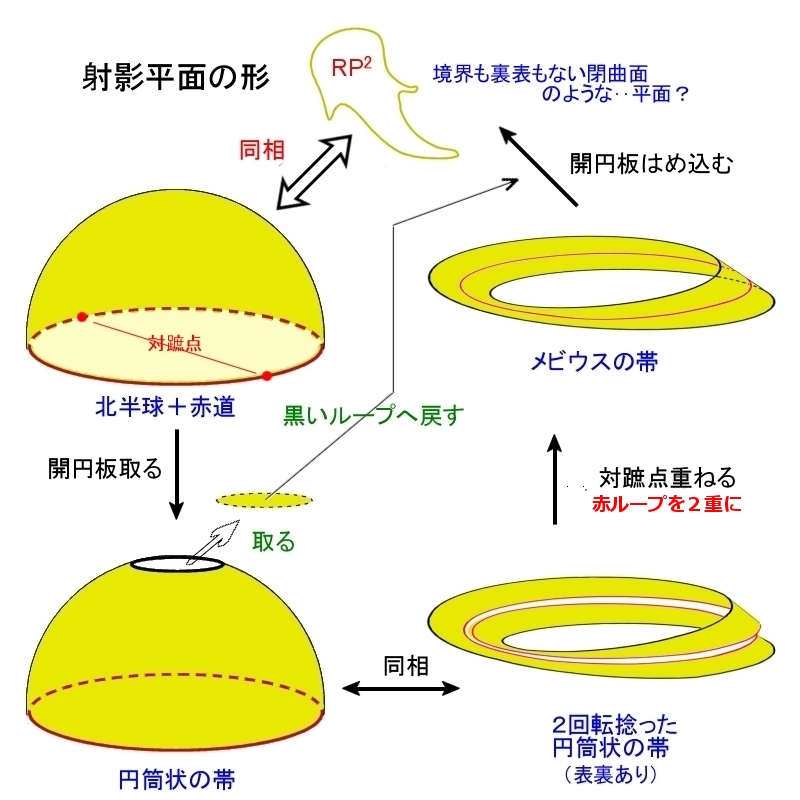
以下,上図を参考にしながら読んでください。先ず,
(1) 北半球の一部から開円板を取り除く
すると,残った部分は円筒(の側面)と同相な図形となります。次に,
(2) 円筒に切れ目を入れて2回転捻って同じ部分どおし再び張り合わせる。
その結果得られる図形は元の円筒と同相な表裏のある閉じた帯状の図形です。
どちらも右手に赤色=赤道の境界,左手に黒色=開円板の穴の境界を見ながら進んでいけば,元の点に戻ってくることができますね。
(3) 赤い境界上の対蹠点を重ねるように帯の境界を張り合わせる。
この操作はメビウスの帯の中央に沿って鋏を一周入れて切り開く操作のちょうど逆の操作です。
したがって,その結果できる図形はメビウスの帯です。これは裏表のない最も著名な図形です。
(4) 黒いループに沿って,開円板を元々の位置に張り合わせる。
この最後の操作は3次元空間ではイメージできませんが,黒い境界線をすぐ左に眺めながらすっと同じ方向に進んでいけば元のところに戻って来られるわけですから,開円板の境界をそれに合わせるように貼っていけばいいわけです。
その結果出来上がる図形はRP2と同相な図形ですが,境界がない,裏表がない,3次元では描くことのできない有界な図形となっています。
また,定義(その2)から実射影平面内の 「直線は球面上の大円として定義できる」 であろうことが分かります。そして2つの大円は球面上で2点で交わりますが,その点は互いの対蹠点となっており,実射影平面上では同一の点です。つまり,「実射影辺面上の異なる2本の直線は必ず1点で交わる」ことが分かります。
[3] RP2 と R3との関係は,
RP2をR3にはめ込むことができる。
というのが正解なのですが,それは外部サイト,
「 The Boy surface 」 Jos Leys
を参考にしてください。
[4] 4次元ユークリッド空間に対しては,
RP2はR4に埋め込めことができる。
ことも分かっています。具体的には,
S2={ x =(x,y,z)∈R3|x2+y2+z2=1 }
として,S2 から R4への写像,
f: (x,y,z) → (yz,zx,xy,x2+2y2+3z2)
を考えると,
f(x )=f(-x )
であるから,単位球面を用いた RP2 の定義を利用すれば,これは多様体 RP2 から R4への同相写像とすることができるのです。