| 6-1 余接ベクトル空間 | ||
| f-denshi.com [目次へ] 最終更新日:22/04/10 校正中 | ||
| サイト検索 | ||
[1]
| 定義
接ベクトル空間 Tp(M) の双対空間を Tp*(M) と書いて,多様体 M の点 p における余接ベクトル空間という。 |
Tp(M) はベクトル空間でした[#]。したがって,対応する双対空間を考えることができ,それを Tp*(M) と表すこととします。
ωp∈Tp*(M) とすれば,それは線形関数に相当するもののはずです。それをきちんと書いておくと,
| 定義
接ベクトル空間 Tp(M) から R への関数 ωp: Tp(M) → R が任意の Xp,Yp∈Tp(M) と任意の実数 a,b に対して, ωp(aXp+bYp)=aωp(Xp)+bωp(Yp) が成り立つとき,1次形式という。(=多様体上の線形関数に相当) |
となります。もう一つ,
| 定義 1次微分形式
Cr 級多様体 M の各点 p ∈M に対して,ωp∈Tp*(M) が一つずつ対応しているとき,その対応, をM上の1次微分形式といい,ω={ωp}p∈M と書く。 |
これは接ベクトル場 X に双対な場とみなせるので,余接ベクトル場と呼ぶこともできます。
(ここではωp は微分(df)pに相当しますが,次ページで見るように2次以上の形式に対しても同じ記号ωpを使います。)
[2] ω={(ω)p}p∈M ,η={(η)p}p∈M を多様体M上の1次微分形式とし,また,M から R への任意の関数を f とするとき,和,倍を,
和 : ω+η={ωp+ηp}p∈M
倍 : fω = { f(p)ωp }p∈M
と定義すると,和・倍の演算後も1次微分形式となることは,ωp,ηpが ”(双対空間の元) べクトル” として振る舞うことから容易に分かります。
さらに,M上のベクトル場 X={Xp}p∈M と1次微分形式 ω={ωp } が与えられているとき,各 p点において,接ベクトル Xp と1次形式 ωpから,
ωp : Xp → R ; (Tp(M) → R )
という実数への対応を考えることができますが,これを
ωp(Xp) ∈R
と書き, M上の点 p ∈M からこの実数値の関数として,
ω(X) : p → ωp(Xp)
を定義することもできます。
[3] このとき,次の公式が成り立ちます。
公式 (1) (fω+gη)(X)=f (ω(X))+g (η(X))
(2) ω(fX+gY)=f(ω(X))+g(ω(Y))
ここで,f,g はM上の任意の関数です。ベクトル・線形関数の性質を多様体上の場に拡張したものです。
[1] 1次形式の場合は,
記号的には, ωp ⇔ (df)p と対応する
すなわち,多様体 M から1次元多様体 R (座標を y と表す) への写像(関数),
f : M → R
に関する微分 [#],
(df)p : Tp(M) → Tf(p)(R)
を考えると,これは線形写像です。Tf(p)(R)の元は,Rを1次元多様体とみて,
a ∂ f(p) ∂y
| つまり,実数 a と多様体R の基底 | ∂ | f(p) | で表されます。 | |||
| ∂y |
これを実数 a と同一視すれば,(df)p は,
(df)p : Tp(M) → R
という1次形式であり,(df)p は余接ベクトル空間 Tp*(M) の元です。
また,各点 p∈M から (df)p∈Tp*(M) への対応 {(df)p}p∈M は M上の1次微分形式であって,添え字p を取り除いて df と書くこととします。
[3] まとめです。
| 定義 Cr級多様体 M から Rへの Cr級関数 f が M上の各点で与えられているとき, df : p → (df)p (∀p∈M )を M上の1次微分形式 (または,全微分)といい, df = { (df)p }p∈M (線形関数全体に相当する概念)と書く。ただし,(df)p ∈Tp*(M) で, (df)p : Tp(M) → Tf(p)(R)=R |
続きの説明も下図を参考にして下さい。
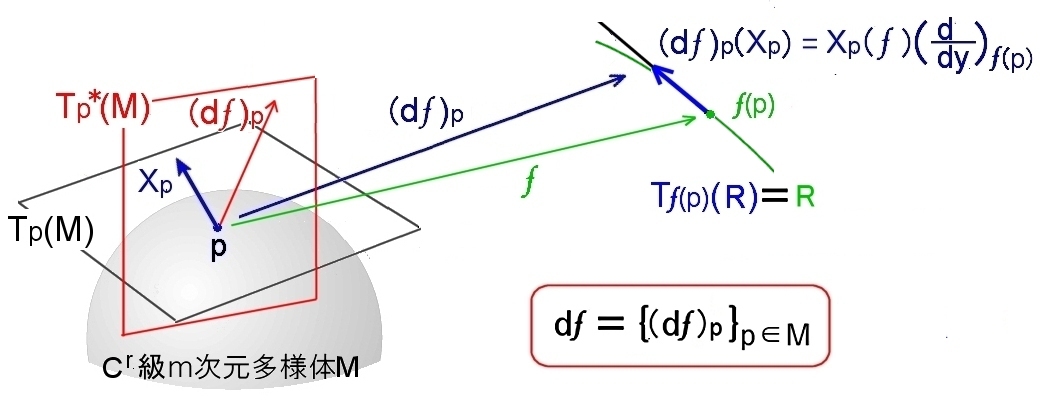
(数直線(緑)は敢えてカーブさせて描いています。)
[3]
公式1
|
この公式の意味は,
左辺=1次形式(線形写像)(df)p をベクトル Xpに作用させる,
右辺=方向微分としての Xp を関数 f に作用させる
ことで,1次元多様体Rへの実数値を対応させることが等価であることを示しています。これは多様体の微分のところで述べた公式3 の値域が R の場合に相当します。
| 命題
Cr級 m次元多様体 M の座標近傍を (U,x1,x2,…,xm) とするとき,各点 p∈U における接ベクトルの基底,
に対応する双対基底 (余接空間の基底) は, (dx1)p,(dx2)p,…,(dxm)p ∈Tp*(M) である。すなわち,
が成り立つ。 |
証明
| これは,Xp= | ∂ | p | の場合を考えれば, | ||||
| ∂xk |
(dxj)p ∂ p = ∂ p (xj) ∂xk ∂xk
= ∂xj p ∂xk
= 1 (j=k) 0 (j≠k)
と示すことができます。
( 双対基底 : e j(ek )=δj k ⇒ [#] をみよ。)
[5] 座標近傍 ( U,x1,x2,…,xm ) が与えられているとき,ωp∈Tp*(M)
ωp=f1(p)(dx1)p+f2(p)(dx2)p+…+fm(p)(dxm)p
と表すことができます。fj(p) は p ごとに定まる実数です。これをM上の各点p∈Mで考えることで,1次微分形式の局所座標表示となります。
|
定義 ωの局所座標表示 多様体上の開集合 U上の点p の関数として,ω: p → ωp を考えると, ω=f1dx1+f2dx2+…+fmdxm ; ・・・[*] と1次微分形式 ω: p → ωp を表すことができます。これを ( U,x1,x2,…,xm ) に関するωの局所座標表示という。 |
[7] 次に fk の表式を求めましょう。
ω=f1dx1+f2dx2+…+fmdxm
に対して双対関係 [#] を用いて,次の量を計算すると,
| ω | ∂ | =f1 | (dx1) | ∂ | +・・・+fk | (dxk) | ∂ | +・・・+fm | (dxm) | ∂ | ||||||||||||||||
| ∂xk | ∂xk | ∂xk | ∂xk |
=fk ( fk: p→fk(p) ,p∈M)
つまり,ωの k番目の成分が fk であることがわかります。
特に,局所座標が与えられていれば,公式1と同様に,
(df) ∂ (p) = (df)p ∂ p ∂xk ∂xk
= ∂ p (f) ∂xk
= ∂f (p) ・ (省略されたRの基底) ∂xk
したがって,最初と最後の式を比較して,
(df) ∂ = ∂f ∂xk ∂xk
よって,
df= ∂f dxk+ ∂f dx2+・・・+ ∂f dxm ・・・ [**] ∂x1 ∂x2 ∂xm
と初等解析学で見かける全微分を表す等式と同じ等式が得られます。
[1] 多様体M の2つのCr級座標近傍を (Ux,x1,x2,…,xm),(Uy,y1,y2,…,ym) とするとき,Ux∩Uy (≠φ) において,yj を局所座標系(x1,x2,…,xm) の関数と考えると,全微分 dyj は, [**] 式で,f を yj として,
dyj= ∂yj dxk+ ∂yj dx2+・・・+ ∂yj dxm ・・・ (1) ∂x1 ∂x2 ∂xm
すなわち,j=1,2,・・・,m について,
dyj= ∂yj dxk [余接空間の基底変換] ・・・ (2) ∂xk
x,y について対称な関係にあるので,次式も成り立ちます。
dxj= ∂xj dyk [余接空間の基底変換] ・・・ (2)’ ∂yk
[2]
次に基底が変換されたときに成分がどのように変換されるのか調べます。1次形式が
ω=f1dx1+f2dx2 +…+fmdxm= fkdxk ・・・ (3)
と表されているとします。一方,別の座標系では,
ω=g1dy1+g2dy2+…+gmdym= gj dyj
と表されているとします。ここへ dyj として,(2)式を代入すれば,
ω= gj ∂yj dxk ∂xk
= gj ∂yj dxk ∂xk
この式を(3)と比較して,k=1,2,・・・,m について,
fk= ∂yj gj [成分の座標変換] ∂xk
(2)’を利用して,x と y を入れ換えて考えれば,
gk= ∂xj fj [成分の座標変換] ∂yk
も成り立ちます。
以下,メモ書き
多様体の場合と一般相対性理論の基底(座標)変換の比較
| 接ベクトル空間 Tp(M) | 余接ベクトル空間 Tp*(M) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
基底 (dxk)p (=ek) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 接ベクトル場 | 1次微分形式 (余接ベクトル場) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| X = {Xp}p∈M : p → Xp ∈Tp(M) | ω = {ωp}p∈M : p → ωp ∈ Tp*(M) df ={(df)p}p∈M : p → (df)p ∈ Tp*(M) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Xf : p ∈ M → Xp(f) ∈ R f はpの関数 |
ω(X) : p ∈ M → ωp(Xp) ∈ R (df)(X) : p ∈ M → Xp(f) ∈ R |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ω =f1dx1+…+fmdxm
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 数学(多様体)で利用する表記 (緑=反変,赤=共変) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 物理(一般相対性理論)で利用する表記 (添え字の上下,アインシュタインの縮約) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ユークリッド空間との比較 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ベクトル空間 V | 双対空間 V* | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 基底 ej | 基底 ej | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| e'j=pkjek | ej=qkje'k | e'j=qjkek | ej=pjke'k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x'j=qjkxk | xj=pjkx'k | x'j=pkjxk | xj=qkjx'k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X = a1e1+・・・+amem = ω1(X)e1+・・・+ωm(X)em
| ベクトル空間 V | 双対空間 V* | ||
| 基底 ej | 基底 ej | ||
| e'j=pkjek | ej=qkje'k | e'j=qjkek | ej=pjke'k |
| x'j=qjkxk | xj=pjkx'k | x'j=pkjxk | xj=qkjx'k |
表記上の注意
pmn ⇔ ∂xm , qmn ⇔ ∂x'm ∂x'n ∂xn
| x'k ⇒ yk ,および,ej= | ∂ | , | e'k= | ∂ | と書いて, | ||||||
| ∂xj | ∂yk |
ej= ∂x'k e'k ⇔ ∂ = ∂yk ∂ ∂xj ∂xj ∂xj ∂yk
座標変換の式とベクトルの成分とで変数の記号を区別すれば,
x'j= ∂x'j xk ⇔ ηj= ∂yj χk ∂xk ∂xk
と書くこともある。
| ベクトル空間 | ベクトル場 (相対論) | |||||||||||||||
| 座標変換行列 | pmn |
|
||||||||||||||
| 逆行列 | qmn |
|
||||||||||||||
| 基底 | ej |
|
||||||||||||||
| 双対基底 | ek | dxk | ||||||||||||||
| 基底変換 共変的 |
e'j=pkjek |
|
||||||||||||||
| 基底変換 反変的 |
e'j=qjkek |
|
||||||||||||||
| 座標変換 (反変成分) |
x'j=qjkxk |
|
||||||||||||||
| 座標変換 (共変成分) |
x'j=pkjxk |
|