| 1 確率空間 | |
| f-denshi.com 最終更新日:11/05/25 | |
| サイト検索 | |
[1] 確率論,統計学に必要な定義からはじめる。
|
定義 (1) P(A)≧0 A∈F を満たすとき,Pを確率関数,組(Ω,F,P)を確率空間と呼ぶ。 |
はじめてこの定義を読んだ人は,ちんぷんかんぷん,意味不明にちがいない。補足説明が必要であろう。
集合Ωは標本空間とも呼ばれる。また,F とは,Ωの部分集合からなる集合(=集合族)で加法族[#]と呼ばれ,その元A∈F を確率論では事象と呼ぶ。さらにF は,Ωが整数のような離散集合ならば,可算加法族,実数のような連続集合ならばσ加法族と区別して呼ぶこともある。そして,上記のPとF の定義された集合Ωのことを確率空間と呼び,(Ω,F,P)と書くのである。
まだまだ,大変抽象的なので,どの面も等確率で現れる正四面体のサイコロを例にとり,上の定義の意味を具体的に考えてみる。
 ←正四面体のサイコロ,見えない底面が出目 (←透視せよ!)
←正四面体のサイコロ,見えない底面が出目 (←透視せよ!)
正四面体のサイコロの4つの面には1から4までの数字が記されており,振って底面になった数字を出目と考え,1の目が出ることを {1},1か2のいずれかの目が出ることを{1,2} と書くことにすると,
Ω={1,2,3,4} ←4種の出目は標本点ともいい,その全体集合が標本空間
F ={Ai|Ai= φ,{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{2,3,4},{1,3,4},{1,2,4},{1,2,3},{1,2,3,4} } ←Ωの部分集合たち=事象(たち)となる。(このFは可算加法族)
↓確率関数P
P({φ})=0, ←空集合φも都合上入れておくが,あまり気にしなくてよい
P({1})=1/4,
P({2})=1/4,
P({3})=1/4,
P({4})=1/4,
P({1,2})=2/4,
P({1,3})=2/4,
P({1,4})=2/4,
P({2,3})=2/4,
P({2,4})=2/4,
P({3,4})=2/4, ←A={ , }のいずれかの目が出る確率をP({ , })と書く。
P({2,3,4})=3/4, ←P(A)≧0 を満たす。条件(1)
P({1,3,4})=3/4,
P({1,2,4})=3/4,
P({1,2,3})=3/4,
P({1,2,3,4})=1 ←P(Ω)=1。条件(2)
P({2,3,4})=P({2,3})+P({4})
=P({2})+P({3})+P({4}) などが成り立つ ← 条件(3)の確認
ということになる。ここで,{1}のようにそれ以上分解できない事象を根元事象,{1,2}のようにいくつかの根本事象に分解できる事象を複合事象と区別することも覚えておくべし。
以上を念頭にもう一度,「確率空間の定義」を読むと,確率・統計理論の土俵として,(1),(2),(3)がよくできていることがわかると思う。
[2] 確率空間(Ω,F,P)上の確率変数X=X(ω)とは,集合Ωから実数R への写像であって,任意の実数 r に対して次の条件を満たすものをいう。
{ω|X(ω)≦r,ω∈Ω}∈F
(初めて学ぶ方は,確率変数は変数と呼ばれるが実は写像(←可測関数[#]) なんだということくらいで良いでしょう。そして,今後はA∈Fではなく,Xを用いて議論することになる。)
確率変数は,X(ω)の性質によって次の2通りに分類する。
<1.離散的な確率変数>
Xの取りうる値が高々可算個[#]の場合,Xを離散的な確率変数という。(X(ω)をXと略記する。)
X=xiとなる確率(関数),P(X=xi) が f(xi), i=1,2,・・・,n で与えられるとき,f(xi) を(確率)密度関数と呼ぶ。このとき,
f(xi)≧0, f(xi)=1
を満たす。ここで,nは有限でも無限大でもよい。
すべてで4とおりの出目が等確率で現れる正四面体のサイコロの例では,
P(X=1)=P({1})=f(1)=1/4,
P(X=2)=P({2})=f(2)=1/4,
P(X=3)=P({3})=f(3)=1/4,
P(X=4)=P({4})=f(4)=1/4,
のようになる。つまり,離散的な変数に対しては,確率密度関数fと確率関数P(の部分)とは同一視する。ここでは,離散的な確率変数であることを強調するためにxiという記号を使ったが,後ほど示す連続的な確率変数に対する取り扱いと表記上の整合性を持たせるために,xi→x とし,
f(x)=P(X=x)≡P(X≦x)−P(X<x)
のように確率関数を定義してもよい。これも正四面体サイコロで確かめておくと,
f(3)=P(X=3)=P(X≦3)−P(X<3)=3/4−2/4=1/4
f(3.5)=P(X=3.5)=P(X≦3.5)−P(X<3.5)=3/4−3/4=0
などとなる。
[3] さらに,確率変数Xがx以下である確率密度関数(値)を足し合わせて作られる関数F(x)を(累積)分布関数と定義する。
F(x) =P(X≦x)=
Σ xi≦x f(xi)
累積分布関数の性質として,
(1) 0≦F(x)≦1, F(-∞)=0, F(+∞)=1
(2) 任意のx,yに対して,x<y ならば,F(x)≦F(y) [広義増加関数]
(3) 任意のx,任意の正数εに対して,ε→0のとき,F(x)=F(x+ε) [右連続関数]
が成り立つ。
正4面体のサイコロの例で図示しておくと以下のようになる。累積分布関数(1)-(3)については容易に確認できると思う。
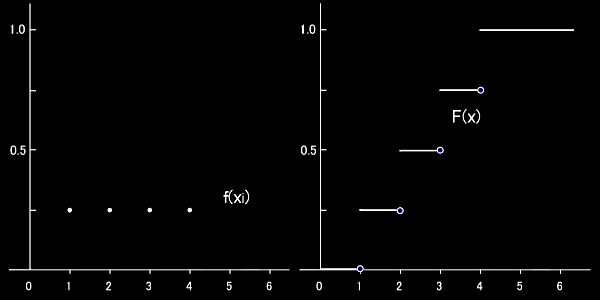
<2.連続的な確率変数>
確率変数Xが実数aとbとの間 (a≦b) にある確率を,P(a≦X≦b) と書くことができ,それがいつも,
P(a≦X≦b)= f(x)dx
で与えられるとき,Xを連続的な確率変数,f(x) を(確率)密度関数と呼ぶ。このとき
f(x)≧0, f(x)dx=1
を満足している。また,確率密度関数f(x)から次のように作られる関数F(x) (=f(x)の原始関数となっている),
F(x) =P(X≦x)= f(t)dt
を(累積)分布関数と呼ぶ。当然ながら,
F'(x)=f(x)
であり,
P(a≦X≦b)= F'(x)dx=F(b)−F(a)
を満足している。
連続的な確率変数が必要とされる問題としては,
「ジロー君が愛用のコーヒーカップを割ってしまうまでの時間X」
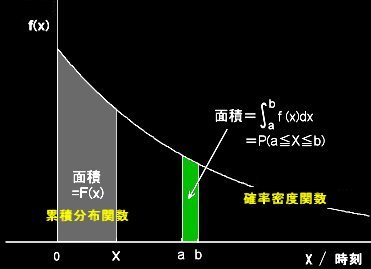
を例としてあげることができる。すなわち,適当な時刻xの関数f(x)が定まり,その関数のaからbまでの定積分(下図の緑色部分の面積)によって,その時刻の間にコーヒーカップが割れる確率を表すことができるのである。(x<0では,f(x)=0と考える。)
 |
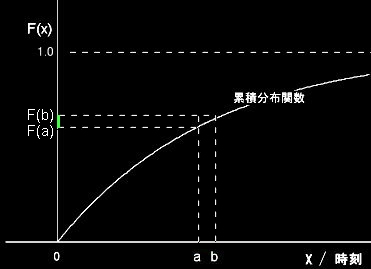 |
上図における区間[0,x]でx軸とf(x)とで囲まれる面積(積分)が累積分布関数F(x)となり,コーヒーカップが時間x以前に割れる確率を意味している。ここで,F'(x)=f(x)。
すると,時刻aとbとの間にコーヒーカップが割れる確率は,
P(a≦X≦b)= F'(x)dx=F(b)−F(a)
と累積分布関数と関係付けられることは容易に確認できるであろう。
補足:ルベーグ積分による確率論とは?
ルベーグ積分を基にしたマッチョな記述だと,例えば,1か2の目が出ることに対応するF の元(事象)は,
{1,2} ⇒ {ω|X(ω)=1∪2,ω∈Ω} ={ω|X(ω)=1または2,ω∈Ω}
のように書くことになる。さらに確率は,
P( {1,2} )=P {ω|X(ω)=1∪2,ω∈Ω}
のように書くべきであろう。
ここで,確率変数Xはωの関数であり,可測関数である。すなわち,その定義,「任意の実数 r に対して次の条件,
{ω|X(ω)≦r,ω∈Ω}∈F
を満たす。これを確かめるには,(条件:ω∈Ωは当たり前なので省略して書くが,)
| {ω∈Ω|X(ω)≦r}= | F | (r≧4) | |
| ω|X(ω)=1},{ω|X(ω)=2},{ω|X(ω)=3}, {ω|X(ω)=1∪2},{ω|X(ω)=1∪3},{ω|X(ω)=2∪3} |
(3≦r<4) | ||
| {ω|X(ω)=1},{ω|X(ω)=2},{ω|X(ω)=1∪2} | (2≦r<3) | ||
| {ω|X(ω)=1} | (1≦r<2) | ||
| φ | (r<1) |
のように場合分けして調べれば,可測関数であることが分かる。
Ωは抽象的な確率変数の定義域であるが,一つの例として長さ1の線分をΩと考えて,4等分し,その領域ωにXを対応させるイメージでもよい。
X(ω)=1 X(ω)=2 X(ω)=3 X(ω)=4
その場合,
P {ω|X(ω)=1∪2,ω∈Ω} =線分の左半分の長さ= 1 2
というように確率変数Xを介して,確率Pとω(線分の長さ)が対応づけられている。ルベーグ積分では確率は確率測度と呼ばれる。
また,ルベーグ積分では確率変数の離散,連続は区別せず,積分記号だけで統一的に表すため,本文中後半の説明は無用となる。しかし,実際の計算ではたいてい場合分けしてコツコツ計算することになるので,ルベーグ積分の”実務上”のご利益はあまりない。だからと言ってルベーグ積分が無意味というわけではない。ルベーグ積分による確率論は,初等解析学では厳密な取り扱いができない中心極限定理のように無限集合の収束を議論するとき,威力を発揮する。
サイコロを n回投げるときは,ωをn次元ベクトル(ω1,ω2,・・・,ωn)∈Ω と考えればよい。k回目の出目を表す確率関数は,
Xk(ω)=X(ωk)
のように定義すればよいだろう。各ωkは上に示した1本の4等分線にそれぞれ対応している。つまり,Ωを構成するためにはn次元の1辺が4等分された立方体が必要となる。
1回目が1,2回目が3が出る確率は,
P {ω|X1(ω)=1,X2(ω)=3,ω∈Ω}
と表す。