とファトゥの補題
| 7 上・下極限集合 とファトゥの補題 |
||
| f-denshi.com [目次へ] 最終更新日:16/08/02 間違い修正 | ||
| サイト検索 | ||
[1] 実数の数列と同じように集合列というものを考えることができます。まず,単調増加列とは,
A1 ⊂ A2 ⊂ ・・・・ ⊂ An ⊂ ・・・・
となる集合列で,その極限を,
An ≡ An
と定義します。また,単調減少列は,
A1 ⊃ A2 ⊃ ・・・・ ⊃ An ⊃ ・・・・
であって,その極限を,
An ≡ An
と定義します。
[2] 一般的な収束列は,増加列でも減少列でもなく,例えば,
Ak = { (x,y)|x2 + y2 ≦( 1−(-1)k/k)2 }
ならば,半径が 1−(-1)k/k の円の内部とその円周に属する点の集合を第 k 列目の集合 Ak とする場合,”増・減” を繰り返しながら収束していくように見える場合があります。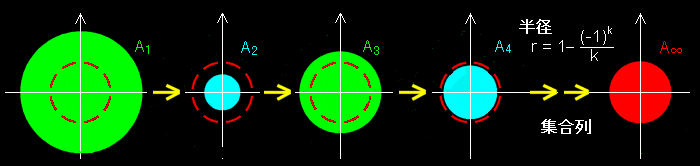
このような場合に有効なのが,上極限集合,下極限集合,
定義
lim Ak≡ limsup Ak ≡ Ak ←上極限集合
lim An ≡ liminf Ak ≡ Ak ←下極限集合
であって,数列の上極限,下極限に相当します。今の例で,上極限集合,下極限集合への収束の様子を図示すると,下のようになります。
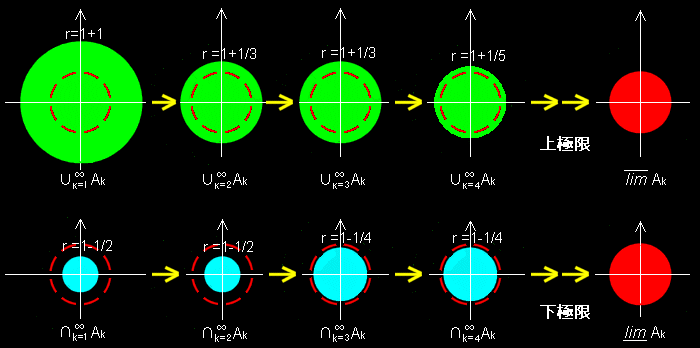
この場合,上極限集合,下極限集合とは同じ集合,半径 1 の円の内部と周囲からなる集合へ収束しており,このようなとき,集合列は収束すると言います。
正しくは,
上極限集合は, x2+y2≦1
下極限集合は, x2+y2<1
となるので,この集合列は収束しない。 一般的に liminf Ak ⊂ limsup Ak
というのが正しいです。 ↑ 高橋jon助 様からご指摘いただきました。m(..)m
無限個の閉集合の共通部分は閉集合とはならない!
But 面積(測度)は等しい。
一般的に, m ( liminf Ak) ≦ m ( limsup Ak)
[3] 以上の記法を用いて,可測集合の集合列とその測度に成り立つ関係を述べておくと,
|
命題1 測度空間 (X,β,m ) が与えられ,Ak∈β,k=1,2,・・・ とするとき, が成り立つ。ただし,A1<∞ とする。 (3)と(4)をまとめて,単調増加列 { Ak },及び, A1<∞ なる単調減少列 { Ak } に対して,
|
||||||||||||||||||||||||||||||||||
証明
(1) 証明済み ⇒ [#]
(2) σ集合体の性質を用いれば,
liminf Ak ≡ Ak
| において,Ak∈βならば, | Ak≡Cn∈β。 さらに,Cn∈βならば, |
liminf Ak ≡ Cn ∈β
limsup の方も liminf と同様に証明できる。
すなわち,「可測集合は可算個の共通部分集合や下極限集合,上極限集合を考えてもはみだすことはない」ということです。
(3) 単調増加列 {An}から,
Bn=An∩An-1c=An−An-1 (B1=A1) を作れば,
Bk= Ak =An n=1,2,・・・・,∞
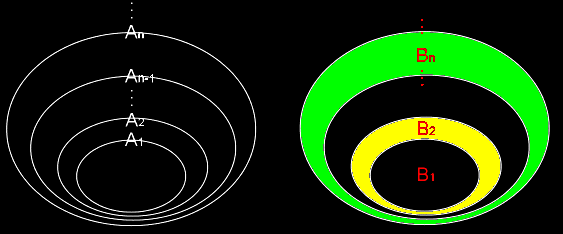
であり,さらに,Bnは互いに素である。したがって,測度の定義より,
m( Ak)= m ( Ak )
=m ( Bk ) = m(Bk)
= m(Bk)= m ( Bk )
= m ( Ak ) = m ( An )
= m ( Ak )
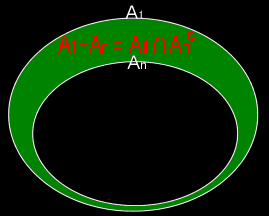
(4) Akが単調減少列のとき,
Cn=A1∩Anc=A1−An とすれば,Cnは単調増加なので,(3)の結果を適用して,
m(Ck) =m( Ck)≡m( Ck ) ・・・(0)
ところが,(0)の左辺は,
m(Ck) =m(A1)− m(Ak) ・・・(1)
一方,(0)の右辺(中央)は分配法則,ド・モルガンの法則: Pc∪Qc=(P∩Q)c を用いて,
m( Ck)=m( (A1∩Akc) )
=m( A1∩( Akc ) )=m( A1∩( Ak)c )
=m(A1− Ak )=m(A1)−m( Ak) ・・・(2)
(1)と(2)を等値すれば,m(A1) (<∞として) がキャンセルされて,
m(Ak) =m( Ak)=m( An )
と証明すべき式が得られる。
[2] 測度空間 X(β,m ) が与えられたとき[#],
命題2
(任意の)集合列 { Ak }に対して,
m( Ak) ≦ m(Ak)
もし,集合が図形で,m がその面積であれば,この命題の意味は,これまで何回も述べてきた(カラテオドリの外測度)[#] 直感的にごく当たり前なことを述べているので問題ないはず。
|
ファトゥーの補題 であるならば, 書き直して, が成り立つ。 (k→∞ の記号は省略してもよい。) |
これより,集合列 { Ak } が収束すれば,すべての等号が成り立つ,すなわち,
m(Ak) =
lim m(Ak) =
lim m(Ak)
が存在すること,および,
m(Ak) = m( Ak)
が成り立つことが示されます。
ファトゥーの補題の証明 ↓ 1.の命題1 [#] を使います。
| (左) Bn = | Ak とおくと,Bn⊂An であり, | |||
m(Bn)≦m(An)
また,Bnは増加列であり,
Bk= Bn = Ak =
lim Ak
したがって,
m(
lim Ak ) =m( Bk) = m(Bk) ←命題1の(3)を用いた
さらに,増加列の極限は下極限と同じなので,
= m(Bk) =
lim m(Bk)≦
lim m(Ak)
以上で,[*]式の左の不等式≦が証明された。
| (右) 今度は, Cn = | Ak とおくと,An⊂Cn であり, | |||
m(An)≦m(Cn)
また,Cnは減少列であり,・・・・ と以下,(左)の場合と同様な(∪∩は反対になるが)議論を行えば,
命題1の(4)を用いて,右の不等式≦が証明できる。
(中) 中央の不等式については,実数 (測度は実数) に対する上極限と下極限に対して成り立つ関係なので自明。
結局,[*]のすべての不等式が成り立つことが分かった。